A long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (c ) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (d) What is the velocity of this particle at this instant ?
10√2πcm/s
40√2πcm/s
30√2πcm/s
20√2πcm/s
Mass per unit length of the string is
μ=Ad=(0.80mm2)×(12.5g/cm3)=0.01kg/m
=(0.80×10−6m2)×(12.5×103)=0.01kg/m
speed of transverse waves produced in the string
v=√Tμ=√640.01kg/m=80m/s
the amplitude of the source is a=1.0cm and the frequency is f=20Hz. the angular frequency is ω=2πf=40π/s.
also at t=0, the displacement is equal to its amplitute, i.e., at t=0,y=a. the equation of motion of the source is, therefore,
y=(1.0cm)cos[(40πs−1)t] ...(1)
the equation of the wave travelling on the string along the positive X−axis is obtained by replacing t by [t−(x/v)] in Eq. (i). It is, therefore,
y=(1.0cm)cos[940πs−1){t−(x/v)}x]
=(1.0cm)cos[(40πs−1)t−{(π/2)m−1)}x]
the displacement of the particle at x=50cm at time t=0.05s is obtained from Eq. (ii).
y=(1.0cm)cos[(40πs−1)(0.05s)
−{(π/2)m−1(0.5m)]
=(1.0cm)cos[2π−(π/4)]
=1.0cm/√2=0.71cm
the velocity of the particle at position x at time t is also obtained from Eq. (ii).
V=∂y∂t=−(1.0cm)(40πs−1)t−{(π/2)m−1}x]
=−(40πcms)sin(2π−π4)
=−40π√2cm/s=−89cm/s
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Assertion-Reasoning
Explore 6 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICSChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A uniform string of length 6.5m is subjected to a tension of 40N. Mass of the string is 162.5g. One end of the string is fixed and the other end is tied to a source (s). which produces a transverse oscillation. The displacement of the end of the string tied to the source can be expressed as y=(3mm)sin(40πt), where ‘t’ is time. Find the displacement of point P of the string at a distance of 3.75m from the fixed end, at time t=0.3s.

View SolutionA String on a cello vibrates in its first normal mode with a frequency of 220Hz. The vibrating segment is 70.0cm long and has a mass of 1.20g . (a) Find the tension in the string . (b) Determine the frequency of vibration when the string vibrates in three segments .
View Solution
Knowledge Check
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
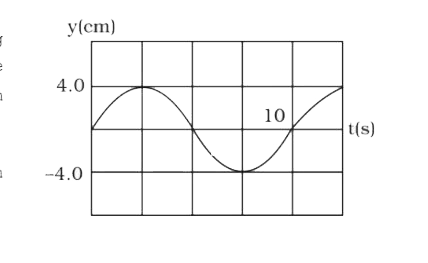
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?A−2cm/sB+2cm/sC+1.5cm/sD−2.5cm/sThe displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
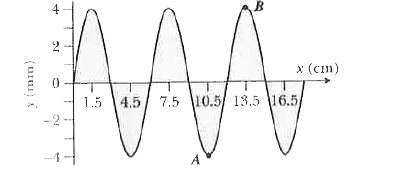
What is the wavelength of the wave?A3.0 cmB6.0 cmC9.0 cmD12 cmThe displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
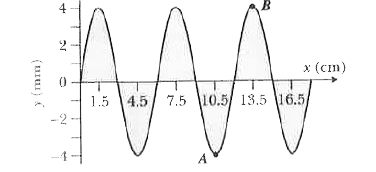
What is the frequency of the wave?A0.60HzB0.90HzC1.7HzD1.3Hz
A string 1 m long with mass 0.1 g cm−1 is under a tension of 400 N.Find is fundamental frequency of vibration.
View SolutionThe equation for a wave travelling in x-direction 0n a string is
y=(3.0cm)sin[(3.14cm−1x−(314s−1t]
(a) Find the maximum velocity of a particle of the string.
(b) Find the acceleration of a particle at x=6.0cm at time t=0.11s
View SolutionThe displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
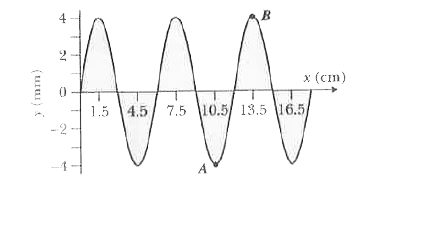
What is the amplitude of the wave?
View SolutionA string of length 0.5m and linear density 10−4 kg/m is stretched under a tension of 100 N. If the frequency of the vibration of the string is 4000 Hz, how many loops are formed on the string?
View SolutionA string of density 7.5gcm−3 and area of cross section 0.2mm2 is stretched under a tension of 20 N. When it is plucked at the mid point, the speed of the transverse waves on the wire is
View Solution

