If the maximum speed of a particle on a travelling wave is v0, then find the speed of a particle when the displacement is half of the maximum value.
v02
√3v04
√3v02
v0
The correct Answer is:c
For the wave y=Asin(ωt−kx),v0=Aω
where A is, the maximum displacement.for the given condition,
A2=Asin(ωt−kx)
sin(ωt−kx)=12
And ∂y∂t=Aωcos(ωt−kx)=Aω√32=√3v02
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Single Correct Answer
Explore 1 Video
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Multiple Correct
Explore 25 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Subjective
Explore 16 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICSChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
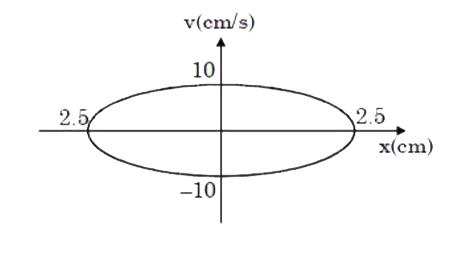
View SolutionDisplacement (S) of a particle is given as S=(t3–t2). Find the speed of the particle when it's acceleration is zero
View Solution
Knowledge Check
The maximum speed of a particle in SHM is given by mA=Vm. The average speed of the particle in terms of maximum speed is given by
AVm2BπVm2C2VmπDπ2VmMaximum speed of a particle in simple harmonic motion is vmax. Then average speed of this particle in one time period is equal to
Avmax2BvmaxπCπvmax2D2vmaxπMaximum speed of a particle in simple haromonic motion is vmax. Then average speed of a particle in one complete oscillation is equal to
Avmax2BvmaxπCπvmax2D2vmaxπ
In above question 1, find the speed of each speed of each particle, when the separation reduces to half its initial value
View SolutionA particle travels half of the circle of radius r. Then the displacement and distance of the particle are respectively.
View SolutionVelocity of a particle in stationary wave is maximum at
View SolutionA transverse wave passes through a medium, the maximum speed of the vibrating particle when the displacement of the particle from the mean position is
View SolutionThe displacement of a particle executing SHM is given by y=0.5 sint cm . The maximum speed of the particle is
View Solution

