In above question 1, find the speed of each speed of each particle, when the separation reduces to half its initial value
√Gmd
√2Gmd
√Gm2d
None of these
The correct Answer is:A
Increase in kinetic energy of both particles = decrease in gravitational potential energy
∴2(12mv2)=Ui=Uf=−Gmmd+Gmmd2=Gm2d
∴v=√Gmd.
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.5
Explore 20 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.6
Explore 20 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:Check Point 10.3
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEYChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
Similar Questions
Find out speed of particles when separation between them is r.

View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
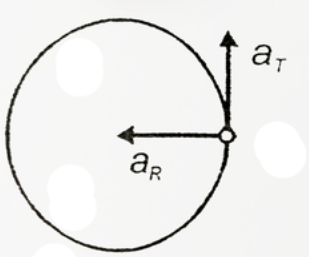
The time after which the speed of particle reduces to half of its initial value is
View Solution
Knowledge Check
In the above question, the speed of the particle at origin will be:
A10√2msB1.5msC10msDnone of theseIf the maximum speed of a particle on a travelling wave is v0, then find the speed of a particle when the displacement is half of the maximum value.
Av02B√3v04C√3v02Dv0A particle starts moving in a straight line with initial velocity v0 Applied forces cases a retardation of av, where v is magnitude of instantaneous velocity and α is a constant.
How long the particle will take to reduce its speed to half of its initial value?Ain2αBα In 2C1αDinfinite
Two point objects of masses 10 g each carry charges of opposite nature with the same magnitude of 50 μC are held at rest at a separation of 2 m. Now the point objects are released from the state of rest. Calculate the speed acquired by both the objects when separation between them reduces to half of the initial value.
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of +4.0×10−5C. They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionIn above question, what will be the speed of the particle on the ring which is at the same height as that of the centre?
View SolutionIn the above question, the speed of each ball relative to ground just after they leave the disc is -
View SolutionIn one half- life time duration
activity of a sample reduced to half of its initial value.
total number of nuclei present are reduced to half of its initial value.
number of radioactive nuclei present is reduced to half of its initial value
mass of sample is reduced to half of its initial value
Out of these, correct statements are
View Solution

