A stationary observer receives sound waves from tow tuning forks, one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears beats of frequency υ=2Hz. Find the velocity of each tuning fork if their oscillation frequency is υ0=680Hz and the velocity of sound in air is υs=340ms.
n'=c−v0c−vS×n
Here
n'=340−0340−v×680=340340−v×680
n''=340−0340+v×680=340340+v×680
Now n'−n''=
or 340×680(2v3402−v2)=2
or v=340680=0.5ms
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Subjective
Explore 56 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Single Correct
Explore 252 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Exercise 6.1
Explore 56 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Comprehension Type
Explore 5 Videos
Similar Questions
A stationary observer receives sonic oscillations from two tuning forks one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears the beats of frequency f=2.0HZ. Find the velocity of each tuning fork if their oscillation frequency is fo=680HZ and the velocity of sound in air is υ=340m/s.
View SolutionA stationary observer receives sound from two indentical tuning forks, one of which approaches and the other one recedes with the same speex (much less than the speed of sound). The observer hears 2 beats/ sec. The oscillation frequency of each tuning fork is v0=1400 Hz and the velocity of sound in air is 350 m/s. The speed of each tuning fork is close to :
View Solution
Knowledge Check
With what velocity should you approach tuning fork of frequency 256 Hz so that the apparent frequency is 512 Hz. Velocity of sound in air is 340 m/s
A340 m/sB320 m/sC260 m/sD540 m/sDistance travelled by the sound produced by a tuning fork of frequency 50 Hz completing 200 vibrations is, (the velocity of sound in air is 330 m/s)
A1100 mB3300 mC660 mD1320 mTwo tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
A1.5 m/sB2 m/sC1 m/sD2.5 m/s
Two tuning forks with natural frequencies of 340 Hz move relative to a stationary oberserver. One fork moves away from the obsorver, while the other mover towards at the same speed. The observer hears beats of freqeuency 3 Hz. Find the speed of the tuning forks assuming the velocity of sound in air to be 340 m/s.
View SolutionTwo tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
View SolutionTwo tuning forks are vibrating with natural frequency of 510 Hz . One tuning fork moves away from the stationary observer, while the other moves towards him at the same speed. The observer hears beats of frequency 6 Hz. The speed of each tuning fork is -- m/s. (speed of sound in air = 340m/s)
View SolutionHow far does the sound travel in air, when a tuning fork of frequency 256 Hz makes 32 vibrations? Velocity of sound in air =320m/s.
View Solution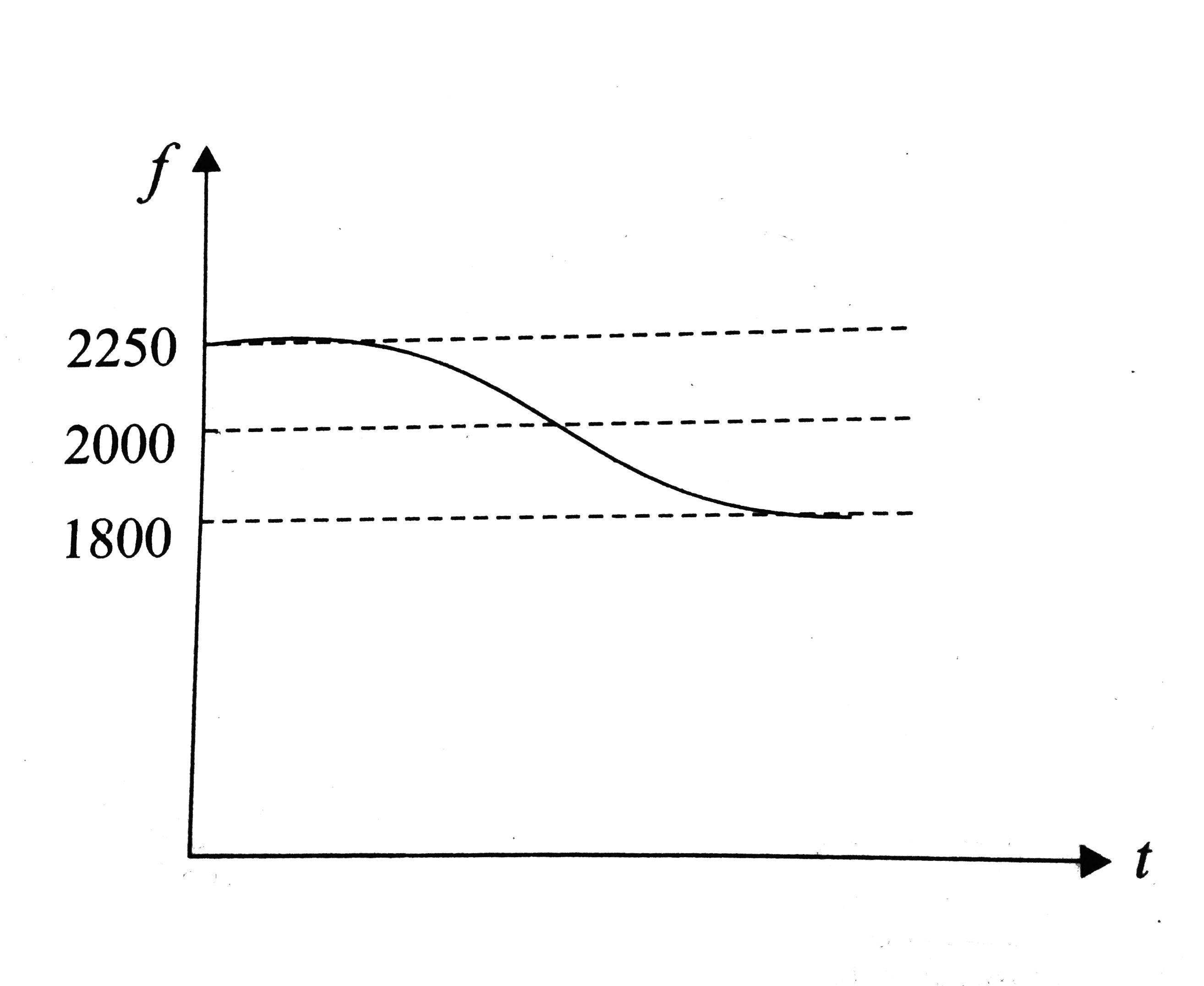
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View Solution

