In the previous problem, if O is the point on AD and OO1 is the perpendicular from the centre of the circle, O−1,thenOA/OD will be
A
1
B
>1
C
<1
D
depands upon →B and charge
Video Solution
Text Solution
The correct Answer is:A
O will be the midpoint of incident and point of emergence . Hence, OA=OB.
|
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
In previous problem the acceleration o fbolck is.
AzeroB10m/s2 upwardC10m/s2 downwardDnone of theseIn the adjacent figure AD is a straight line. OP is perpendicular to AD and O is centre of both circles. If OA=20 cm, OB=15 cm and OP=12 cm then what is the length of AB?
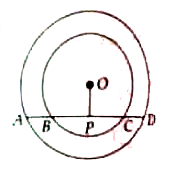 AA)7 cmBB)8 cmCC)10 cmDD)12 cm
AA)7 cmBB)8 cmCC)10 cmDD)12 cmIn the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cm
If figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

View SolutionTwo tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionIf OA=12 cm, then find the length of PQ (in cm), where O is the centre of circle.

View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
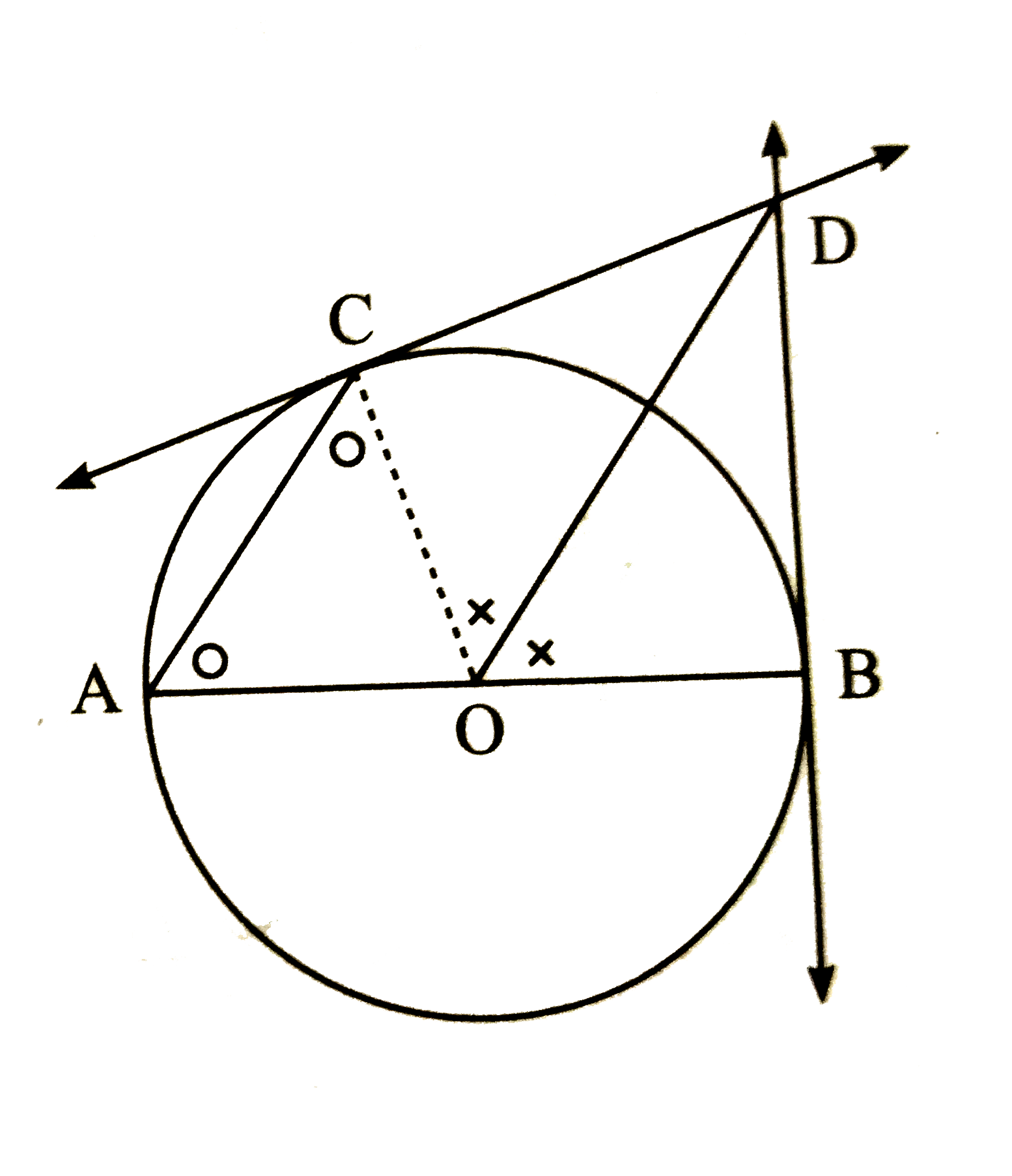
View Solution