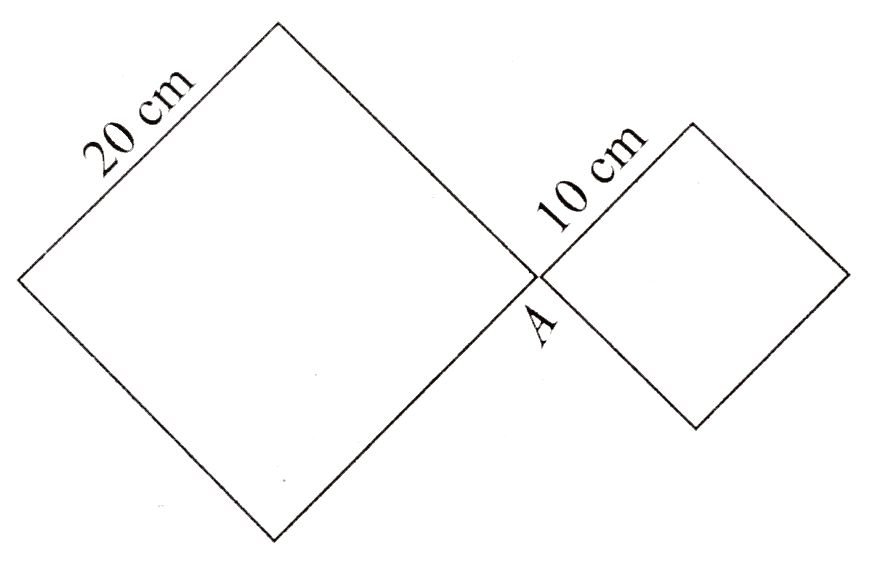
A plane loop is shaped as two squares (Fig) and placed in a uniform magnetic field at right angle to the loop's plane. The magnetic induction varies with time as B=B0sin(ω)t,whereB0=10mTand(ω)=100rads−1. The wires do not touch at point A. If resistance per unit length of the loop is 50m(Ω)/m, then amplitude of current induced in the loop is
1.5A
1.0A
0.5A
2.0A
The correct Answer is:C
Induced emf's in the two loops will oppose each other. So net induced emf:
e=ddt[(b2−a2)B]=(b2−a2)dBdt
=(0.202−0.102)(ωB0cos(ω)t
=(0.04−0.01)×100×10×10−3cos(ω)t
=30×10−3cos(ω)t
Resistance : R=50×10−3[4×20+4×10]=60×10−3(Ω)
I=eR0.5(ω)t
so aamplitude of current =0.5A.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
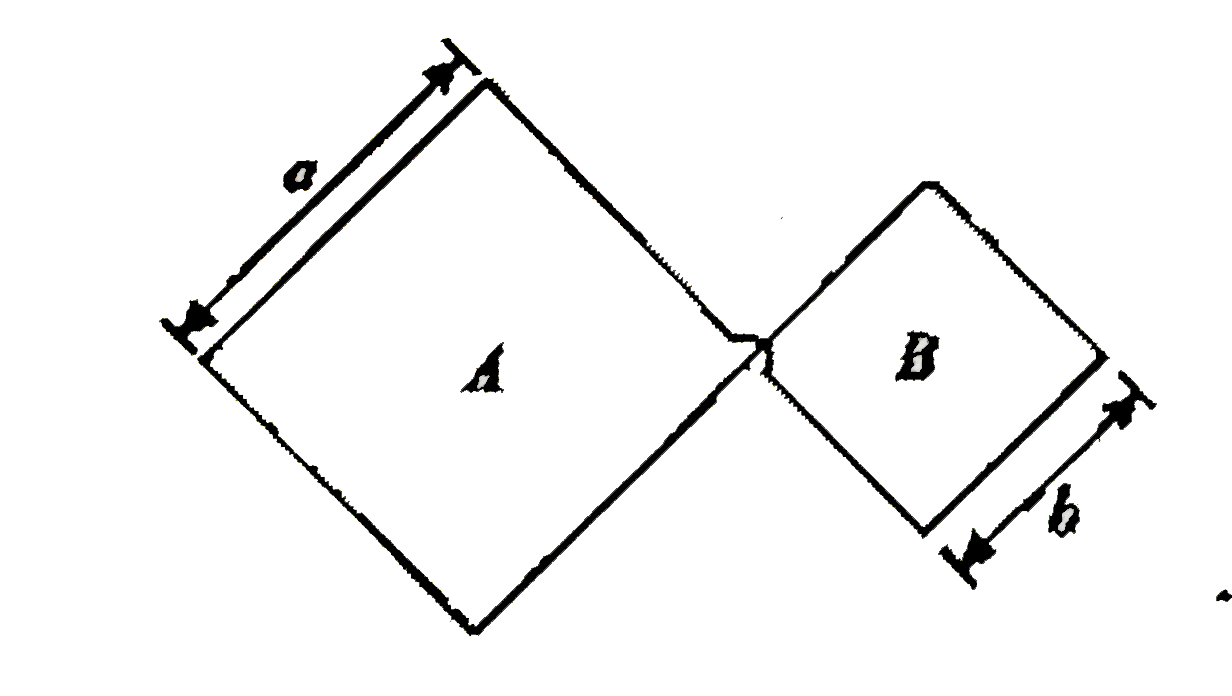
A plane loop shown in figure-5.71 is shaped in the from of two squares with sides a and b and it is introduced into a uniform magnetic field at right angles, to the loop's plane. The magnetic induction varies with time as B=B0sinωt. find the amplitude of the current induced in the loop if its resistance per unit length is equal to r. the induction of the loop is negligible.
View SolutionA conducting loop of area A is placed in a magnetic field which varies sinusoidally with time as B=B0sin
View Solution
Knowledge Check
A plane loop, shaped as two squares of sides a=1m and b=0.4m is introduced into a uniform magnetic field ⊥ to the plane of loop . The magnetic field varies as B=10(−3)sin(100t)T. The qamplitude of the current induced in the loop if its resistance per unit length is r=5mΩm−1 is
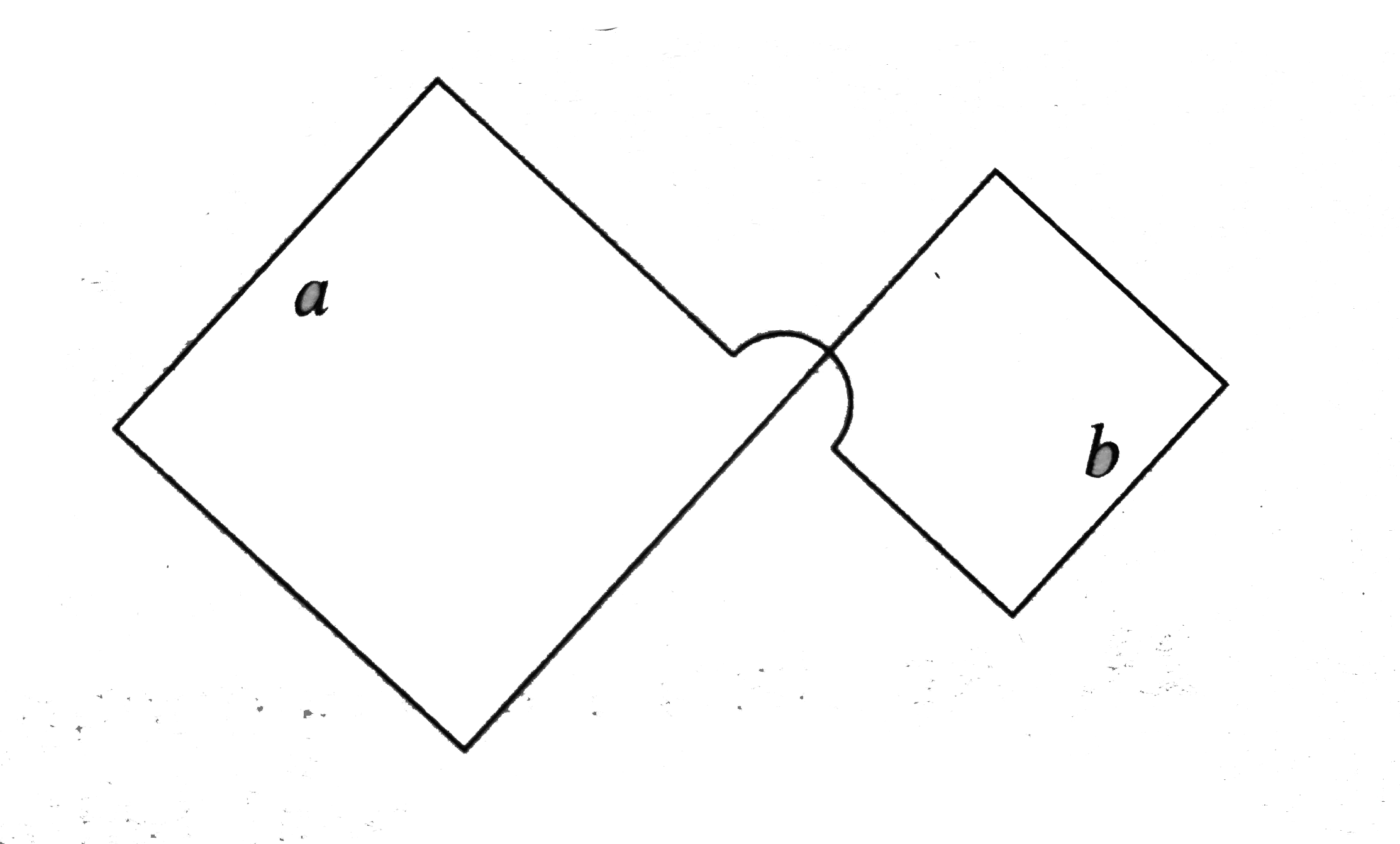 A(a) 2AB(b) 3AC( c) 4AD(d) 5A
A(a) 2AB(b) 3AC( c) 4AD(d) 5AA triangular loop of side 1 carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
AlBlBzeroCl2BlDinfinityA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A plane spiral with a great number N of turns wound tightly to one another is located in a uniform magnetic field perpendicular to the spiral's plane.The outside radius of the spiral's turns is equal to a and inner radius is zero.The magnetic induction varies with time as B=B0sinωt, where B0 and ω are constants.The amplitude of emf induced in the spiral is εim=1xπa2NωB0.Find out value of x.
View SolutionA current loop of arbitrary shape lien in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View SolutionA circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View Solution
