A stsnding wave is set up in the wire fixed at both ends by two vertical walls (see Fig. 3.197). The region between the walls contains a constant magnetic field . Now answer the following question:

In the above qestion, the time when the emf becomes maximum for the time is
(a)
(b)
( c)
(d)
The correct Answer is:C
( c)
For second harmonic
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A standing wave y=2Asinkxcosωt is setup in the wire AB fixed at both ends by two vertical walls (see the figure). the region between the wall contains a constant magnetic field B. Now answer the following questions.
In the above question, the time when the emf becomes maximum for the first time is
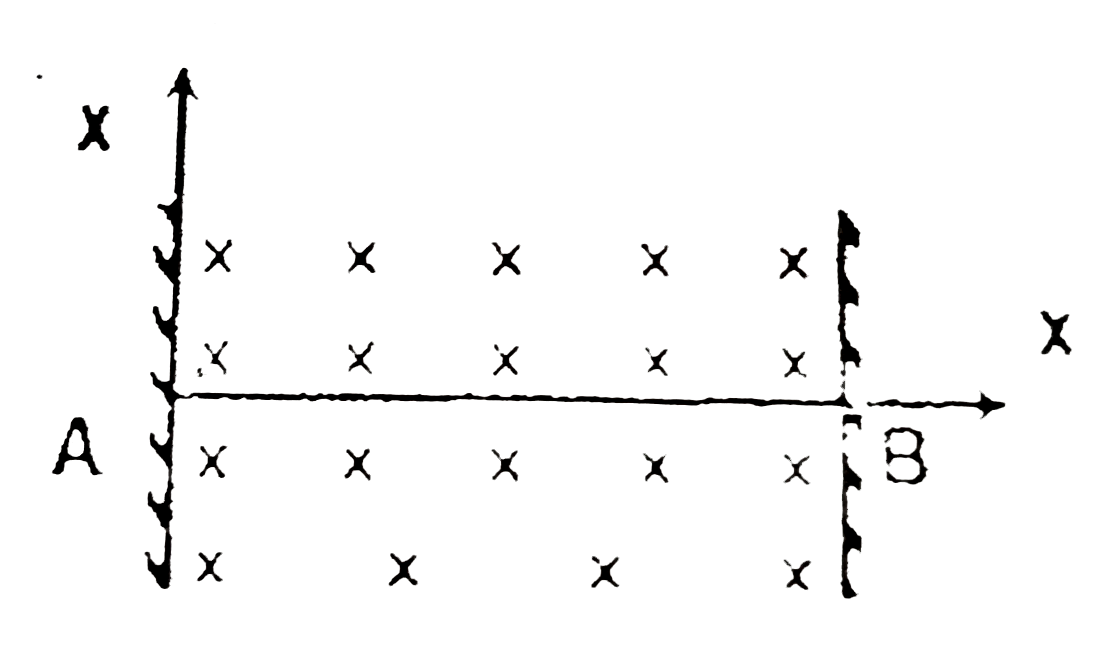
View SolutionA standing wave y=Asinkx.cosωt is established in a string fixed at its ends.
(a) What is value of instantaneous power transfer at a cross section of the string when the string is passing through its mean position?
(b) What is value of instantaneous power transfer at a cross section of the string when the string is at its extreme position?
(c) At what frequency is the power transmitted through a cross section changing with time?
View Solution
Knowledge Check
A standing wave y=2Asinkxcosωt is set up in the wire AB fixed at both ends by two vertical walls (see Fig. 3.197). The region between the walls contains a constant magnetic field B. Now answer the following question:

The wire is found to vibrate in the third harmonic. The maximum emf induced isA(a) 4(AB)ωkB(b) 3(AB)ωkC( c) 2(AB)ωkD(d) ABωkA stsnding wave y=2Asinkxcosωt is set up in the wire AB fixed at both ends by two vertical walls (see Fig. 3.197). The region between the walls contains a constant magnetic field B. Now answer the following question:

In which of the following modes the emf induced in AB is always zero?A(a) fundamental modesB(b) second harmonicC( c) ssecond overtoneD(d) fourth overtoneEstimation of frequency of a wave forming a standing wave represented by y=Asinkxcost can be done if the speed and wavelength are known using speed=Frequency×wavelength . Speed of motion depends on the medium properties namely tension in string and mass per unit length of string . A string may vibrate with different frequencies . The corresponding wavelength should be related to the length of the string by a whole number for a string fixed at both ends . Answer the following questions:
If y=10sin5xcos2tm represents a stationary wave then , the possible one of the travelling waves causing this isAy=10sin(5x−2t)By=5sin(2t−5x)Cy=10sin2tDy=5cos5x
(i) The equation of wave in a string fixed at both end is y=2sinπtcosπx. Find the phase difference between oscillations of two points located at x=0.4m and x=0.6m.
(ii) A string having length L is under tension with both the ends free to move. Standing wave is set in the string and the shape of the string at time t=0 is as shown in the figure. Both ends are at extreme. The string is back in the same shape after regular intervals of time equal to T and the maximum displacement of the free ends at any instant is A. Write the equation of the standing wave.

View SolutionEstimation of frequency of a wave forming a standing wave represented by y=Asinkxcost can be done if the speed and wavelength are known using speed=Frequency×wavelength . Speed of motion depends on the medium properties namely tension in string and mass per unit length of string . A string may vibrate with different frequencies . The corresponding wavelength should be related to the length of the string by a whole number for a string fixed at both ends . Answer the following questions:
A string fixed at both ends having a third overtone frequency of 200Hz while carrying a wave at a speed of 30ms−1 has a length of
View SolutionA thin non-conducting ring mass m, radius a, carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment the ring was at rest and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downwards and increase with time according to the law B=B0t. Neglecting magnetism induced due to totational motion of the ring. Now answer the following questions.
The angular acceleration of the ring and its direction of rotation as seen from above: if E is induced e.m.f
View SolutionIn YDSE set up (see fig.), the light sources executes SHM between P and Q according to the equation x=Asinωt, S being the mean position. Assume d→0 and A<<L. ω is small enough to neglect Doppler effect. If the sources were stationary at S, intenstiy at O would be I0
Read the paragraph carefully and answer the following questions.
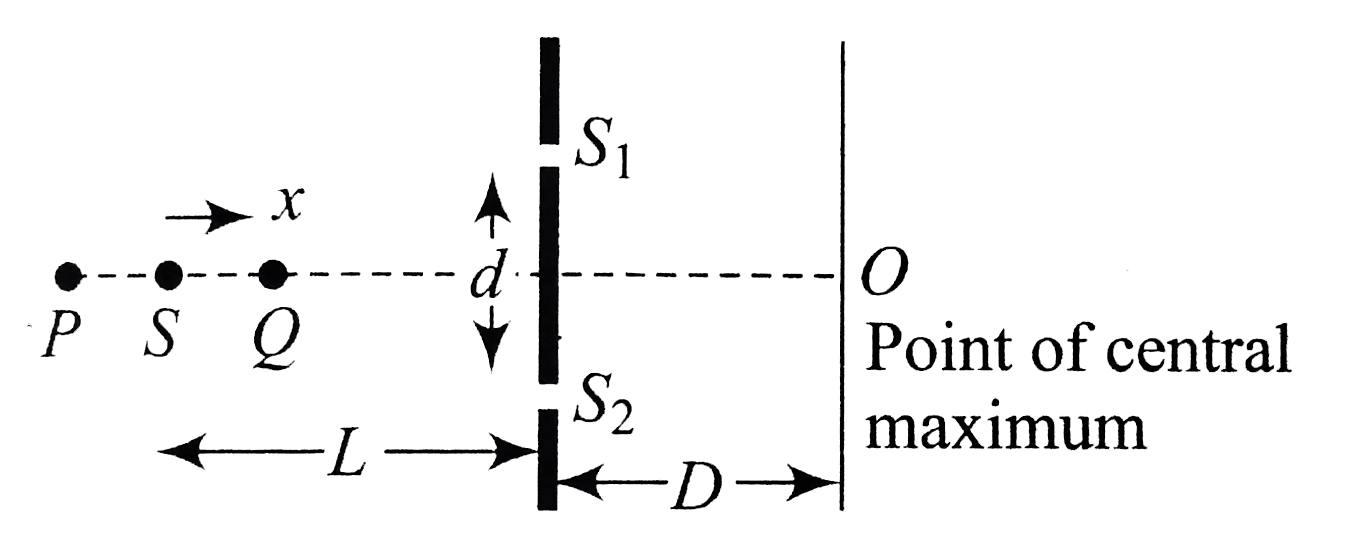
The fractional change in intensity of the central maximum as function of time is
View SolutionThere are two infinite parallel current carrying wires in vertical plane. Lower wire is fixed and upper wire is having a linear mass density λ. Two wires are carrying currents I1 and I2. Now upper wire is placed in a magnetic field produced by lower wire. Magnetic field due to lower wire at the location of upper wire is μ0I2πd, where I1 current lower wire, d separation between wires.
Force on any small portion of upper wire having length dl is dF=μ0I1I2dl2πd, where I2 current in the upper wire. If directions of current in the wires is appropriate then upper wire can be in equilibrium if its weight is balanced by magnetic force. Now answer the following questions.
If upper wire is slightly displaced from its mean position and released it will perform simple harmonic motion. As wire then total mechanical energy of wire
View Solution
