A thin non-conducting ring of mass m carrying a charge q can freely rotate about its axis. At t=0, the ring was at rest and no magnetic field was present. Then suddenly a magnetic field B was set perpendicular to the plane. Find the angular velocity acquired by the ring.
Due to the sudden chrage in flux, an electirc field is set up and the ring experiences an impulsive torque and suddenly acquires an angular velocity.
E=r2dBdt
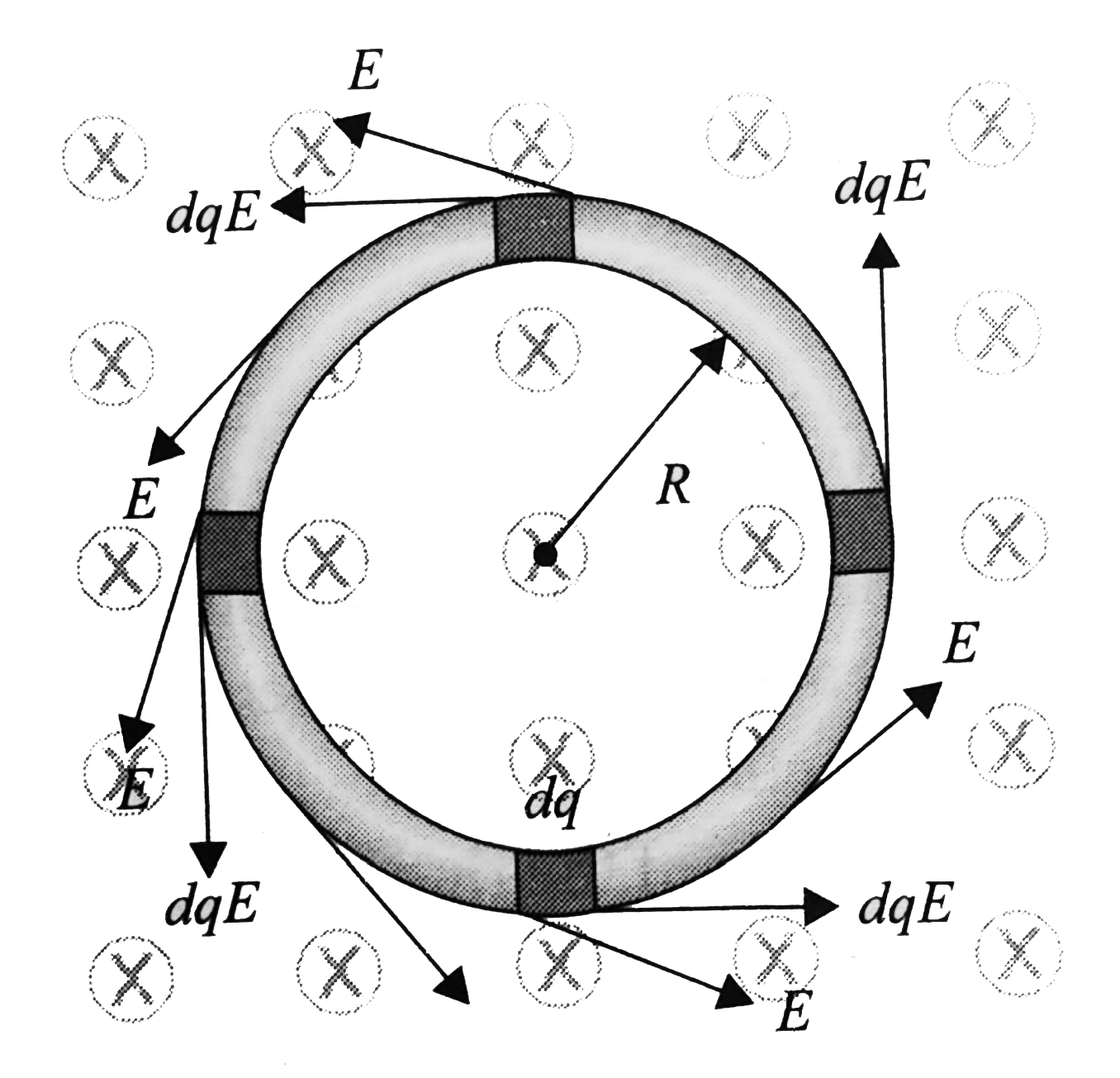
Force experiences by an element of ring dF=dqE
Torque experiences by this element of ring dtau=dFr=dqEr
Total torque experienced by ring: τ=qEr
angular impulse experienced
L=∫τdt=qr22∫dBdtdt=qr22B
L=Iω → mr2ω=qr22B → ω=qB2m
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A thin non-conducting ring of mass m carrying a charge q can freely rotate about its axis. At the initial moment, the ring was at rest and no magnetic field was present. Then a uniform magnetic field was switched on, which was perpendicular to the plane of the ring and increased with time according to a certain law: dBdt=k.
Find the angular velocity ω of the ring as a function of k.
View SolutionA thin non-conducting ring of mass m carrying a charge q can freely rotate about its axis. At the initial moment the ring was at rest and no magnetic field was present. Then a practically unifrom magnetic field was switched on, which was perpendicular to the planeof the ring and increased with time according to a certain law B(t), Find the angluar velocity ω of the ring as a function of the induction B(t).
View Solution
Knowledge Check
A thin non-conducting ring mass m, radius a, carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment the ring was at rest and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downwards and increase with time according to the law B=B0t. Neglecting magnetism induced due to totational motion of the ring. Now answer the following questions.
The power developed by the forces acting on the ring, as a function of time :AE2q22mtBE2q2mtC2E2q2mtD√2E2q2mtA thin non-conducting ring mass m, radius a, carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment the ring was at rest and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downwards and increase with time according to the law B=B0t. Neglecting magnetism induced due to totational motion of the ring. Now answer the following questions.
The angular acceleration of the ring and its direction of rotation as seen from above: if E is induced e.m.fAEq2ma, anticlockwiseBEqma, anticlockwiseC2Eqma, clockwiseDEqma clockwiseA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Find intantaneous power developed by electric force acting on the ring at t=1sA2q2B20a214mBq2B20a28mC3q2B20a2mDq2B20a24m
A thin non conducting horizontal disc of mass m having total charge q distributed uniformly over its surface, can rotate freely about its own axis. Initially when the disc is stationery a magnetic field B directed perpendicular to the plane is switched on at t=0. Find the angular velocity ω acquired by disc as a function of time, if B=kt, where t is time.
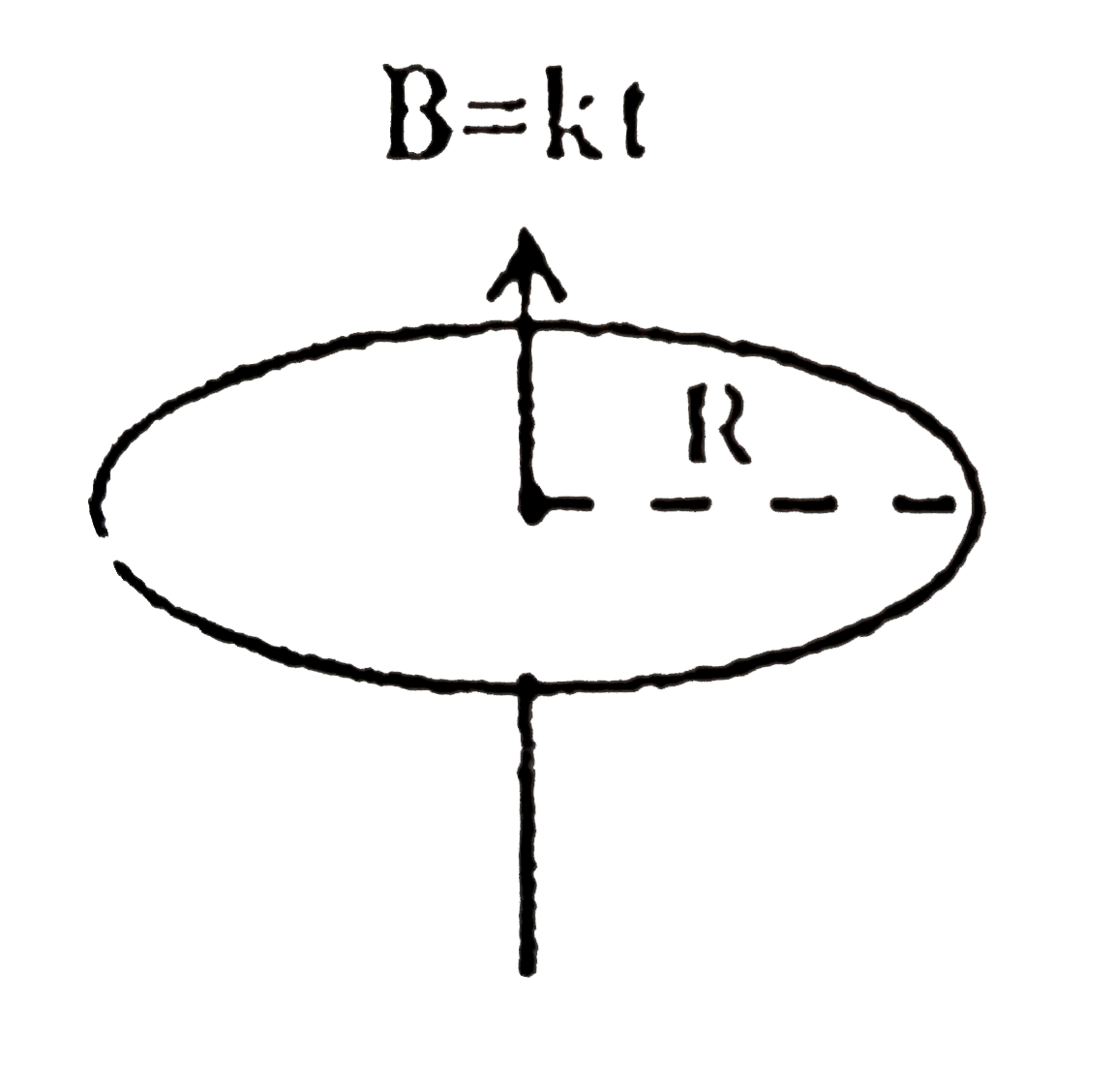
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Angular acceleration of ring is
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
The magnitude of an electric field on the circumference of the ring is
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
The magnitude of induced emf of the closed surface of ring will be
View SolutionA ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is:
View Solution
