There exists a long conductor along z-axis carrying a current I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference VBA=V is applied. Radii of arcs are a and b, respectively, as shown in the figure.
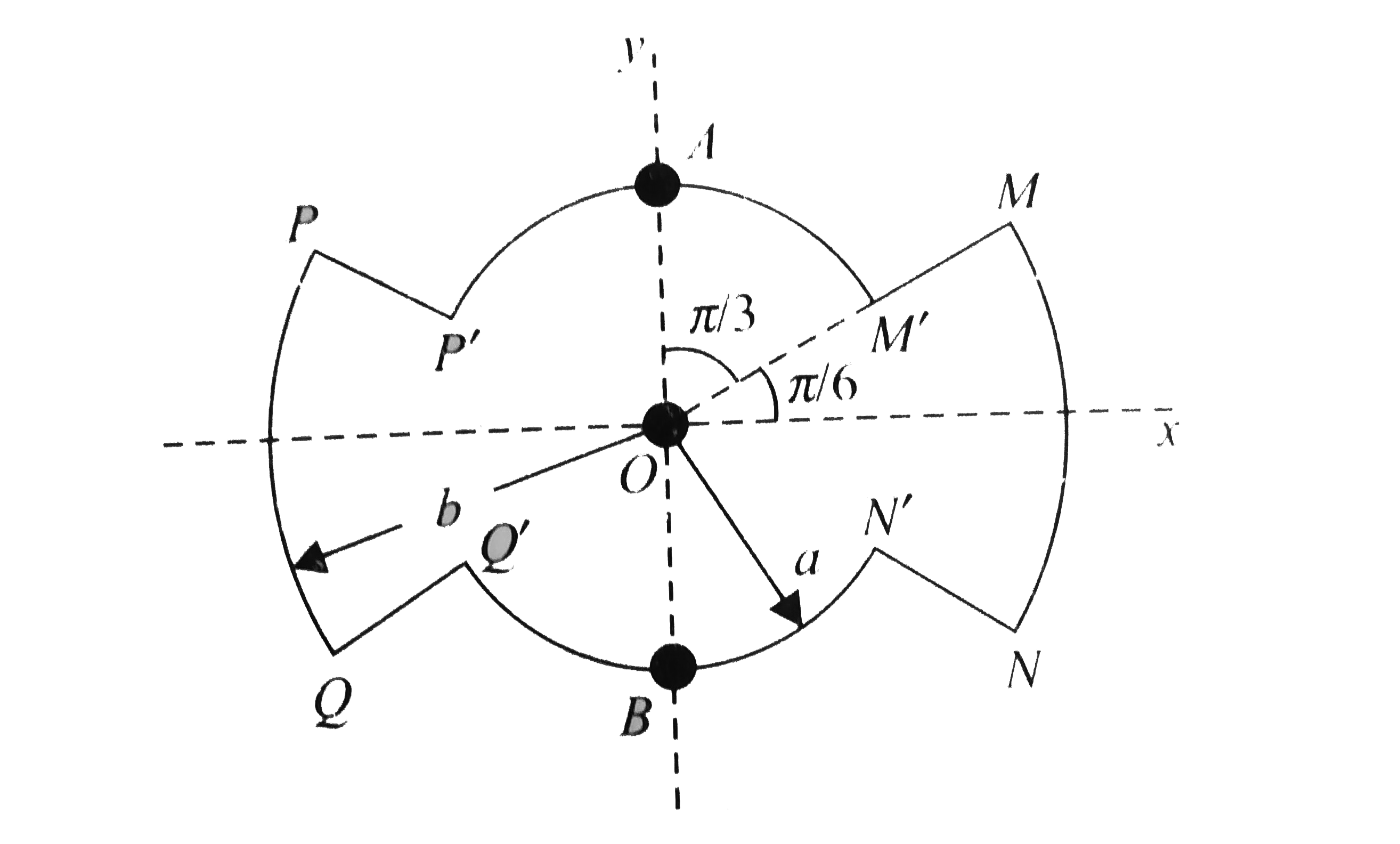
The magnitude of force experienced by the arc MN is
zero
μ0VI0πRb
μ0VI02πRb
none of these
The correct Answer is:A
(a)
Magnetic field produced by the conductor along z-axis will
be parallel to MN. Hence, force on MN is zero.
Current from B to A (through NM or QP):
I=VR/2=2VR
Force due to I0 on N'N and Q'Q will be out of the paper and on
M'M and P'P will be in the paper. This will produce the torque
Torque on M'M (along negative x-axis):
τ=∫ba(μ0I02πrIdr)rsin(π6)=μ0I04πI(b−a)
=μ0I02V4Rπ(b−a)
Total torque =4τ=2μ0I0VπR(b−a) (along negative x-axis.)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (integer)
Explore 7 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Archives (fill In The Blanks)
Explore 1 Video
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
A long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View Solution
Knowledge Check
There exists a long conductor along z-axis carrying a current I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference VBA=V is applied. Radii of arcs are a and b, respectively, as shown in the figure.
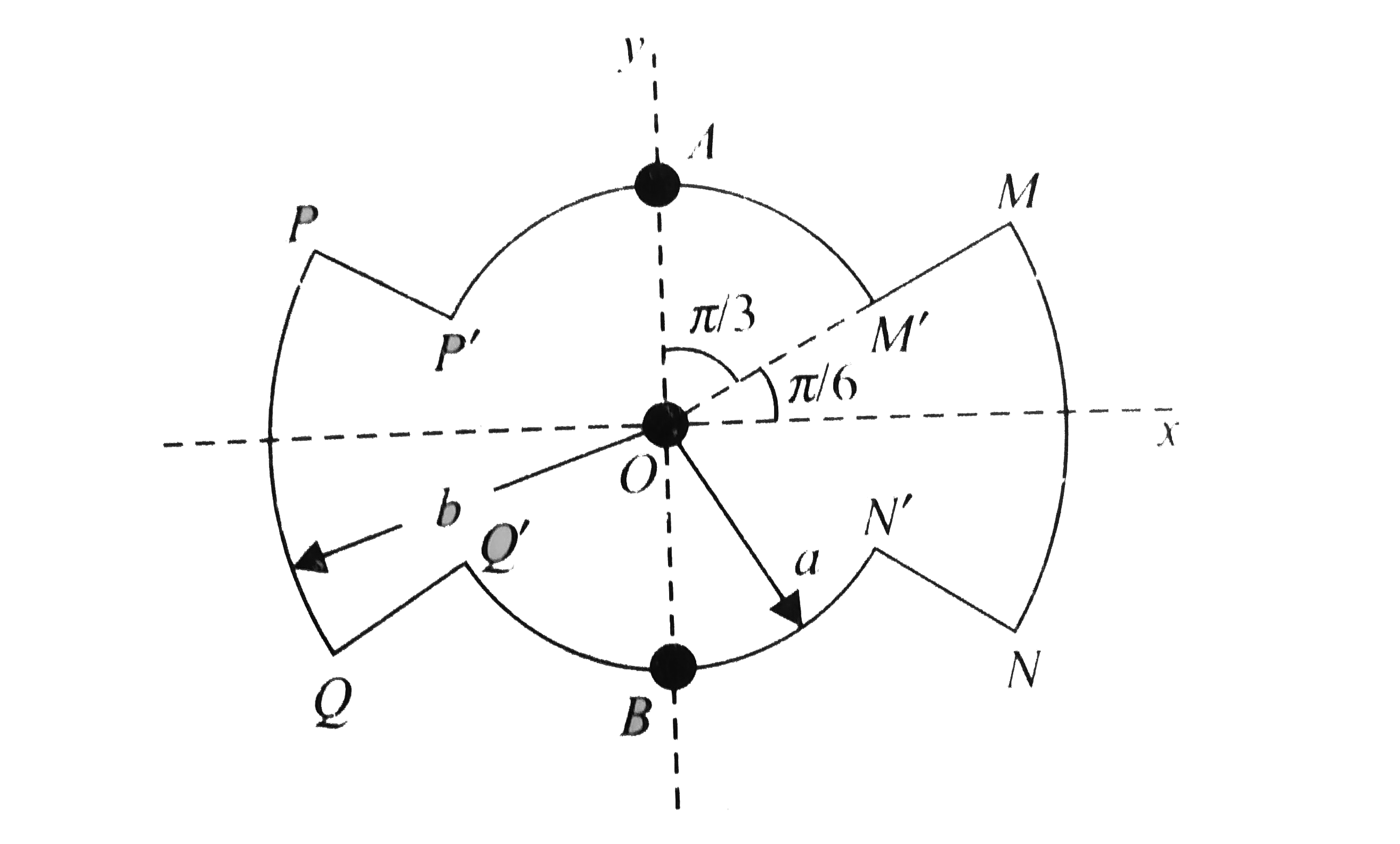
The total torque acting on the loop is nearlyAμ0VI0πR(b−a)ˆiB−2μ0VI0πR(b−a)ˆiCμ0VI02πR(b−a)ˆiDnone of theseA long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+Y2)Bμ0I(xˆi+yˆj)2π(x2+Y2)Cμ0I(xˆj−yˆi)2π(x2+Y2)Dμ0I(xˆi−yˆj)2π(x2+Y2)
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
View SolutionA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
View SolutionAn electron moving with a velocity v along the positive x-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is
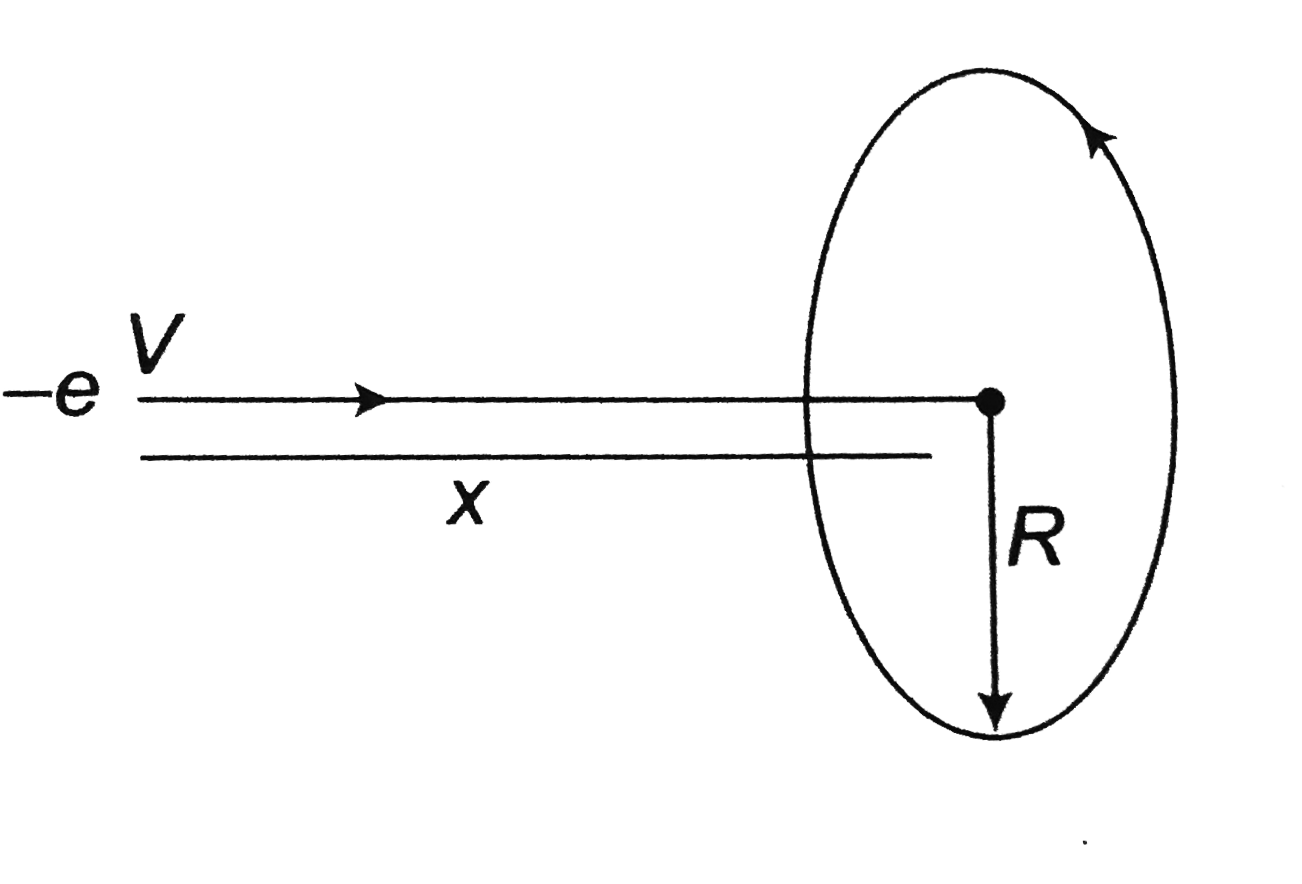
View SolutionA long straight wire is kept along x-axis. It carries a current i in the positive x-direction. A proton and an electron are placed at (0, a,0) and (0, -a, 0) respecitively. The proton is imparted an initial velocity v along +z axis and the electron is imparted an initial velocity v along +x-axis. The magnetic forces experienced by the two particles at the instant are
View SolutionAn electron moving with a velocity v along the positive x-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is

View Solution
