A charge Q is uniformly distributed over a ring which is rotating with constant angular velocity ω about an axis passing through its centre and perpendicular to the plane. A wire which carries a current I is lying perpendicular to the plane of the irng along its axis having one end at its centre. Find resultant magnetic force on the wire by the ring.
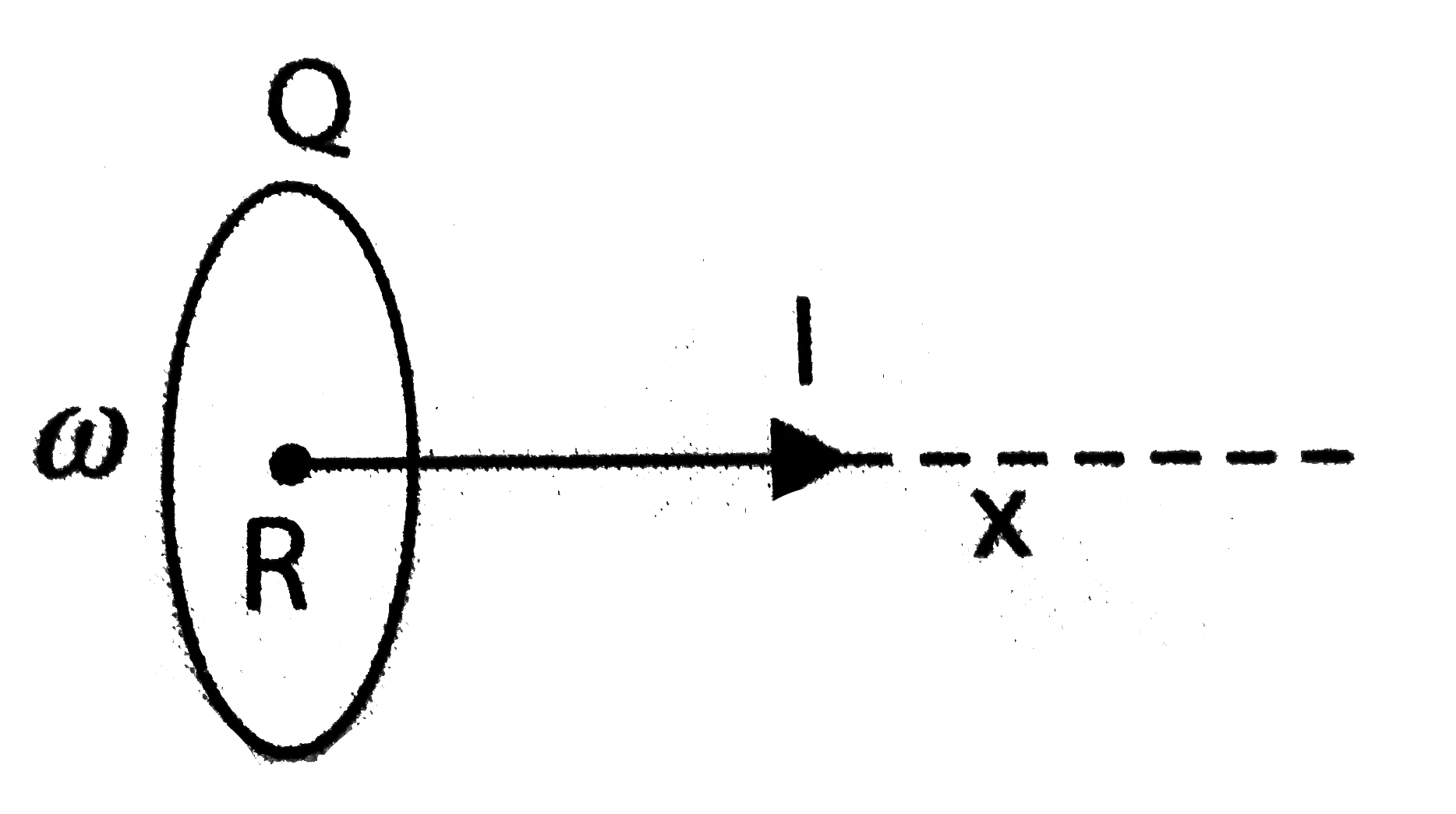
Magnetic field due to ring will be parallel to wire, hence force
on the wire will be zero.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (single Correct )
75 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View Solution
Knowledge Check
Moment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
AI=12MR2BI=MR2CI=32MR2DI=52MR2The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR/√2BR/2C√2 RD2R
A charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View Solutiona semicircle wire of radius R is rotated with constant angular velocity about an axis passing through one end and perpendicular to the plane of wire. There is a uniform magnetic field of strength B. The induced emf between the ends is

View Solution
