Consider a hypothetic spherical body. The body is cut into two parts about the diameter. One of hemispherical portion has mass distribution m while the other portion has indentical charge distribution q. The body is rotated about the axis with constant speed Then, the ratio of magnetic moment to angular momentum is
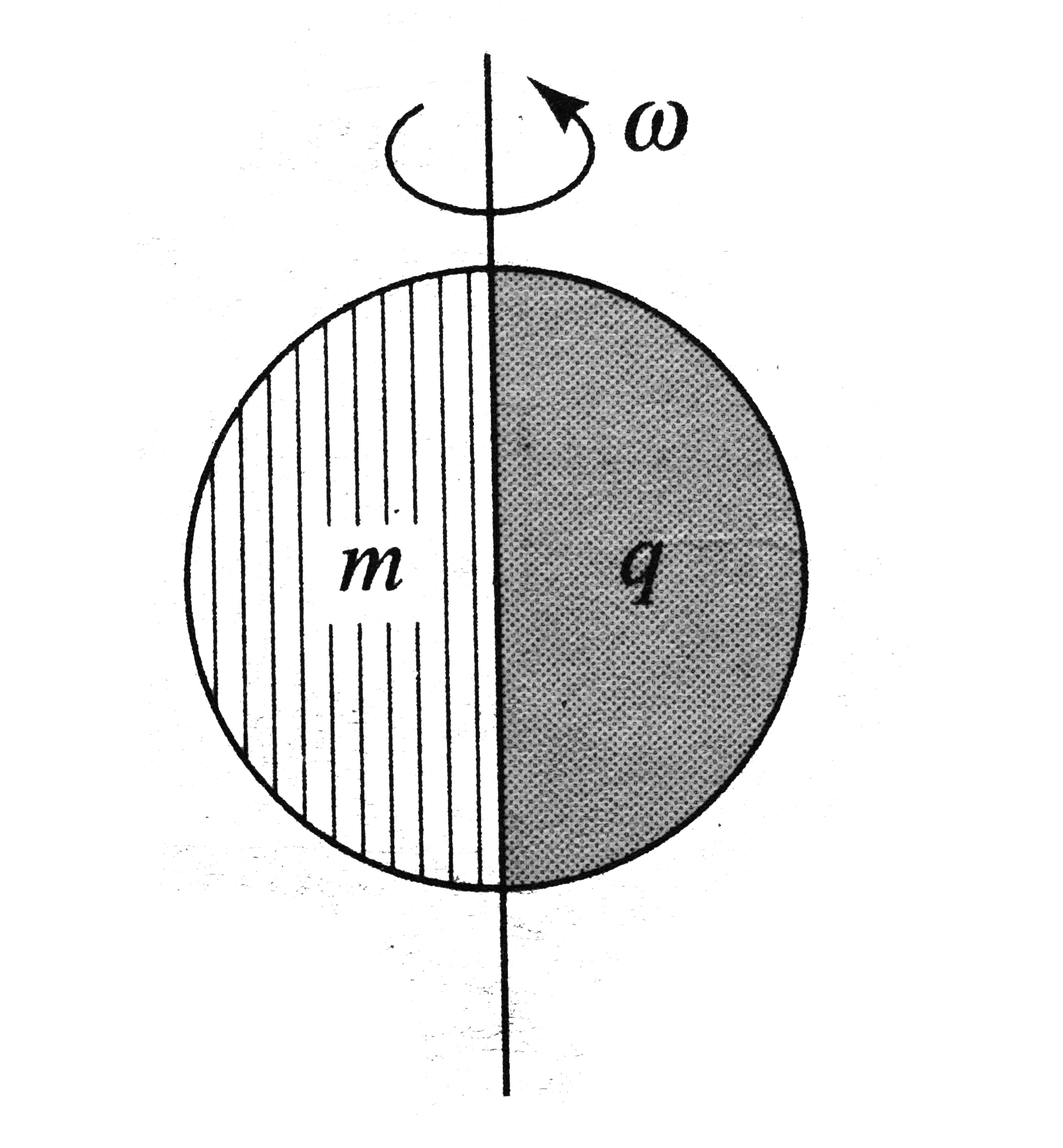
cannot be calculated
The correct Answer is:a
The ration is always .
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A thin uniformring of radius R carrying uniform charge Q and mass M rotates about its axis with angular velocity ω. The ratio of its magnetic moment and angular momentum is:
View SolutionA charge q is given to a solid conducting sphere of mass m and is rotating about it's diameter with angular velocity omega .Then ratio of it's magnetic moment to its angular momentum is ..
View Solution
Knowledge Check
A thin disc of radius R and mass M has charge q uniformly distributed on it. It rotates with angular velocity ω. The ratio of magnetic moment and angular momentum for the disc is
Aq2MBR2MCq22MD2MqA rod of length l having uniformly distributed charge Q is rotated about one end with constant frequency f Its magnetic moment
AπfQl2BπfQl23C2πfQl23D2πRQ2A thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
AQR2ω8BQR2ω4CQR2ω2DZero
If two charged particles each of charge q mass m are connected to the ends of a rigid massless rod and is rotated about an axid passing through the centre and ⊥ to length. Then find the ratio of magnetic moment to angular momentum.
View SolutionConsider a non conducting plate of radius a and mass m which has a charge q distributed uniformly over it, The plate is rotated about its own axis with a angular speed ω. Show that the magnetic moment M and the angular momentum L of the plate are related as ML=q2m.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionConsider a solid sphere of radius r and mass m which has a charge q distributed uniformly over its volume. The sphere is rotated about a diameter with an angular speed ω. The magnetic moment of the sphere is
View SolutionThe diameter of a disc is 1m. It has a mass of 20kg. It is rotating about its axis with a speed of 120 rotations in one minute. Its angular momentum in kgm2/s is
View Solution
