A particle of charge per unit mass α is released from origin with velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(>π3B0α) would be
√32v0B0α+√32v0(t−πB0α)
√32v0B0α+v0(t−π3B0α)
√32v0B0α+v02(t−π3B0α)
√32v0B0α+v0t2
The correct Answer is:c
r=mv0B0q=v0B0α,xr=√32=sinθ
⇒θ=60∘
tOA=T6=π3B0α
Therefore, x-coordinate of particle at
any time t>π3B0α will be
x=√32v0B0α+v0(t−π3B0α)cos60∘
=√32v0B0α+v02(t−π3B0α)
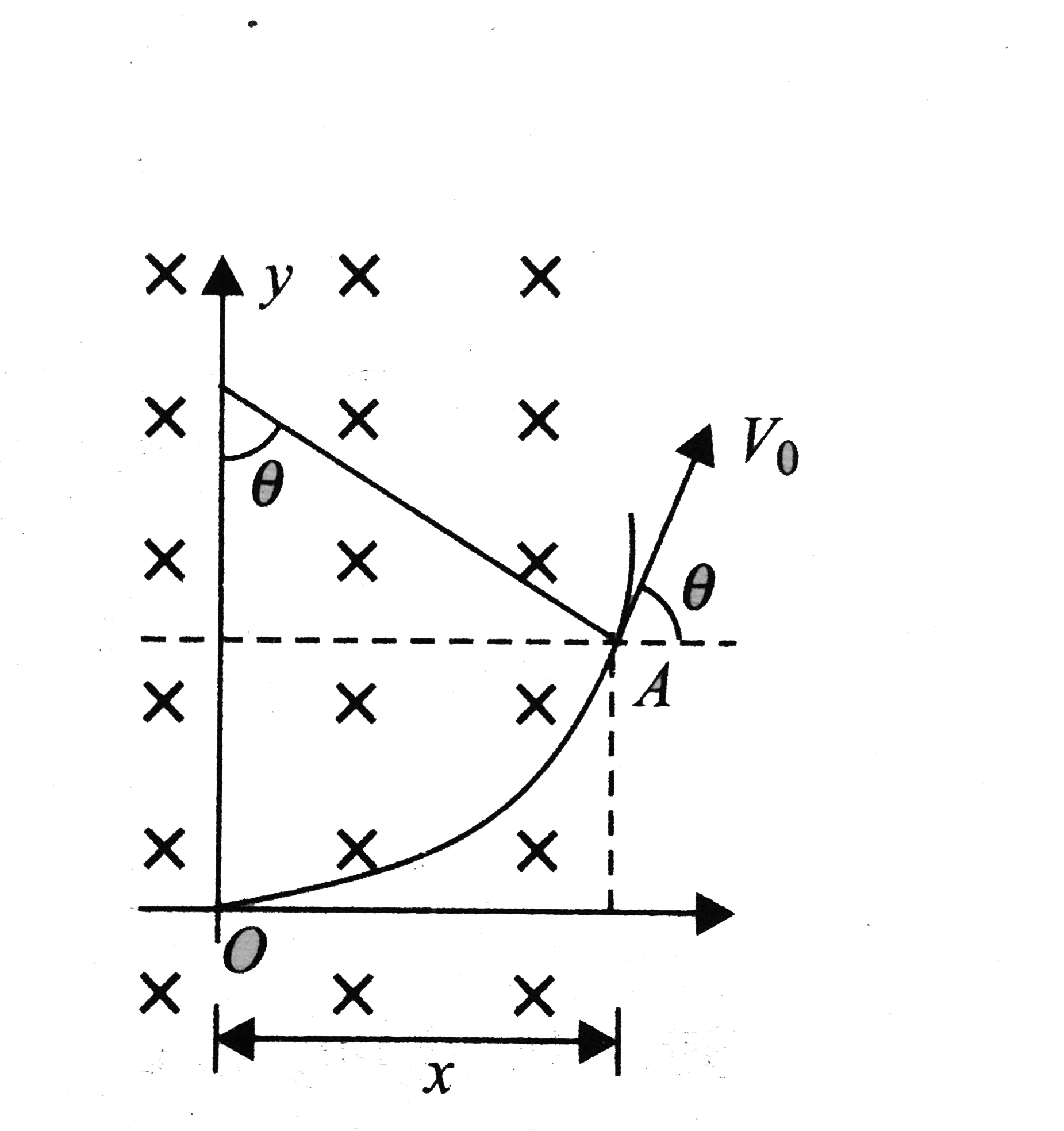
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Subjective
10 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View Solution
Knowledge Check
The x -co- ordinates of the particle at time t (>π3B0α) would be
A−2V0B0αB−V0B0αC2V0B0αD−V0B0αA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would beA√32v0B0α+√32v0(t−πB0α)B√32v0B0α+v0(t−π3B0α)C√32v0B0α+v02(t−π3B0α)D√32v0B0α+v0t2A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi uniform magnetic field →B=−B0ˆk. If the particle passes through (0,y,0), then y is equal to
A−2v0B0αBv0B0αC2v0B0αD−v0B0α
A particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionA charged particle of specific charge (charge/mass) α released from origin at time t=0 with velocity →v=v0(ˆi+ˆj) in uniform magnetic field →B=B0ˆi. Coordinates of the particle at time t=π/(B0α) are
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View Solution
