A particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
Magnetic field is along negative z-direction. So in the coordinate axes sonw in figure, it is perpendicular to paper inwards. Mgnetic force on the particle at origin is along positive y-directio. So, it will rotat in xy-plane as shown. The path is not a perfect circle as the magnetic field is non uniform. Speed of the particle in magnetic field remains constant. Magnetic force is always perpendiculr to velocity. Let at point P(x,y) its velocity vector makes an angle theta with positive x-axis. The magnetic force Fm will be angle θ with positive y-direction.So,
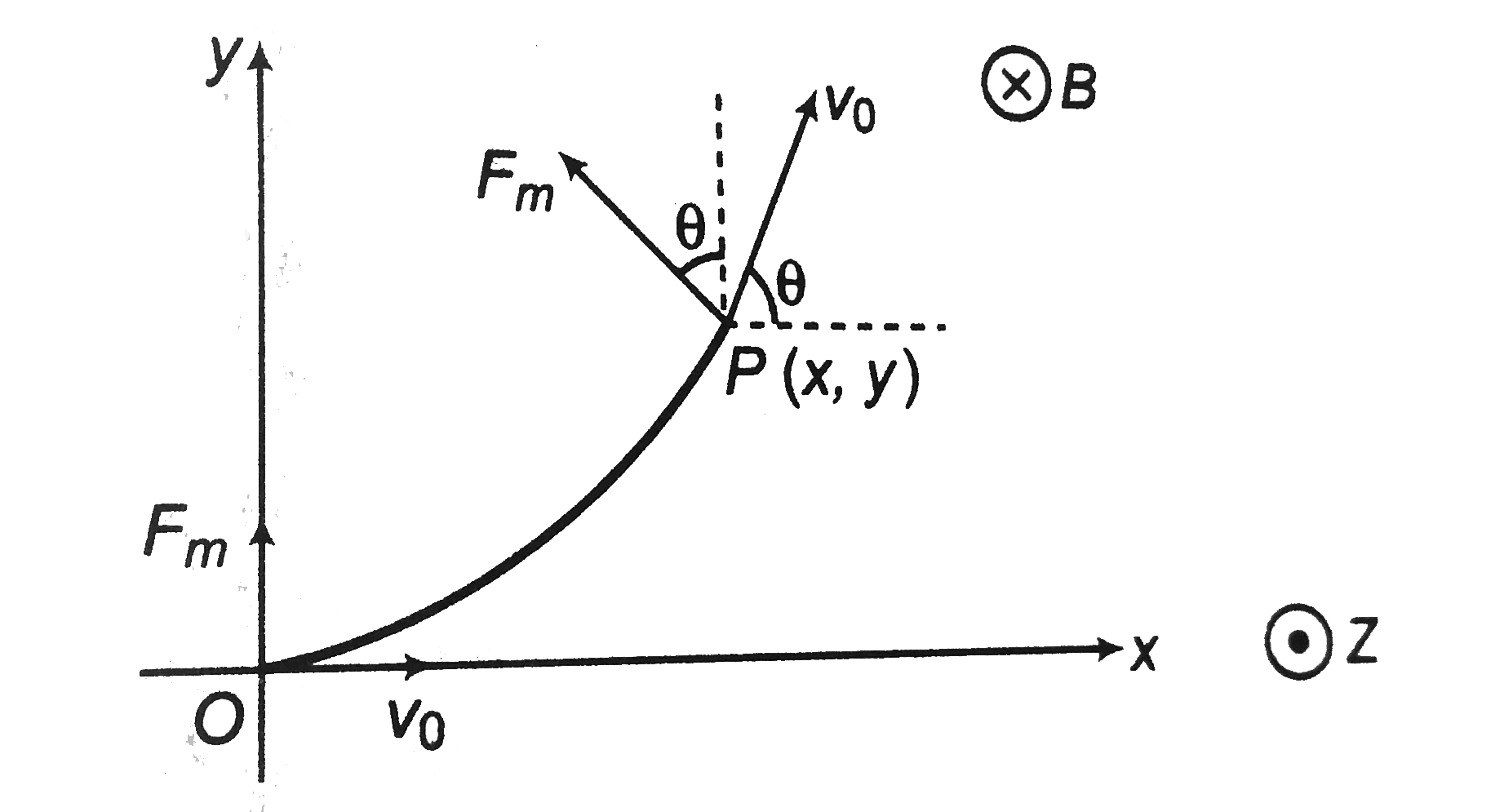
ay=(Fmm)cosθ
∴dvydt=((B0x)(qv□)cosθ)0m[Fm=Bqv0sin90∘]
∴(dvydx).(dxdt)=B0qxm(v0cosθ)
Here,dxdt=vx=v0cosθ
∴dvydx=(B0qm)x
∴∫v00dvy=(B0qm)∫xmax0xdx
∴v0=(B0qm)x2max2
∴xmax=√mv02B0q
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - Exercise
160 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A particle of mass m and charge + q is projected from origin with velocity →V=V0ˆi in a magnetic field →B=−(B0x)ˆk. Here V0 and B0 are positive constants of proper dimensions. Find the radius of curvature of the path of the particle when it reaches maximum positive x co-ordinate.
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View Solution
Knowledge Check
A particle of charge 'q' and mass 'm' is projected from the origin with velocity (u0ˆi+v0ˆj) in a gravity free region where uniform electric field −E0ˆi and uniform magnetic field −B0ˆi exist. Find the condition so that the particle would return to origin at least for once .
Aμ0B02πE0 is an integerB√u20+v20B0πE0 is an integerCv0B0πB0 is an integerDμ0B0πE0 is an integerA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Maximum z-coordinate of the particle isA√3mv0B0qB2√3mv0B0qC2mv0B0qDmv0B0qA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
When z-co-ordinate has its maximum valueAvx=0Bvy=v0CBoth (a) and (b) are correctDBoth (a) and (b) are wrong
A particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionA particle of charge q and mass m released from origin with velocity →v=v0ˆi into a region of uniform electric and magnetic fields parallel to y-axis. i.e., →E=E0ˆjand→B=B0ˆj. Find out the position of the particle as a functions of time
Strategy : Here →E∣∣→B
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
ay=Fym=Fem=qE0m
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
→v(t)=vxˆi+vyˆj+vzˆk
View SolutionA particle of charge per unit mass α is released from origin with velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(>π3B0α) would be
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View Solution
