A radioactive substance X decays into another radioactive substance Y. Initially, only X was present . λx and λy are the disintegration constant of X and Y. Ny will be maximum when.
NyNx−Ny=λyλx−λy
NyNx−Ny=λyλx−λy
λyNy=λxNx
λyNx=λxNy
The correct Answer is:C

NetrateforamtionofYatanytimetis<br>(dN_(y))/(dt) =lamb_(y) N_(y)daxNx−λ
Ny is maximum when
dNydt=0
or λxNx−λyNy.
Topper's Solved these Questions
- NUCLEAR PHYSICSBook:CENGAGE PHYSICSChapter:NUCLEAR PHYSICSExercise:Linked Comprehension
Explore 29 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICSChapter:NUCLEAR PHYSICSExercise:Integer
Explore 6 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICSChapter:NUCLEAR PHYSICSExercise:Subjective
Explore 35 Videos
- Moving charges and magnetismBook:CENGAGE PHYSICSChapter:Moving charges and magnetismExercise:Question Bank
Explore 20 Videos
- NUCLEIBook:CENGAGE PHYSICSChapter:NUCLEIExercise:QUESTION BANK
Explore 59 Videos
Similar Questions
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionThe half-life period of a radioactive element x is same as the mean life time of another radioactive element y. Initially, both of them have the same number of atoms. Then,
(a) x and y have the same decay rate initially
(b) x and y decay at the same rate always
(c) y will decay at a faster rate than x
(d) x will decay at a faster rate than y
View Solution
Knowledge Check
A radioactive substance X decays into another radioactive substance Y. Initially, only X was present . λx and λy are the disintegration constant of X and Y. Ny will be maximum when.
ANyNx−Ny=λyλx−λyBNyNx−Ny=λyλx−λyCλyNy=λxNxDλyNx=λxNyThe decay constants of a radioactive substance for a and b emission are λa and λb respectively. If the substance emits α and β simultaneously, the average half life of the material will be -
Aλα−λβBλα+λβCλαλβλα+λβDNone of theseA radioactive elementX converts into another stable element Y. Half-life of X is 2h. Initially, only X is present. After time t, the ratio of atoms of X and Y is found to be 1:4 Then t in hours is .
A2B4Cbetween 4 and 6D6
A radioactive isotope X decays simultaneously by two ways α and β decay. The decay constants of α and β decays are λ1 and λ2 and the products formed are Y and Z respectivley. Both Y and Z are stable. Initially. there was no presence of Y and Z in the sample. The process of α decay stops fater time t0. Find the ratio of mass of Y to mass of Z in the sample at time 2t0 the molar masses of Y and Z are My and Mz respectively.
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.

The net rate of accumulation of B at any instant is
View SolutionThe half - life (T) and the disintegration constant (λ) of the radioactive substance are related as
View SolutionTwo samples X and Y contain equal amounts of radioactive substances. If 116th of a sample X and 1256th of sample Y remain after 8h, then the ratio of half periods of X and Y is
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
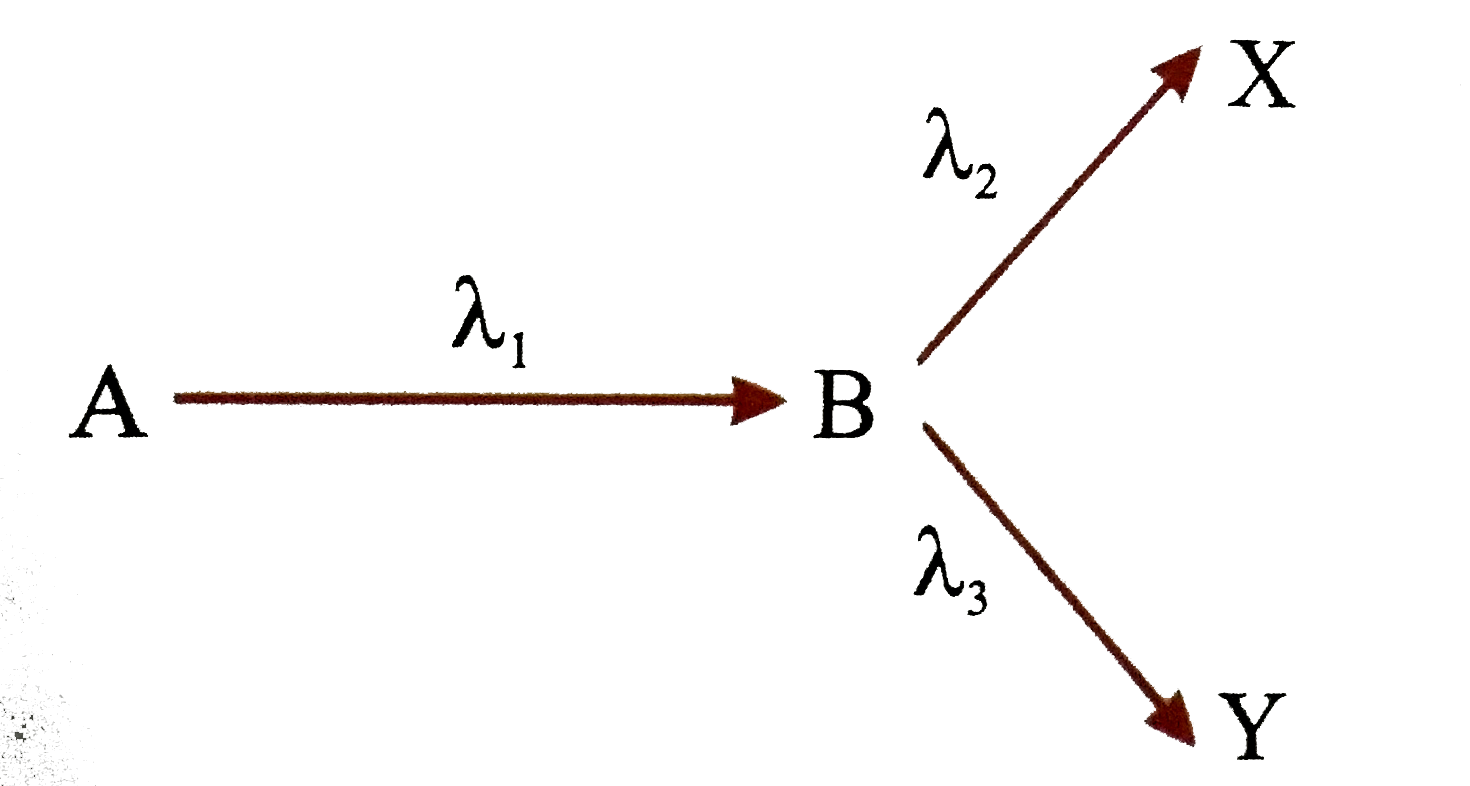
At t=∞, which of following is incorrect ?
View Solution