In problem43, number of atoms decayed between time interval t1 and t2 are
ln(2)λ(R1R2)
R1e−λt2−R2e−λt2
λ(R1−R2)
R1−R2λ)
The correct Answer is:d
R1=λN1⇒N1=R1λ
and R2=λN2⇒N2=R2λ
Therefore, number of atoms decayed =N1−N2=(R1−R2λ).
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - NUCLEAR PHYSICSEXERCISE - Linked Comprehension
29 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - NUCLEAR PHYSICSEXERCISE - Integer
6 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - NUCLEAR PHYSICSEXERCISE - Subjective
35 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
- NUCLEIBOOK - CENGAGE PHYSICSCHAPTER - NUCLEIEXERCISE - QUESTION BANK
59 Videos
Similar Questions
A radioactive substance has a half-life of 64.8 h. A sample containing this isotope has an initial activity (t=0) of 40μCi. Calculate the number of nuclei that decay in the time interval between t1=10.0h and t2=12.0h.
View SolutionA point moving in a straight line with uniform acceleration describes aand b feet in successive intervals of t1 and t2 seconds. Then the acceleration is 2(bt1−at2)t1t2(t1+t2)
Also if the point describes equal distances in successive times t1,t2,t3 then
1t1−1t2+1t3=3t1+t2+t3
View Solution
Knowledge Check
The half life of a radioactive substance is 20 days. If 23 part of the substance has decayed in time t2 and 13 part of it has decayed in time t1 then the time interval between t2 and t1 is (t2−t1)=…………….
A5 daysB10 daysC20 daysD40 daysThe radioactivity of a sample is A1 at time t1 and A2 at time t2 If the mean life of the specimen is T, the number of atoms that have disintegrated in the time interval of (t2−t1) is :
A(A1−A2)B(A1−A2)TC(A1−A2)TDA1t1−A2t2Two first order freaction have half-lives in the ratio 8:1 Calculate the ratio of time intervals t1:t2 and t1 and t2 are the time period for (14)th and (34)th completion.
A1:0.301B0.125:0.602C1:0.602Dnone of these
Find average speed in time interval t= 2 to t=10s
View SolutionA body moving in a straight line with uniform acceleration describes three successive equal distances in time intervals t1,t2andt3 respectively. Show that
1t1−1t2+1t3=3t1+t2+t3
View SolutionState the law of radioactive decay.
Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half-life T12.
Depict in the plot the number of undecayed nuclei at (i) t=T12 and (ii) t=5T12.
View SolutionA particle is projected with speed u at angle θ with horizontal from ground . If it is at same height from ground at time t1andt2 , then its average velocity in time interval t1 to t2 is
View SolutionAssertion : In the υ−t diagram as shown in figure, average velocity between the interval t = 0 and t=t0 is independent of t0
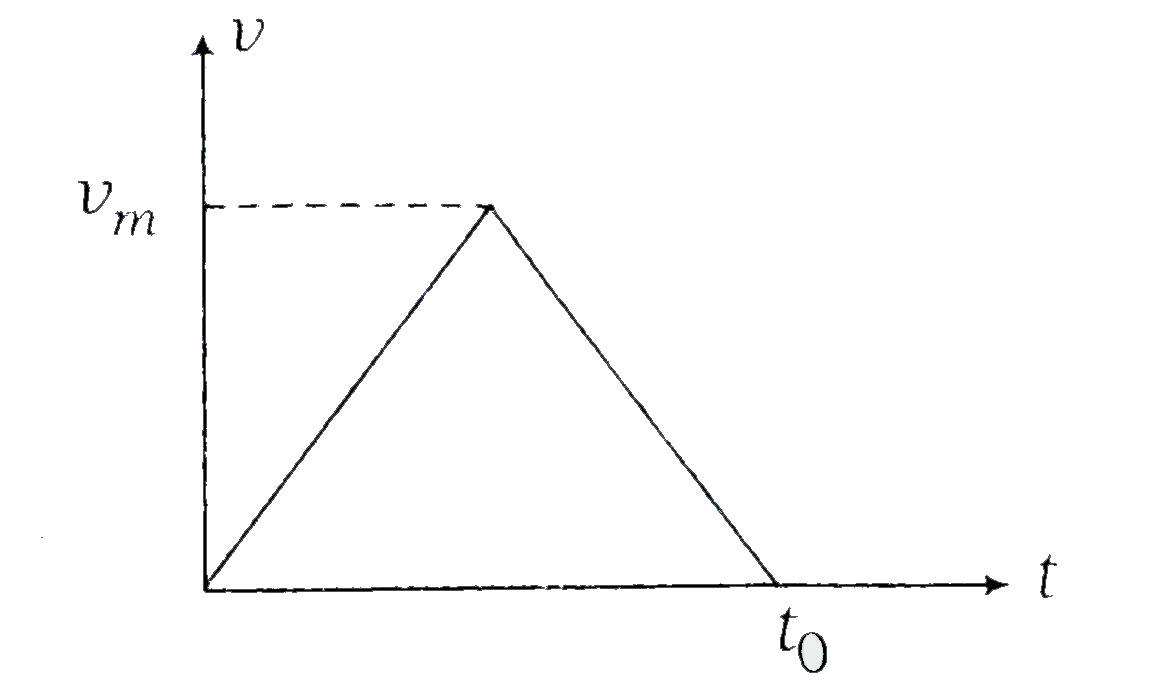
Reason : Average velocity in the given interval is 12υm.
View Solution
