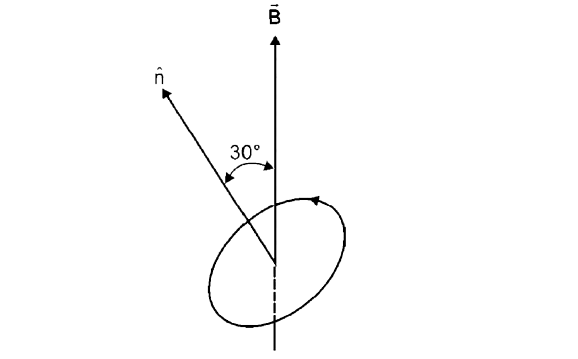
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
a. If f is the frequncy of orbital motion then the orbital magnetic dipole moment of circulating electron.
M=IA=feA
According to Bohr's condition of stationary orbits
mvR=nh2π
For ground state, n=1andareaA=πR2
Also, v=Rω=R2πf
∴m(R2πf)R=1h2π
∴f=h4π2mR2
∴FromEq(i),M=(h4π2mR2)eπR2
⇒M=eh4πmA−m2
b.The direction of magnetic moment is along normal to the plane of electron orbit , i.e., alone ˆn
τ=MB sin theta =(eh4πm)Bsin30∘
i.e.τ=ehB8πm newton xx meter
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.115videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.212videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - QUESTION BANK65videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK40videos
ATOMS
Similar Questions
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

Obtain an expression for the orbital magnetic dipole moment of the electron.View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
View SolutionMagnetic dipole moment of revolving electron is
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
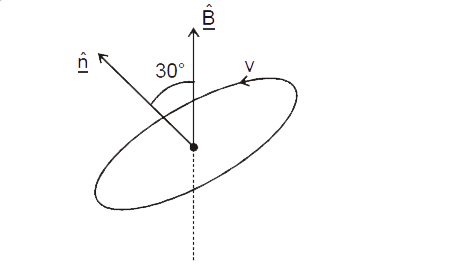
The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.View SolutionThe minimum magnetic dipole moment of electron in hydrogen atom is
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clock wise direction in a circular orbit. The atom is placed in a magnetic filed such that the normal to the electron orbit makes an angle of 30° with the magnetic field. Find the torque experienced by the orbiting electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.View SolutionShow that the orbital magnetic dipole moment of a revolving electron isevr/2.
View Solution


