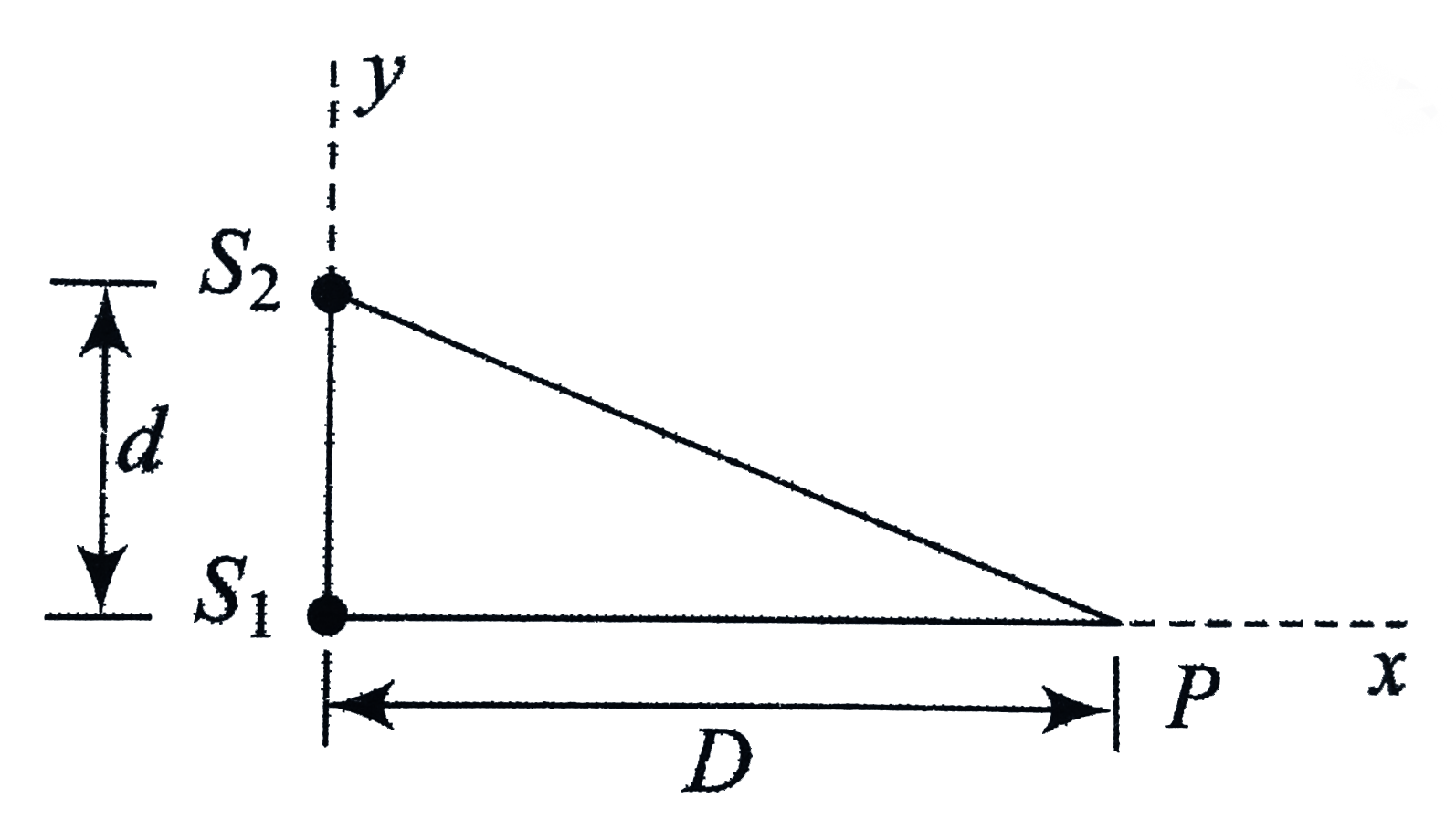
Two sources S1 and S2 emitting light of wavelength 600 nm placed a distance 1.0×10−2 cm apart.
A detector can be moved on line S1P which is perpendicular to S1S2
(a) What would be the minimum and maximum path difference at the detector as it moves along line S1P ?
(b) Locate the position of the farthest minima detected
 .
.
a. Path difference at P,Δx=S2P−S1P
Minimum path difference will occur when the observer will be at a large distance from the sources. The Path difference will be maximum when the observer is near source S1. As observer moves from S1 toward +x− direction, the path difference decreases from d to zero.
(Δx)max : when S1P, i.e., detector is at positionS1.
∴(Δx)max=S1S2=d=1.0×10−2m
(Δx)min : when detector is at large distance and
(Δx)min will be apprximately zero.
b. Let the farthest minimum occur at P. As we move away increases as we move toward S2. At the position of the farthest minimum path difference is
S2P−S1P=λ/2
(D2+d2)1/2−D=λ/2
[D(1+d2D2)1/2]−D=λ/2
d22D=λ2⇒D=d2λD=d2λ=λ4=1.7cm
 .
.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Solved Examples
10 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
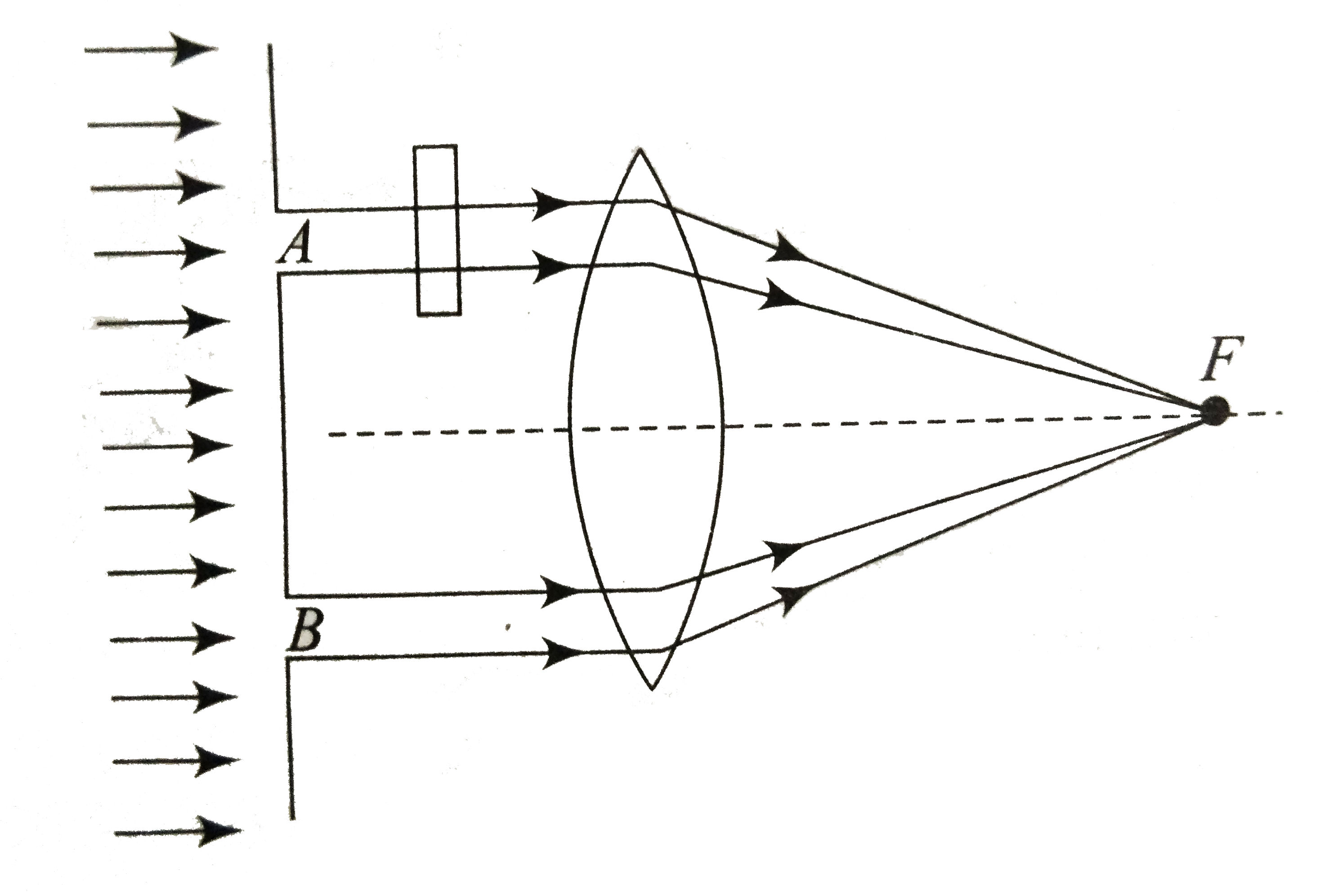
In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
View SolutionTwo coherent sources of light of intensity ratio β produce interference pattern. Prove that in the interferencepattern
Imax−IminImax+(Imin)=2√β1+β
where Imax and Imin are maximum and mininum intensities in the resultant wave.
View SolutionThe figure shows two paths through which a gas can be taken from state A to state B. If the ratio of work done by the gas in the two paths is xy, then find (x+y).
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionA string of length 1m fixed at both ends is vibrating in 3rd overtone. Tension in string is 200N and linear mass density is 5 gmin. Frequency of these vibrations is (in Hz ).
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda . The separation between the sources is 2lambda . Consider a line passing through S_(1) and perpendicular to line S_(1) S_(2) . Find the position of farthest and nearest minima. .
View SolutionTwo source of sound, S_(1) and S_(2) , emitting waves of equal wavelength 2 cm , are placed with a separation of 3 cm between them. A detector can be moved on a line parallel to S_(1) S_(2) and at a distance 24 cm from it. Initially, the detecor is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.
View SolutionTwo coherent sources Sf and S2 (in phase with ech other) are placed at a distance of 2λ as shown where λ is wavelength of sound. A detector moves on line AB parrallel to S1S2. If detector detects maximum intensity at finite distance from O at θ=±(πn). Find n

View Solutionधवनि की दो स्त्रोत S1 एव S2 एक दूसरे से -20.0 cm की दुरी पर रखे हुआ है तथा दोनों ही हवा में 20.0 cm तरंगदैर्ध्य की धवनि तरंगे उत्पान करते है एक सुसूचक को S1S2 रेखा के समांतर तथा उससे 20.0 cm की दुरी पर की रेखा पर खिसकाया जा सकता हिअ प्रारंभ में सुसूचक दोनों स्त्रोत से बराबर दुरी पर है दोनों स्त्रोत से निकलती तरंगो को एक ही कला में मानते हुए बताय की सुसूचक को कितना खिसकाया जय ताकि वह न्यूनतम धवनि सूचित करे
View Solutionदो कला - सम्बन्ध स्त्रोत S1 तथा S2 एक - दूसरे से 1.0×10−2cm की दूरी पर है तथा 600 nm का प्रकाश उत्सर्जित कर रहे है । प्रकाश का एक संसूचक S1S2 पर लंबरेखा S1P पर चलाया जा सकता है
(a) संसूचक को न्यूनतम तथा अधिकतम पंथातर (path difference) कितना मिलेगा ? (b) स्त्रोत से सर्वाधिक दूर न्यूनतम तीव्रता का स्थान पता करे ।
View SolutionTwo microwave sources S_(1) and S_(2) are located at a distance of 4 lambda from each other along Y-axis,with S_(1) at the origin as shown in the figure.A microwave detector D moves along the X-axis away from S_(1) .The first maximum is obtained for x equal to: (wavelength of the microwave is
View SolutionConsider two coherent, monochromatic (wavelength lambda ) sources S_(1) and S_(2) , separated by a distance d. The ratio of intensities of S_(1) and that of S_(2) (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S_(1) is (if the resultant intensity at point P is equal to (9)/(4) times of intensity of S_(1) ) ("Given : "angleS_(2)S_(1)P=90^(@), d gt0 and n" is a positive integer")
View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda .The separation between the sources is 2 lambda .The smallest distance from S_(2) on a line passing through S_(2) and perpendicular to S_(1)S_(2) where a minimum intensity occurs is :
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs ?
View SolutionIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
View SolutionTwo sources S_(1) and S_(2) emiting light of wavelenght 600 nm placed a distance 1.0 xx 10^(-2) cm apart. A detector can be moved on line S_(1) P which is perpendicular to S_(1) S_(2) (a) What would be the minimum and maximum path difference at the detector as it moves along line S_(1) P ? (b) Locate the psoition of the farthest minima detected .
View Solution
