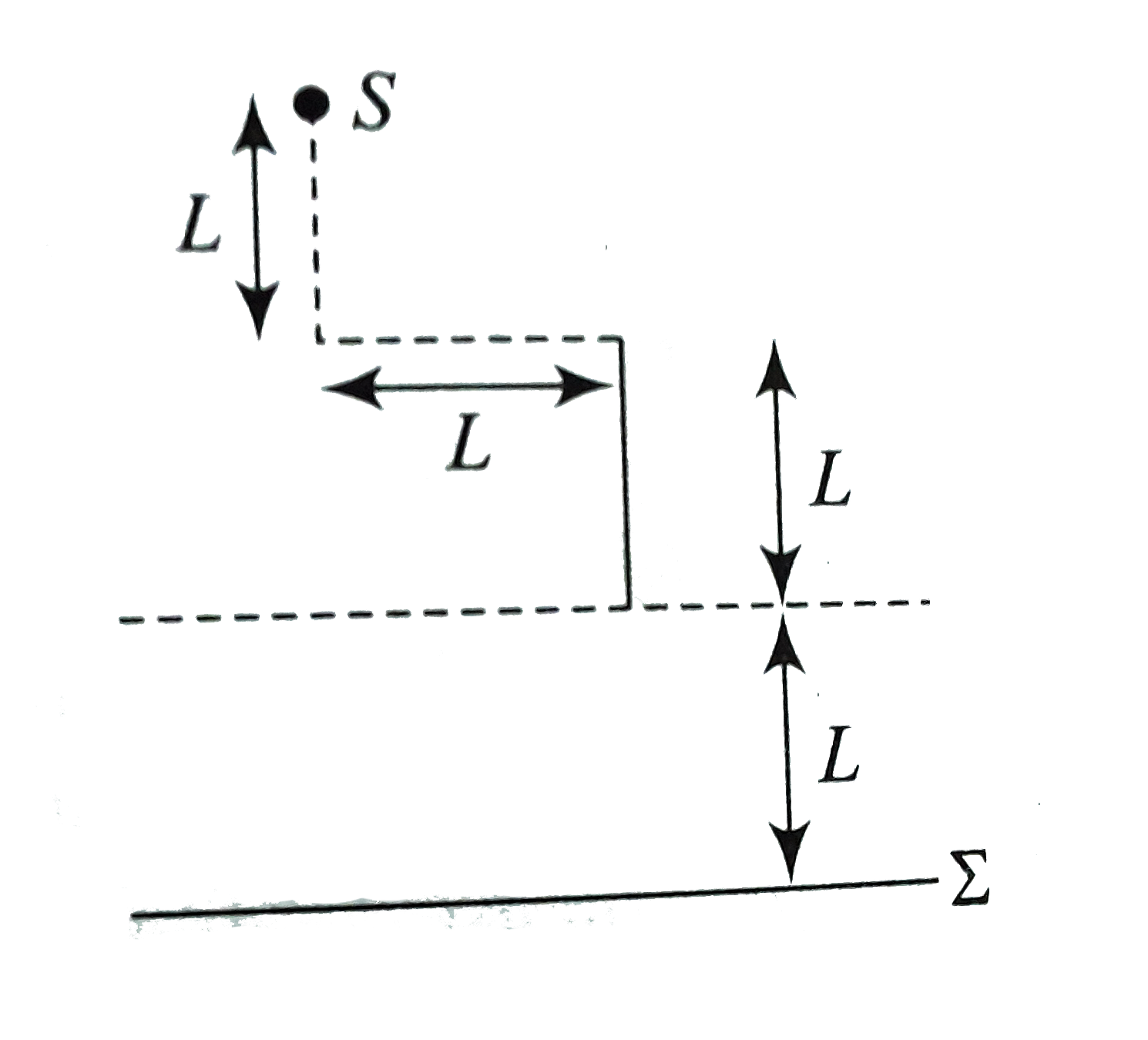
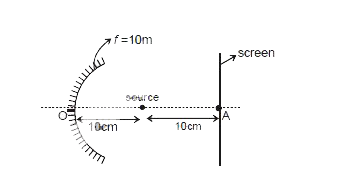A point source of light S is placed in front of a perfectly reflecting mirror as shown in Figure. $Σ$ is a screen. The intensity at the center of screen is found to be I.
If the mirror is removed, then the intensity at the center of screen would be

$I$

$10 I / 9$

$9 I / 10$

$2 I$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c.

Updated on:21/07/2023

A point source of light is placed in front of a plane mirror.
AAll the reflected rays meets at a point when produced backward
Bony the reflected rays close to the normal meet at a point when produced backward
Cony the reflected rays making a smal angle with the mirror meet at point when prodced backward.
Dlight of different colours make different images
A point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen $Σ$

AL
B2L
C $3 L / 2$
D $L / 2$
Light from two coherent sources of the same amplitude A and wavelength $λ$ illuminates the screen. The intensity of the central maximum is $I_{0}$ . If the sources were incoherent, the intensity at the same point will be
A $4 I_{0}$
B $2 I_{0}$
C $I_{0}$
D $\frac{I_{0}}{2}$