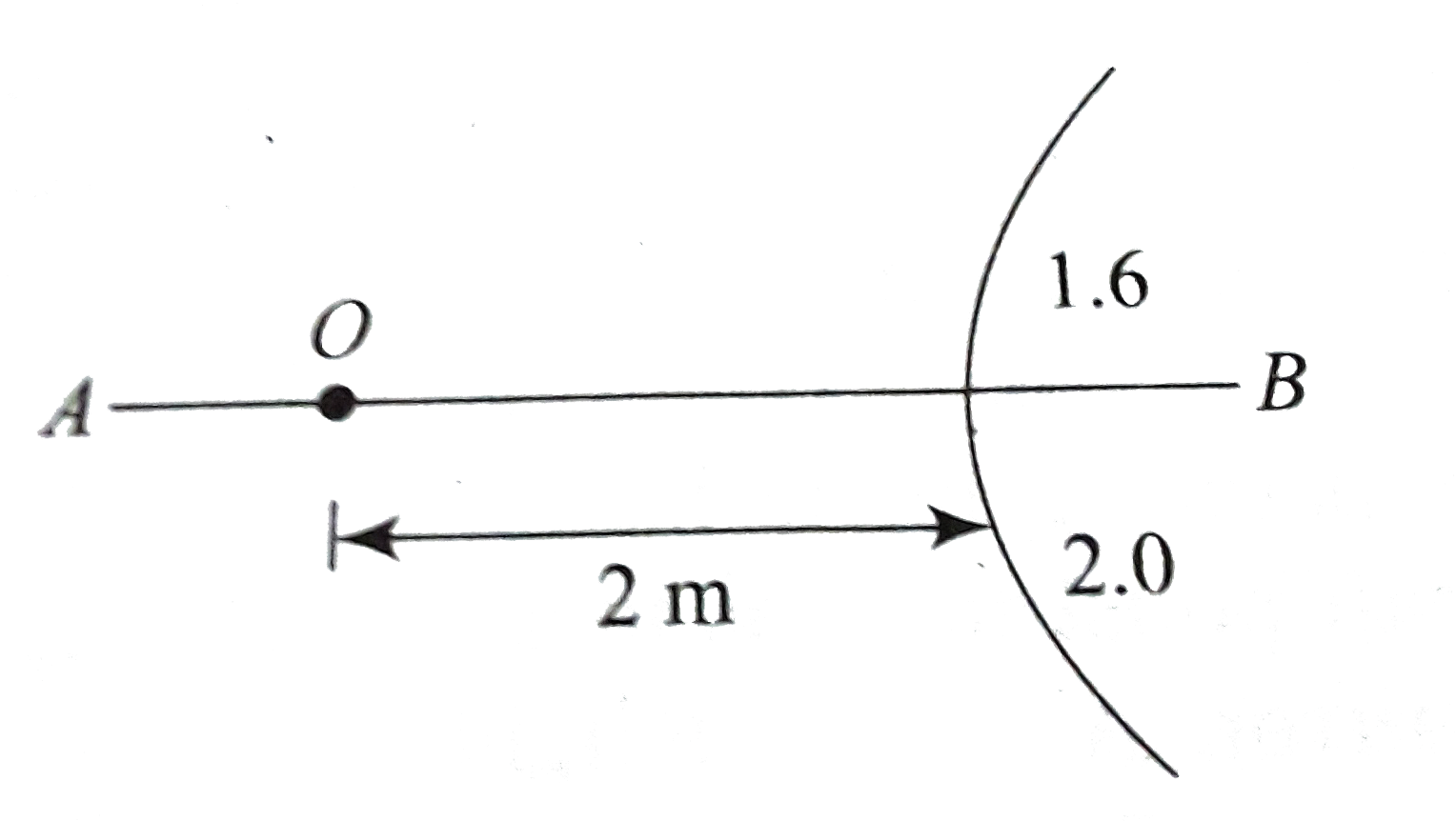
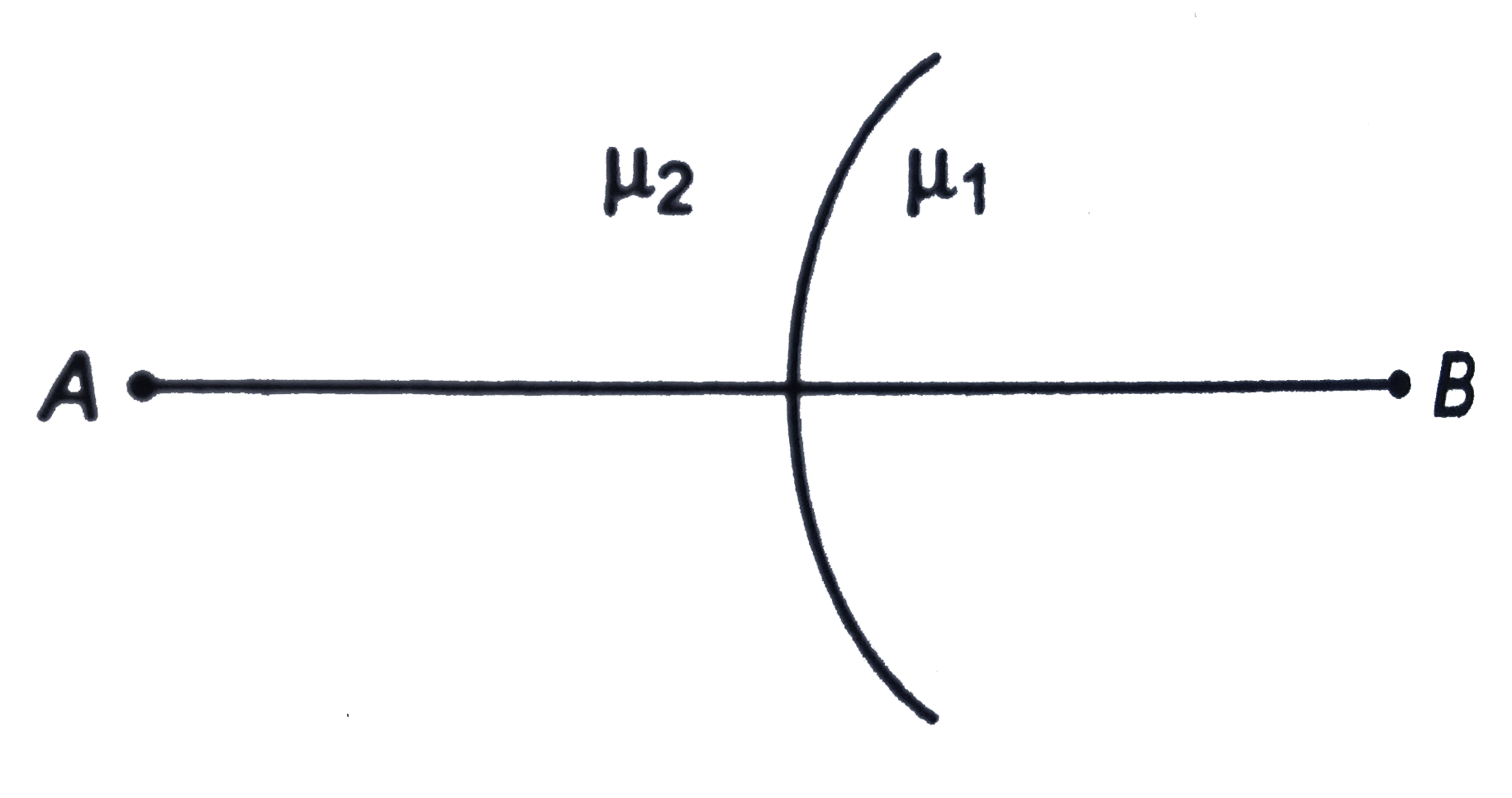
In Figure, a point object O is placed in air. A spherical boundary separates two media. Ab is the principall axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at a the spherical surface is (assume the radius of curvature (R) to be 1 unit)
12m
20m
14m
10m
The correct Answer is:a.
Use refraction formulae separately, that is for air and μ=1.6, and for air and μ=2.0 and positions of the two images.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Assertion-Reasoninig
Explore 2 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Linked Comprehension
Explore 51 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Subjective
Explore 26 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
In the figure shown, a point object O is plaiced in air. A spherical boundary of radius of curvature 1.0(~m) separates various media. AB is the principal axis. The retive index above AB is 1.6 and below AB is 2.0. The separation(in m ) between the images formed due to retion at spherical surface is
'(##CEN_KSR_PHY_JEE_C26_E01_033_Q15##)'
View Solution(a) A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices nx and n2(n2>n1)
Draw the ray diagram and deduce the relation between the object distance (w), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
(b) A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
View Solution
Knowledge Check
In the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is
 A12mB20mC14mD10m
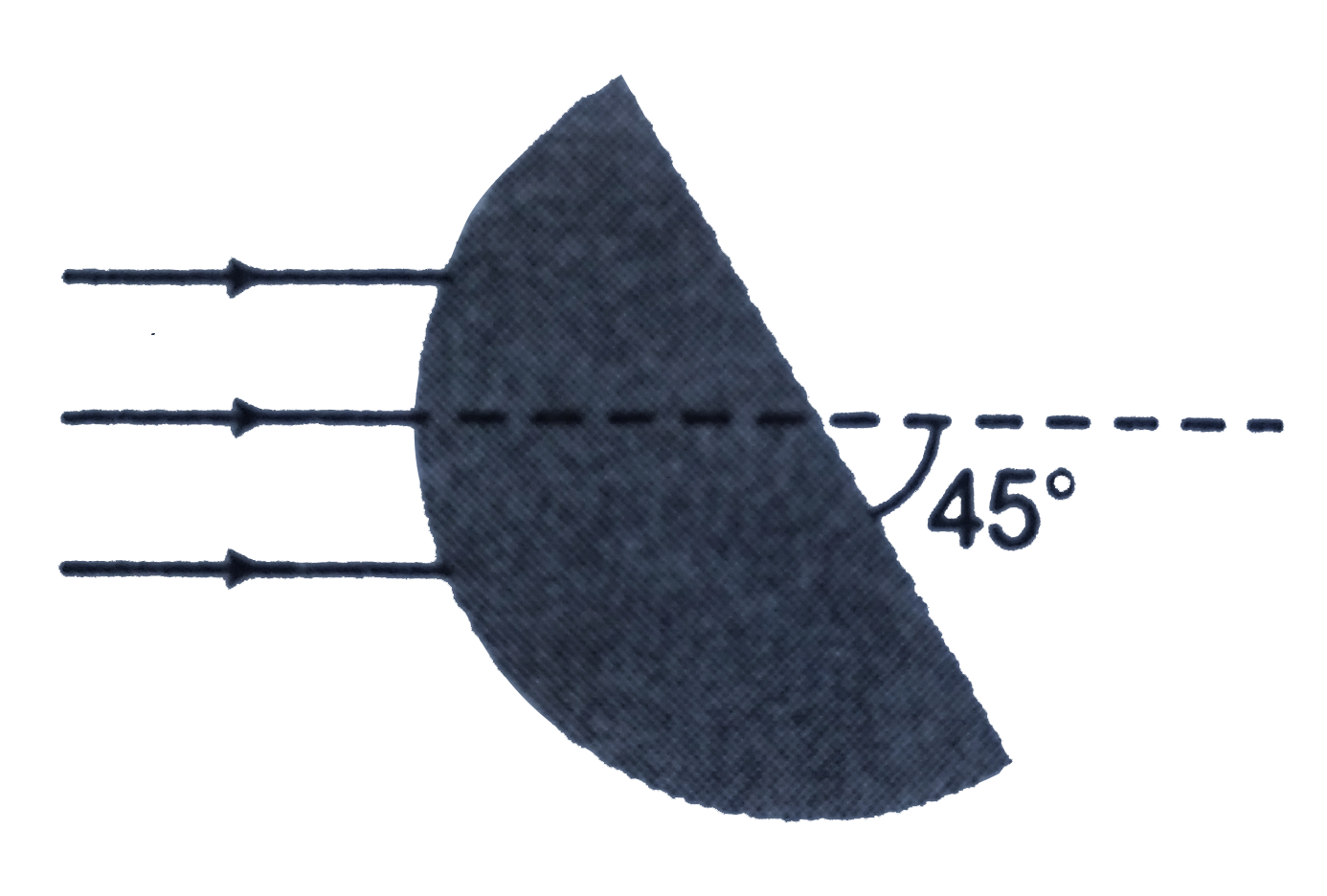
A12mB20mC14mD10mA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
 AR2B3RCR3D2R
AR2B3RCR3D2RA point object is placed in air at a distance of 40 cm from a concave refracting surface of refractive index 1.5. If the radius of curvature of the surface is 20 cm, then the position of the image is –
Ain air and at 30 cm from poleBin refracting medium and at 30 cm from poleCin air and at infinityDin refracting medium and at infinity
In Fig, find position of second image I2 formed after two times refraction from two place surfaces AB and CD.
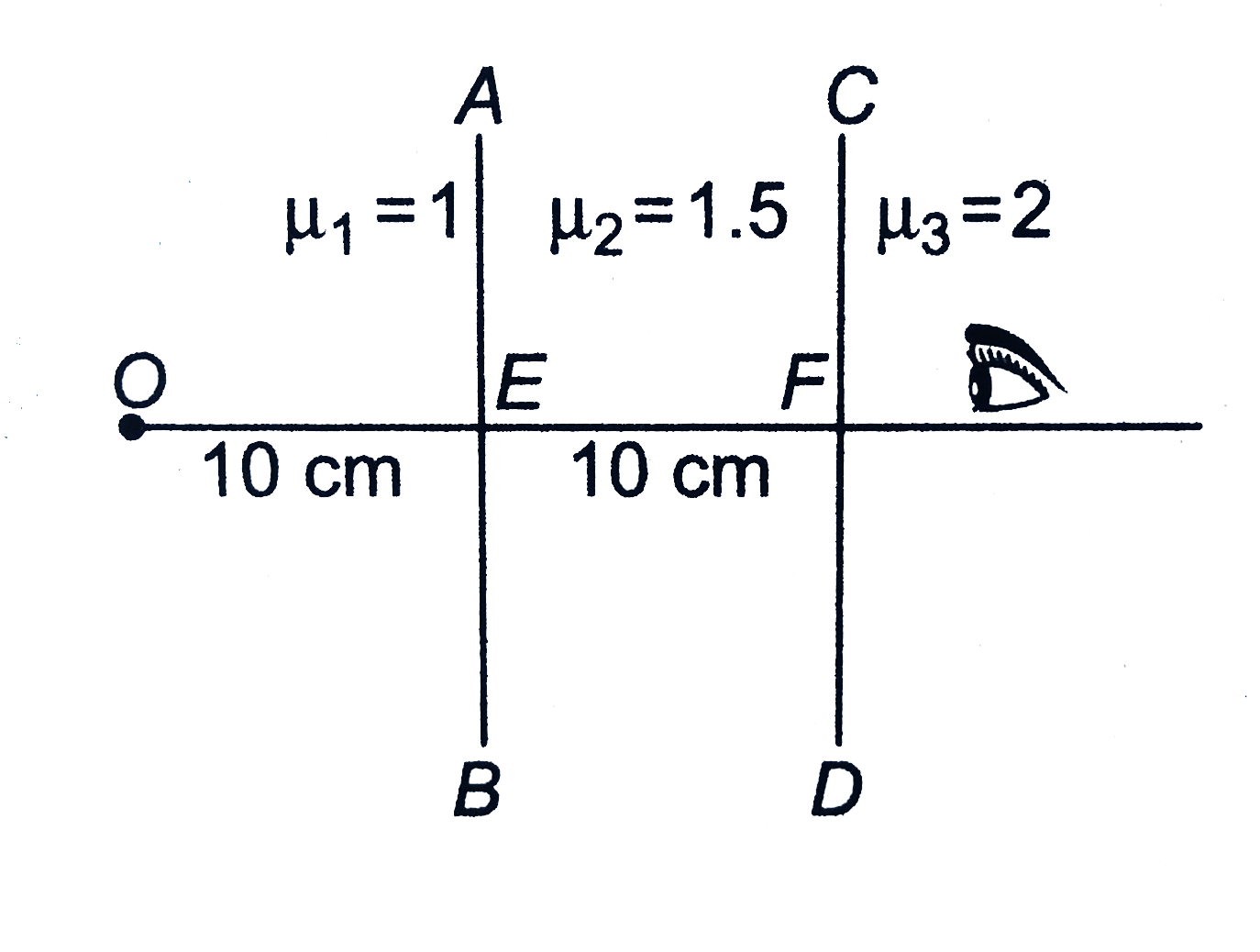
View SolutionA small point object is placed atOat a distance of0.60metre in air from a convex spherical surface of refractive index1.5.If the radius of the curvature is 25cmthen what is the position of the image on the principal axis.
View SolutionA small point objects is placed in air at a distance of 60cm from a convex spherical refractive surface of μ=1.5. If radius of curvature of spherical surface is 25m, calculate the position of the image and the power of the refracting surface.
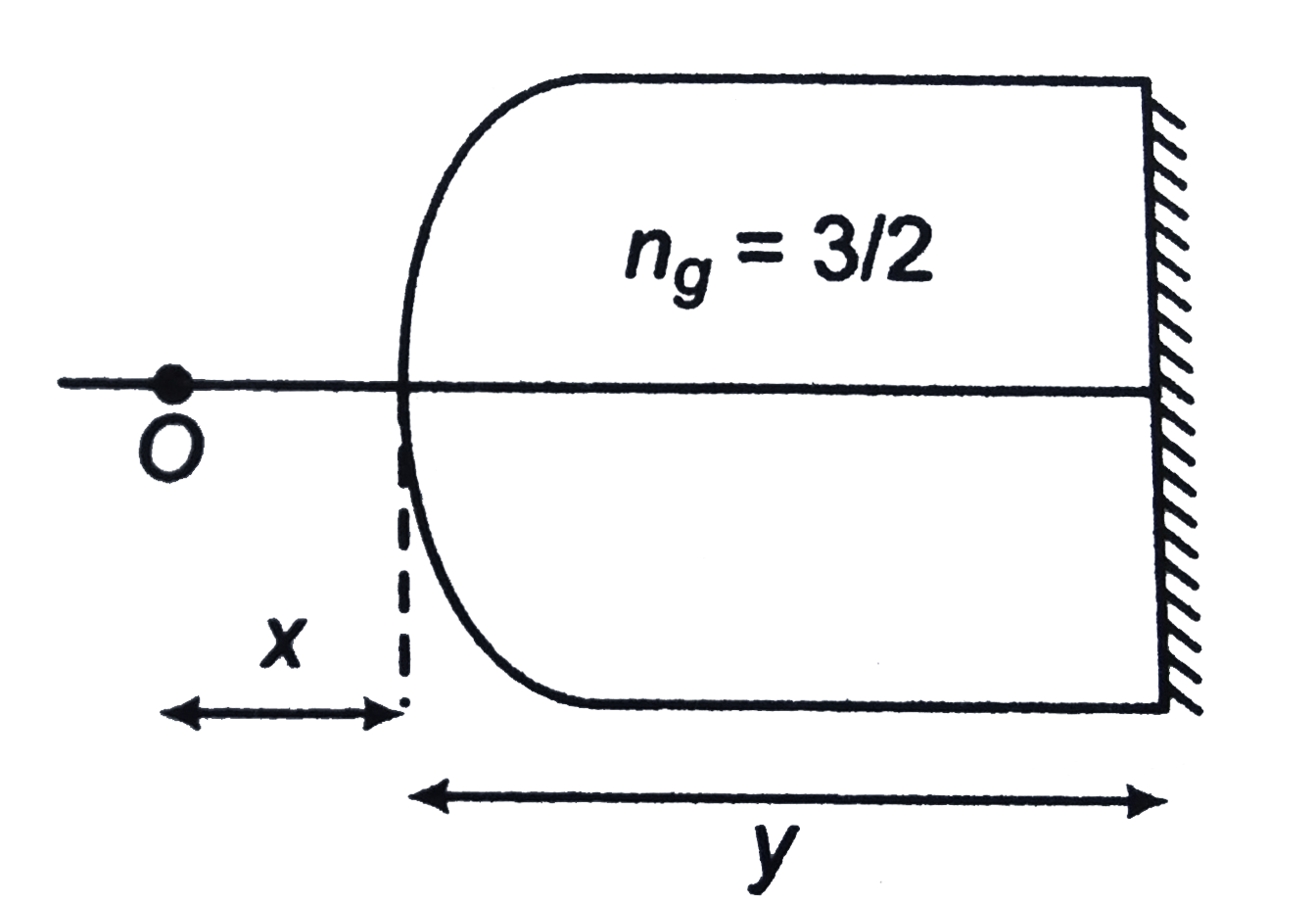
View SolutionIn the figure shown , a point object O is placed in air on the principal axis. The radius of curvature of the spherical surfaces is 60cm. I is the final image formed after all reflections and refractions.
View SolutionTwo refracting media are separated by a spherical interfaces as shown in the figure. AB is the principal axis, μ1andμ2 are the refractive indices of medium of incidence and medium of refraction respectively. Then,
View Solution

