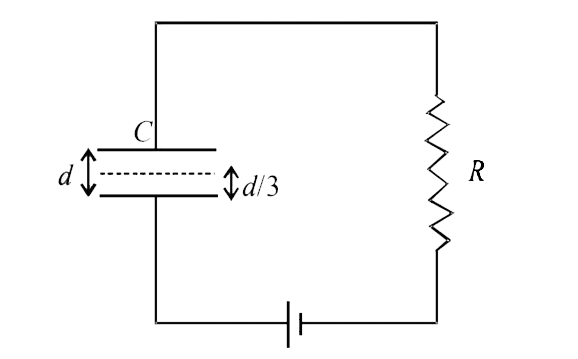
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant $K = 2$ . The level of liquid is $d / 3$ initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-

A

$\frac{6 ε_{0} R}{5 d + 3 V t}$

B

$\frac{(15 d + 9 V t) ε_{0} R}{2 d^{2} - 3 d V t - 9 V^{2} t^{2}}$

C

$\frac{6 ε_{0} R}{5 d - 3 V t}$

D

$\frac{(15 d - 9 V t) ε_{0} R}{2 d^{2} + 3 d V t - 9 V^{2} t^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

a. $C_{e q} = \frac{\frac{2 ε_{0}}{d / 3 - V t} \times \frac{ε_{0}}{2 d / 3 + V t}}{\frac{2 ε_{0}}{d / 3 - V t} + \frac{ε_{0}}{2 d / 3 + V t}} = \frac{6 ε_{0}}{5 d + 3 V t}$
Now $τ = C_{e q} R = \frac{6 ε_{0}}{5 d + 3 V t}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS CURRENT ELECTRICITY

Similar Questions

Knowledge Check

A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant $K = 2$ . The level of liquid is $d / 3$ initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-

A $\frac{6 ε_{0} R}{5 d + 3 / t}$
B $\frac{(15 d + 9 v t) ε_{0} R}{2 d^{3} - 3 d v t - g v^{2} t^{2}}$
C $\frac{6 ε_{0} R}{5 d - 3 v t}$
D $\frac{(15 d - 9 v t) ε_{0} R}{2 d^{3} + 3 d v t - 9 v^{2} t^{2}}$
A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant $K_{1} = 6 and K_{2} = 4$ . New capacitance will be

A $4 \frac{A ε_{0}}{d}$
B $4.8 \frac{A ε_{0}}{d}$
C $5 \frac{A ε_{0}}{d}$
D $2.4 \frac{A ε_{0}}{d}$
A parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?

A $\frac{3 K ε_{0} A}{4 d}$
B $\frac{4 K ε_{0} A}{3 d}$
C $\frac{(K + 1) ε_{0} A}{2 d}$
D $\frac{K (K + 3) ε_{0} A}{2 (K + 1) d}$

Recommended Questions

Home
Ask Doubt
Profile