In the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
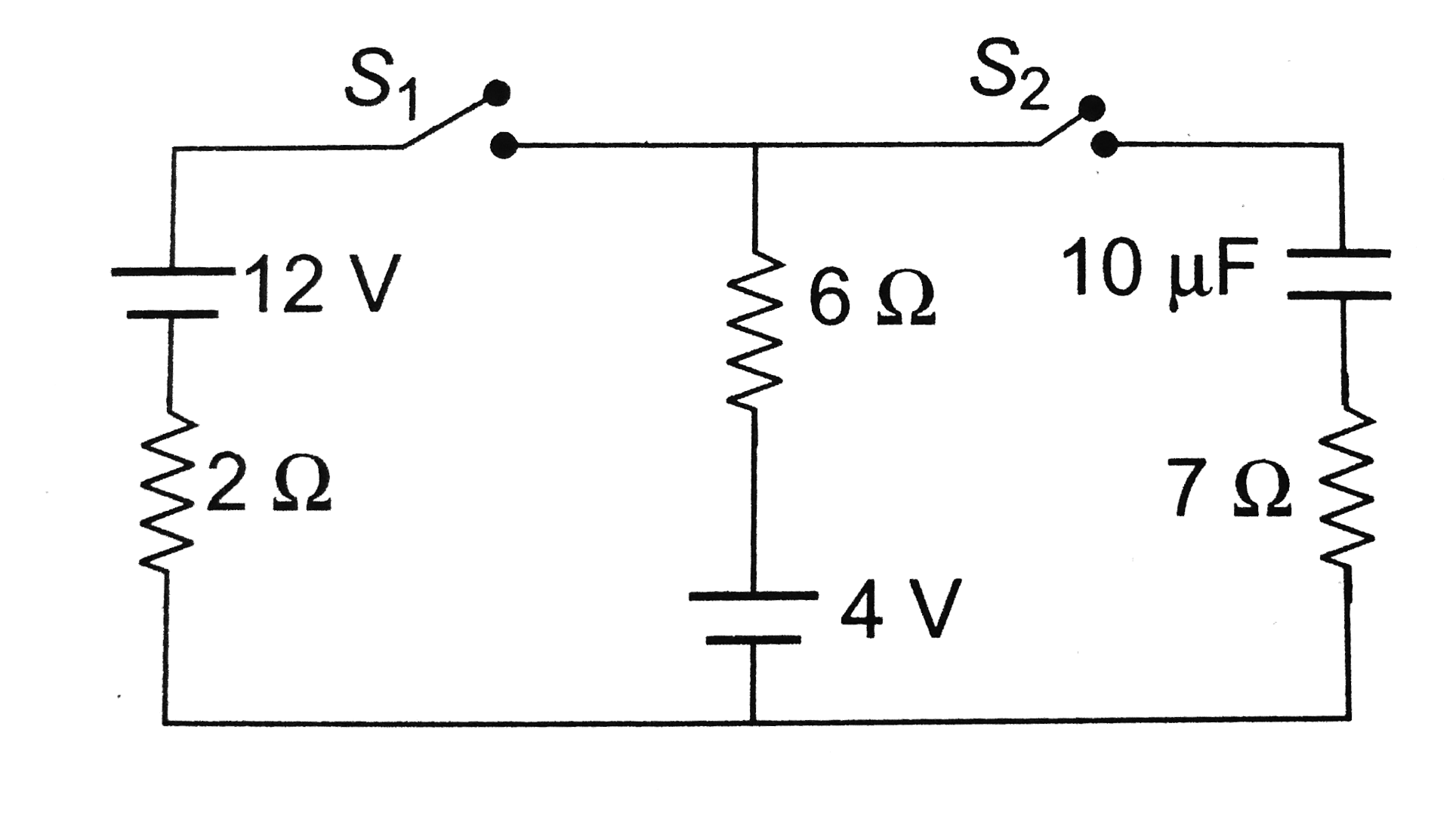
is 100μC
increases to 120μC if one-third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
both a. and b.
charge on the capacitor remains unchanged if one-third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
The correct Answer is:C
c. After long time, current through the capacitor = 0
Therefore, current through the 6Ω resistor, I=(12−4).8=1A
Voltage across capacitor, V=4+(6)(1)=10V
Charge on the capacitor, Q=(10)(10)=100μC
After the insertion of the dielectric, we get
C'=Aε0d3+d3+d3(2)=Aε0d⎡⎣113+13+16⎤⎦
=(10)(1(5/6))=56(10)=12μF
Hence, voltage across the capacitor remains the same.
Charge on the capacitor , Q'=(12)(10)=120μC.
Similar Questions
In the circuit diagram shown in the figure the switches S1 and S2 are closed at time t=0.After time t=(0.1)ln2sec, switch S2 is opened.The current in the circuit at time t=0.2n2sec is equal to x32amp.Find out value of x.
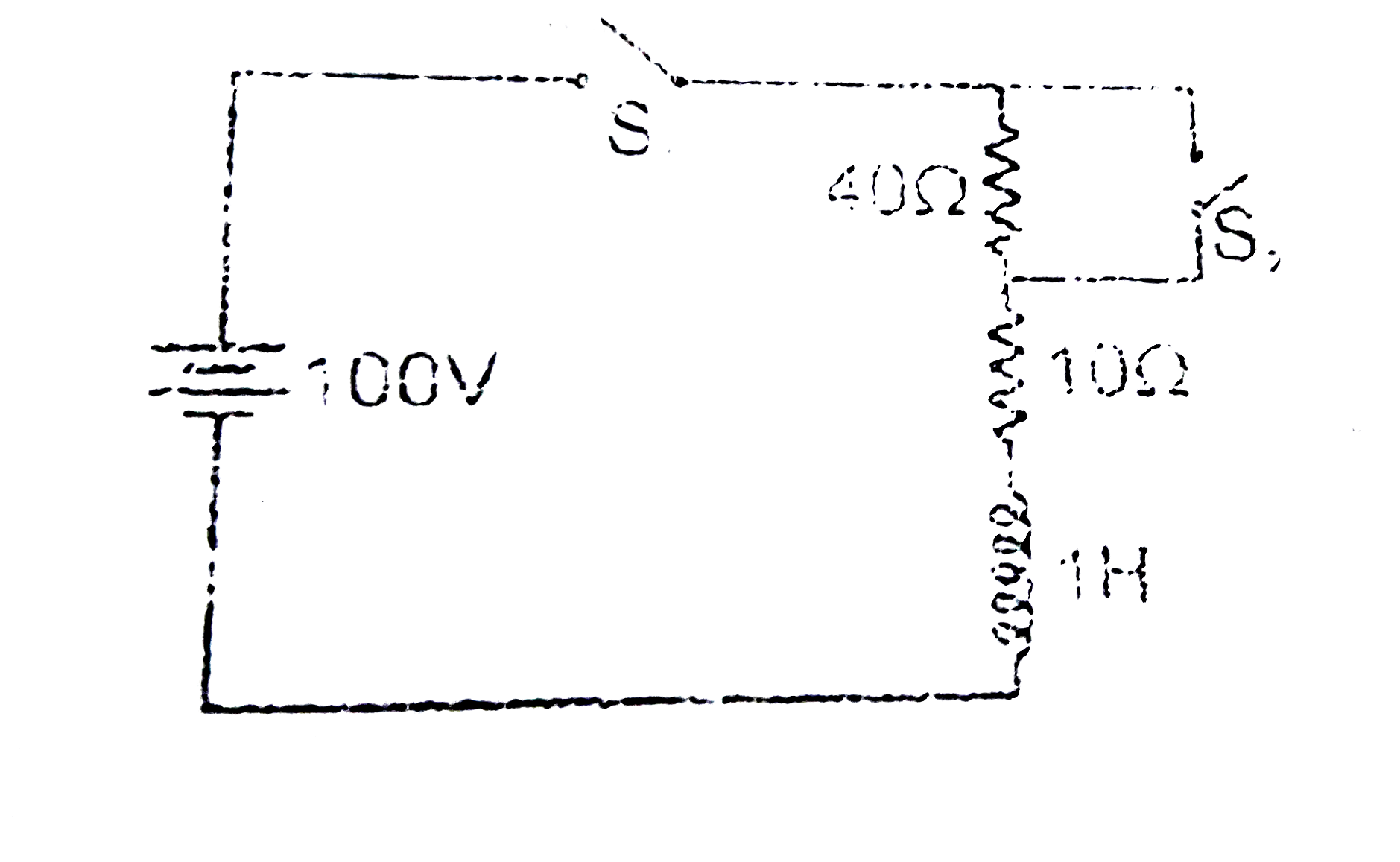
View SolutionIn circuit shown in figure-5.149 if switches S1 and S2 are closed at t=0, find the oscillation frequency of charge in this circuit. Neglect mutual induction between inductors.

View Solution
Knowledge Check
In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
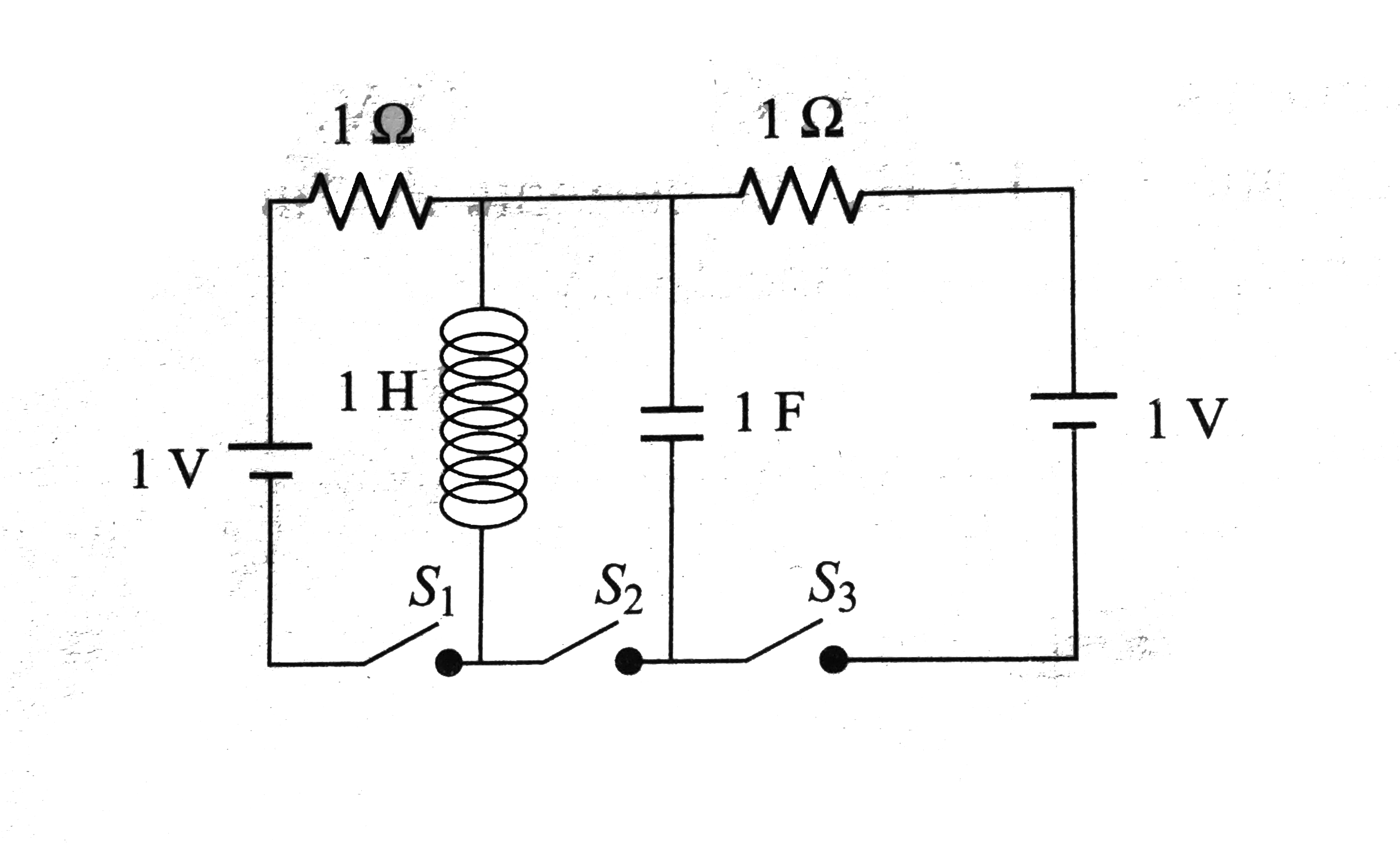
the maximum charge on the capacitorA√3(1+1e)B√3(1−1e)C√2(1+1e)D√2(1−1e)In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
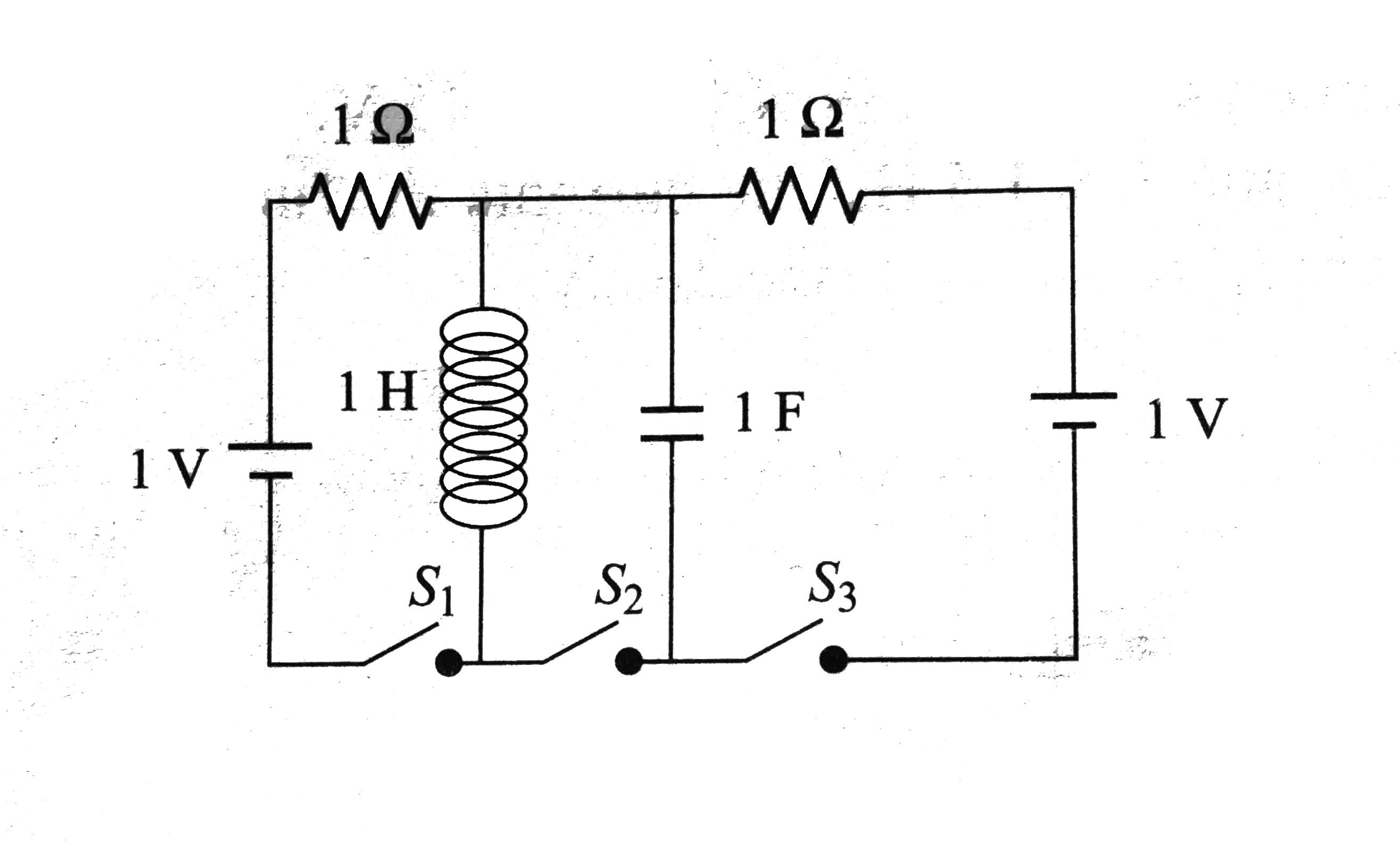
the charge on the upper plate of the capacitor as a funtion of timeA√2(1−1e)sin(t+3π4)B√2(1−1e)sin(t+π4)C√3(1−1e)sin(t+π4)D√3(1+1e)sin(t+π4)In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
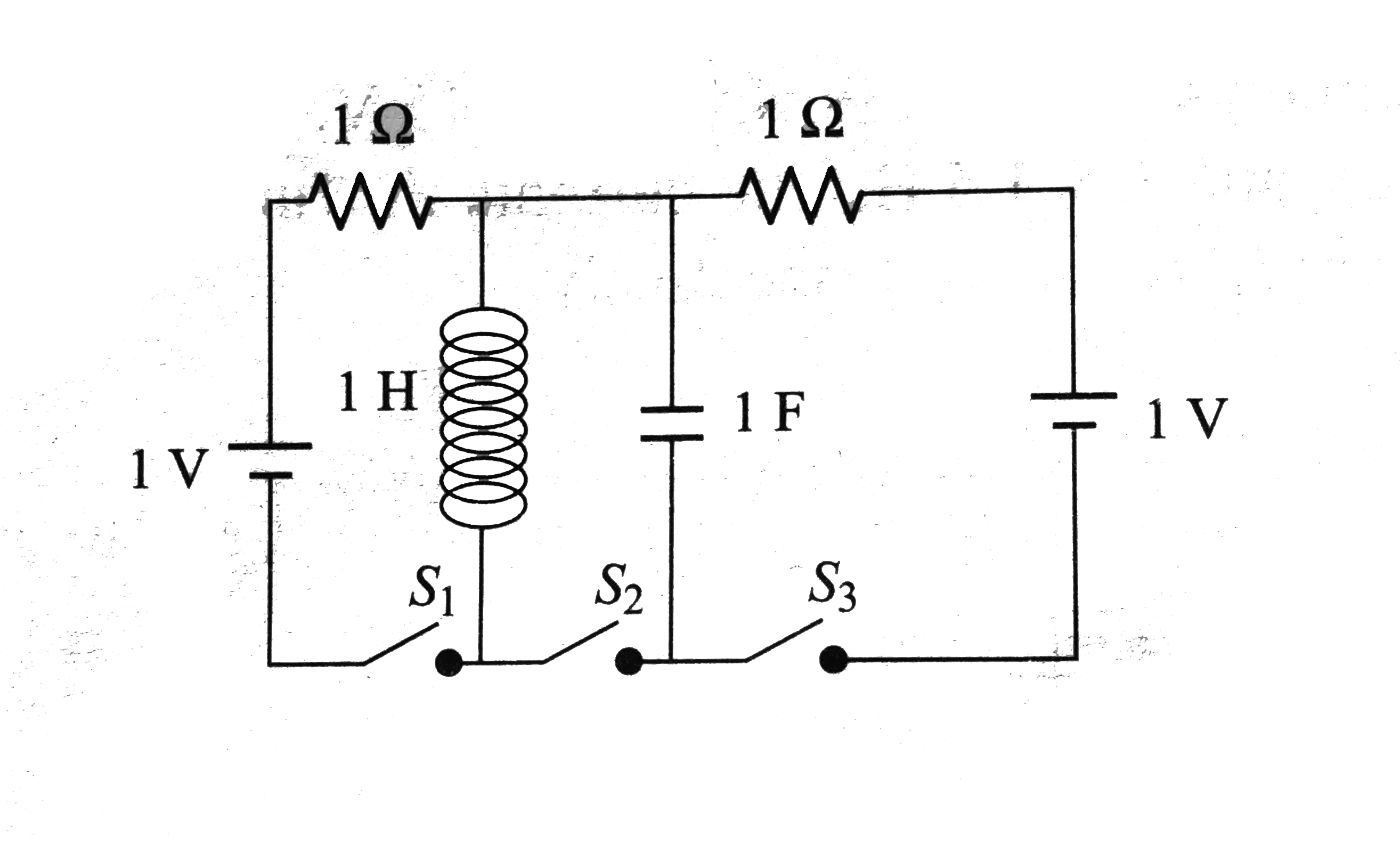
the maximum current in the circuit containing inductor and capacitor (only S2 is closed)A√3(1−1e)B√2(1−1e)C√3(1+1e)D√2(1+1e)
In the circuit shown switches S1 and S2 have been closed for 1sec and S2 remained open.Just after 1 second is over switch S2 is closed and S1,S3 are opened.Find after that instant The charge on the upper plate of the capacitor as function of time taking the instant of switching on of S2 and switching off all time switches to be t=0 is q=x×10−2cos(t+π4).Findout value of x.

View SolutionIn the circuit shown below, the switch S is connected to position P for a long time so that the charge on the capacitor become q1μC. The S is switched to psition Q. After a long time, the charge on the capacitor is q2μC. The magnitude of q1 is

View SolutionIn the circuit shown below, the switch S is connected to position P for a long time so that the charge on the capacitor become q1μC. The S is switched to psition Q. After a long time, the charge on the capacitor is q2μC. The magnitude of q2 is

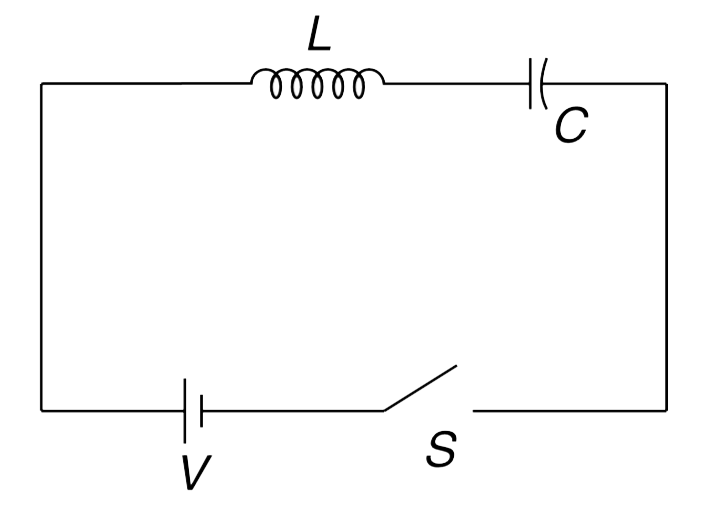
View SolutionIn the circuit shown in the figure, switch S is closed at time t=0.
(a) Write current in the circuit and charge on capacitor as a function of time. Draw the graphical plot for the same.
(b) Find maximum charge on the capacitor. What is potential difference across the inductor when charge on the capacitor is maximum?
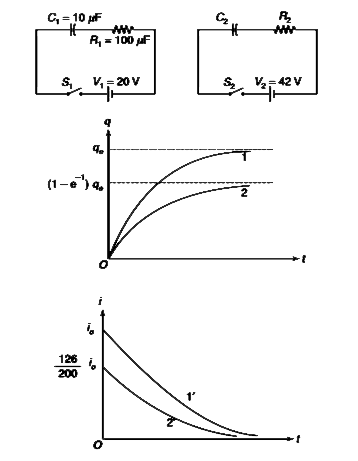
View SolutionConsider two circuits given below. When switches S1andS2 are closed at t=0, the charge on capacitors C1 and C2 change with time as shown in graph 1 and 2 respectively. The current i1 and i2 in the two circuits change as shown in graph 1' & 2' respectively. Write the variation of current in the second circuit as function of time after the switch is closed at t=0.e−1=0.37
View Solution
