A nonconducting sphere with a cavity has volume charge density ρ. O1andO2 represent the two centers as shown. The electric fields inside the cavity is E0. Now, an equal and opposite charge is given uniformly to the sphere on its outer surface. The magnitude of electric field inside the cavity becomes

zero
E0
2E0
3E0
The correct Answer is:B
Electric field will remains the same, because electric field due to surface charge distrinuted uniformly will be zero at any point inside the sphere.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type
109 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Knowledge Check
A conductor with a cavity is charged positively and its surface charge density is σ. If E and V represent the electric field and potential, then inside the cavity
AE = 0 and V = 0BE = 0 and σ- constantCV = 0 and σ = constantDE = 0 and V = constantThe electric field inside a spherical shell of uniform surface charge density is
AZeroBConstantCProportional to the distance from the centreDIrregularA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is
 Aρ3ε0→dBρ3ε0(→r−→d)Cρ3ε0(→d−→r)Dρ3ε0(→r)
Aρ3ε0→dBρ3ε0(→r−→d)Cρ3ε0(→d−→r)Dρ3ε0(→r)
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionFind the electric field at the center of the sphere due to the induced charges on the surface of the sphere, as shown in Fig. 22-30.

View SolutionA solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
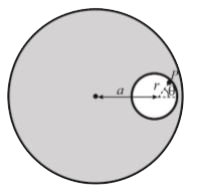
View SolutionIntensity of electric field inside a uniformly charged hollow sphere is
View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View Solution
