A wire of linear charge density λ passes through a cuboid of length l, breadth b and height h(lgtbgth) in such a manner that the flux through the cuboid is maximum. The position of the wire is now changed, so that the flux through the cuboid is minimum. The raito of maximum flux to minimum flux will be
√l2+b2h
√l2+b2+h2h
h√l2+b2
h√l2+b2+h2
The correct Answer is:B
From gauss's law ϕ=qε0
So, ϕmaxϕmin=QmaxQmin=λ(l2+b2+h2)1/2λh
=√l2+b2+h2h
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Multiple Correct Answer type
Explore 109 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Assertion and Reason Type
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:CENGAGE PHYSICSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Question Bank
Explore 4 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
Similar Questions
An infinite wire having charge density λ passes through one of the edges of a cube having edge length l.
a. Find the total flux passing through the cube.
b. Find the flux passing through the surfaces in contact with the wire.
c. Find the flux passing through the surfaces not in contact with the wire.

View SolutionLinear charge density of wire is 8.85 μC/m Radius and height of the cylinder are 3m and 4 m. Then find the flux passing through the cylinder :-
View Solution
Knowledge Check
An infinite wire having charge density λ passes through one of the edges of a cube having length l. find the total flux passing through the cube
 Aλlε0Bλl4ε0Cλl6ε0DNone of these
Aλlε0Bλl4ε0Cλl6ε0DNone of theseA: When the magnetic flux through a loop is maximum, induced emf is maximum.
R: When the magnetic flux through a loop is minimum, induced emf is minimum.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion.BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion.CIf Assertion is true statement but Reason is false.DIf both Assertion and Reason are false statements.Twelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
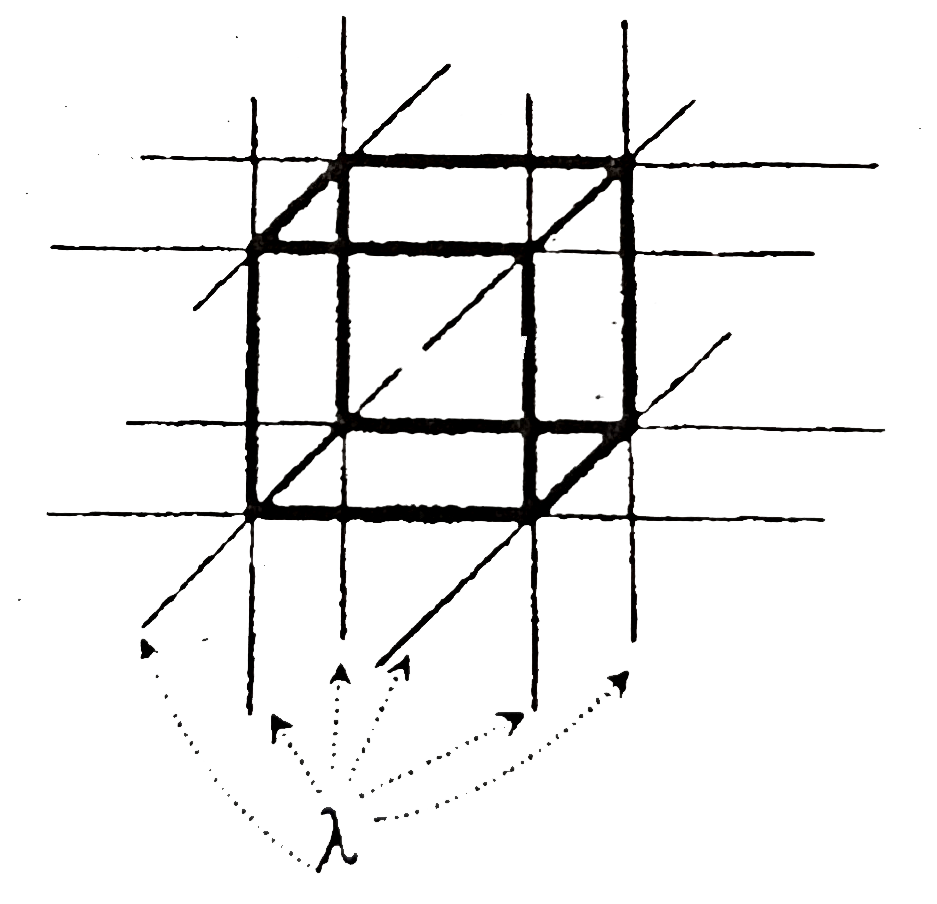 A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)
A(λl2ε0)B(λlε0)C(λl3ε0)D(3λlε0)
A long strikes with a charge of λ per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cyclinder. What will be the effect on the flux passing through curved surface if the portions of the line charge outside the cyclinder is removed

View SolutionA long string with a charge of a per unit length passes through an imaginary cube of edge L. The maximum possible flux of electric field through the cube will be
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
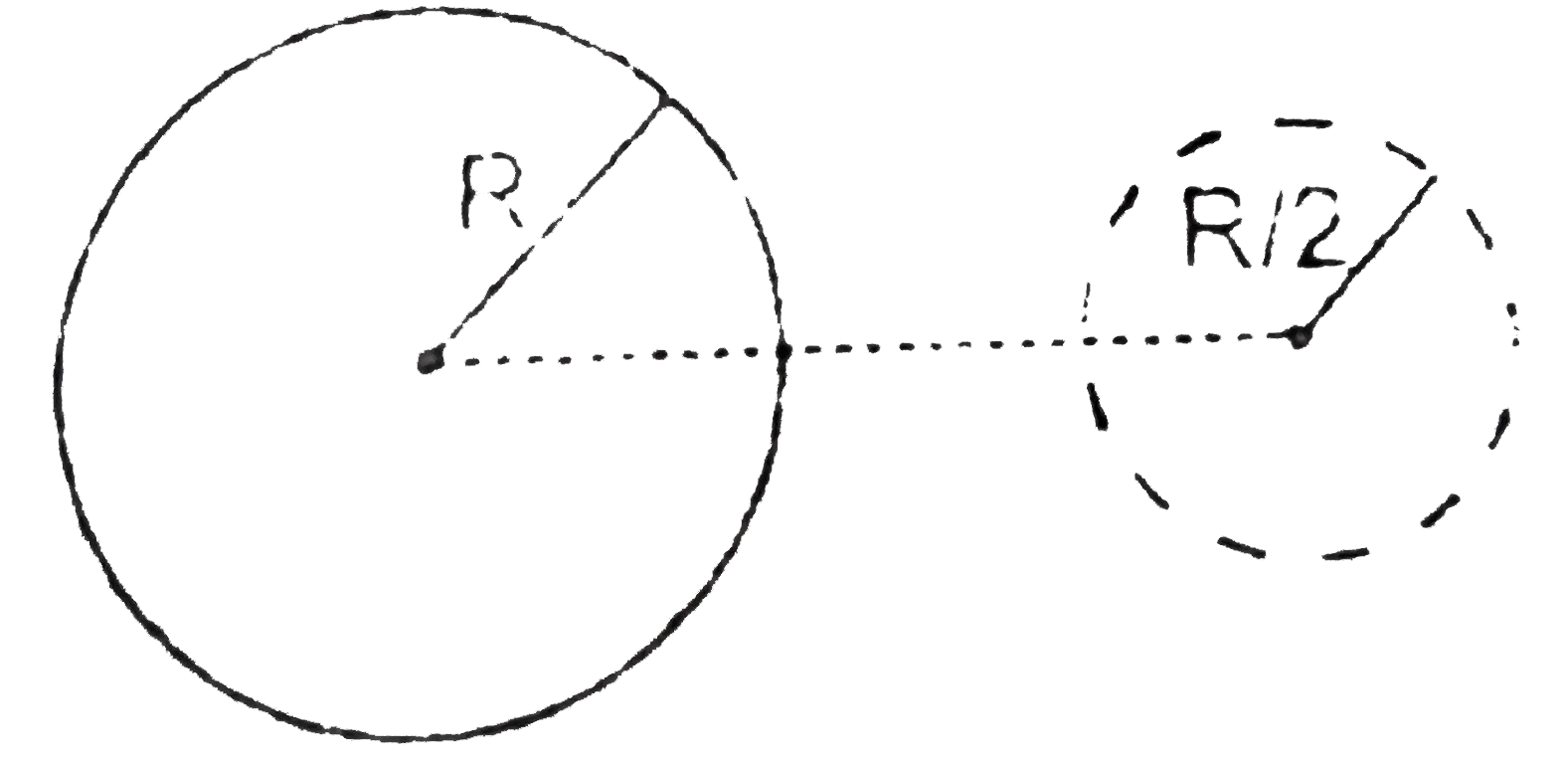
View Solutiona point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
View Solution