An element with emfε and interval resistance r is connected across an external resistance R. The maximum power in external circuit is 9W. The current flowing through the circuit in these conditions is 3A. Then which of the following is // are correct ?
ε=6V
r=R
r=1Ω
r=3Ω
The correct Answer is:A, B, C
Current through the circuit is I=ε/(r+R).
Power dissipated in external resistance is
P=I2R=ε2(r+R)2R
We know that power dissipated is maximum when r=R.
Pmax=ε2r(2r)2=ε24r=9W,i=ε2r=3A
Solve to get , ε=6Vandr=1Ω.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning
6 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Comprehension
13 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct
60 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Concept Based
9 Videos
Similar Questions
A battery of emf E and internal resistance r is connected is to external resistance B The maximum point is the external circuit is 9W The current flowing in the circuit under the condition is 3A What is the value of E in volt ?
View SolutionIn the circuit, the current flowing through 10Ω resistance
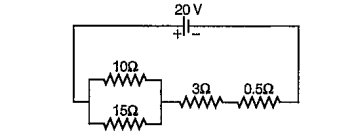
View Solution
Knowledge Check
A cell of internal resistance r connected across an external resistance R can supply maximum current when
AR=rBR>rCR=r2DR=0An external resistance R is connected to a cell of internal resistance r. The current in the circuit is maximum when
AR<rBR>rCR=rDR=2rFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
A2E4r+RB3E4r+RC3E3r+RD2E3r+R
A cell of emf ε and internal resistance (r) is connected in series with an external resistance (nr) then the ratio of the terminal potential difference to emf is:
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
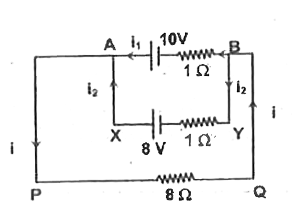
View SolutionAn total resistance R is connected to a cell of internal resistance r the maximum current flows in the external resistance, when
View SolutionIn the circuit, the current flowing through 10Ω resistance is
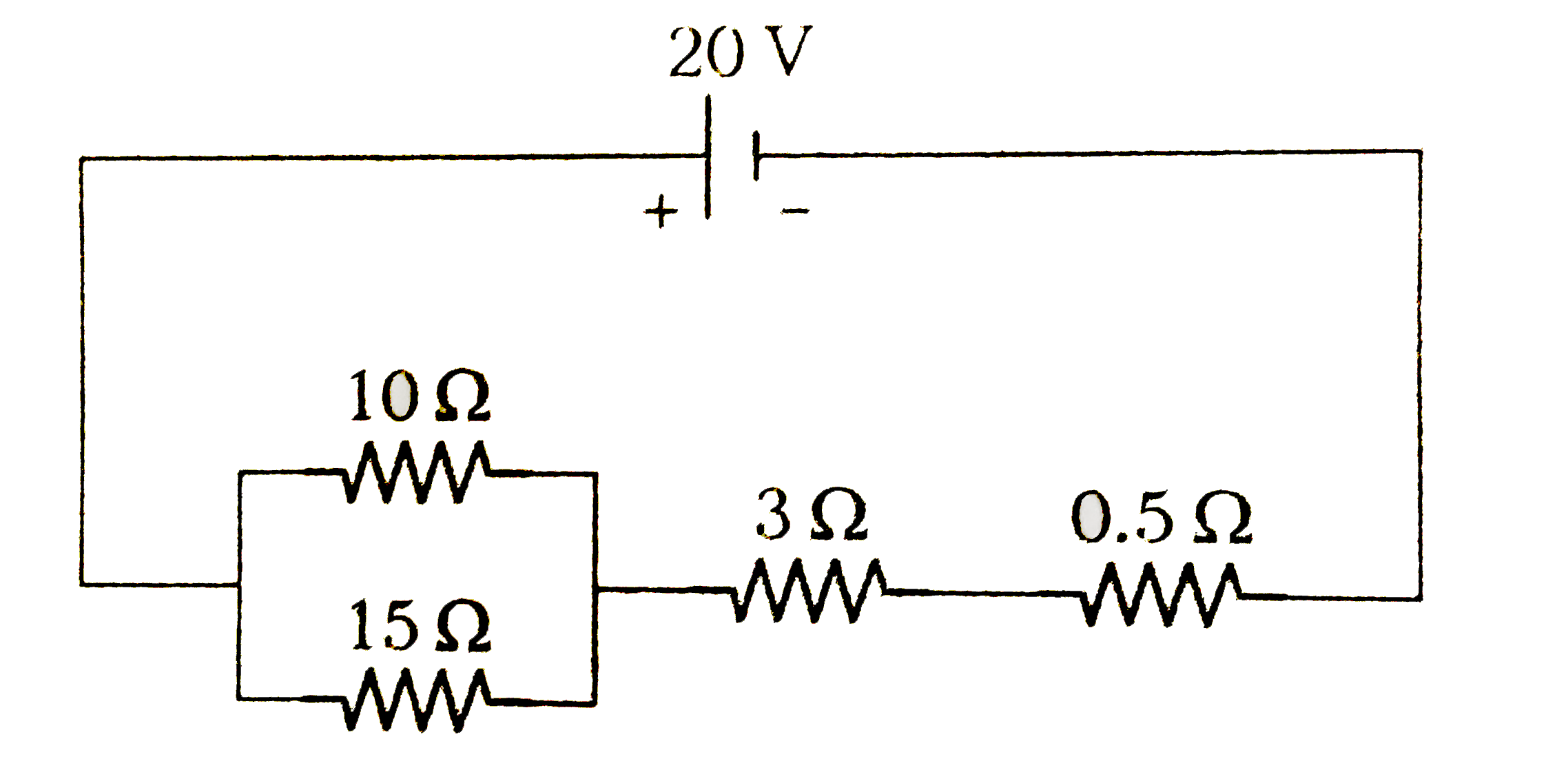
View SolutionA cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is
View Solution
