In the gives circuit, a meter bridge is shows in a balanced state. The bridge wire has a resistance of 1Ωcm−1. Find the value of the unknown resistance X and the current draws from the battery of negligible internal resistance.

The correct Answer is:4Ω,0.66A
For the balanced bridge, the ratio of the two resistances is equal to the ratio of the lengths of the two parts AJ and JB of the wire, i.e.,
X6Ω=40cm60cm or X=4Ω
No current flows through the galvanometer G. The resistances of the parts AJ and JB are 40Ω and 60Ω, respectively. If R is the equational resistance between the point A and B, then we have
1R=1(X+6)Ω+1(40+60)Ω
or R=10011Ω
i=VR=6V(100/11)Ω=0.66A
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:Single Correct
Explore 94 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:Multiple Correct
Explore 7 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:Exercise 6.1
Explore 15 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
- ELECTROMAGENTIC INDUCTIONBook:CENGAGE PHYSICSChapter:ELECTROMAGENTIC INDUCTIONExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
In the circuit a meter bridge a shown in the balanced state .The meter bridge wire has a resistance of 1Ω/cm. Calculate the unknown resistance Y and the current drawn from the battery of negiligible internal resistance
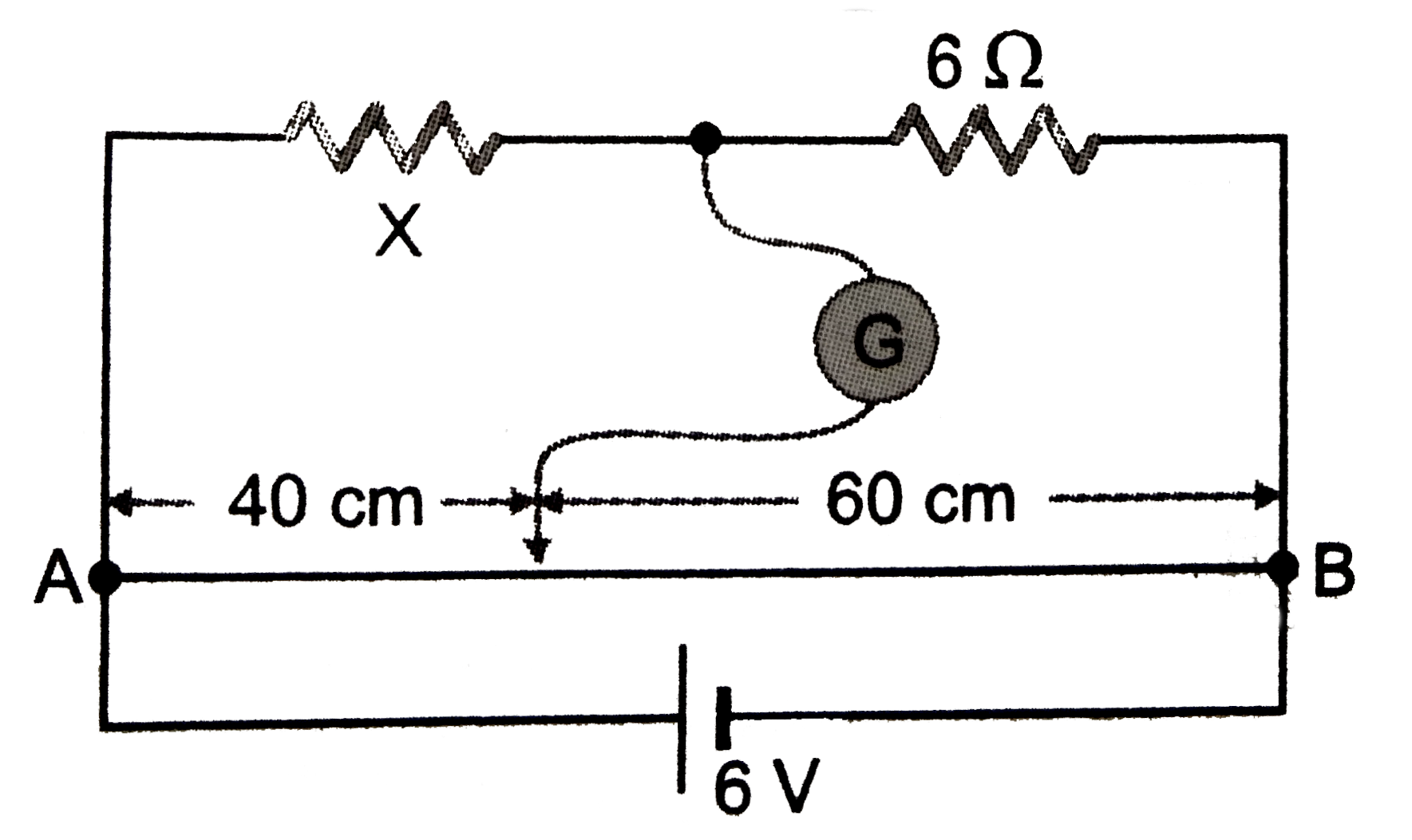
View SolutionIn the following circuit, a metre bridge is shown in its balanced state. The metre bridge wire has a resistance of 1 ohm/cm. calculate the value of the unknown resistance X and the current drawn from the battery of negligible internal resistance.
View Solution
Knowledge Check
In the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is
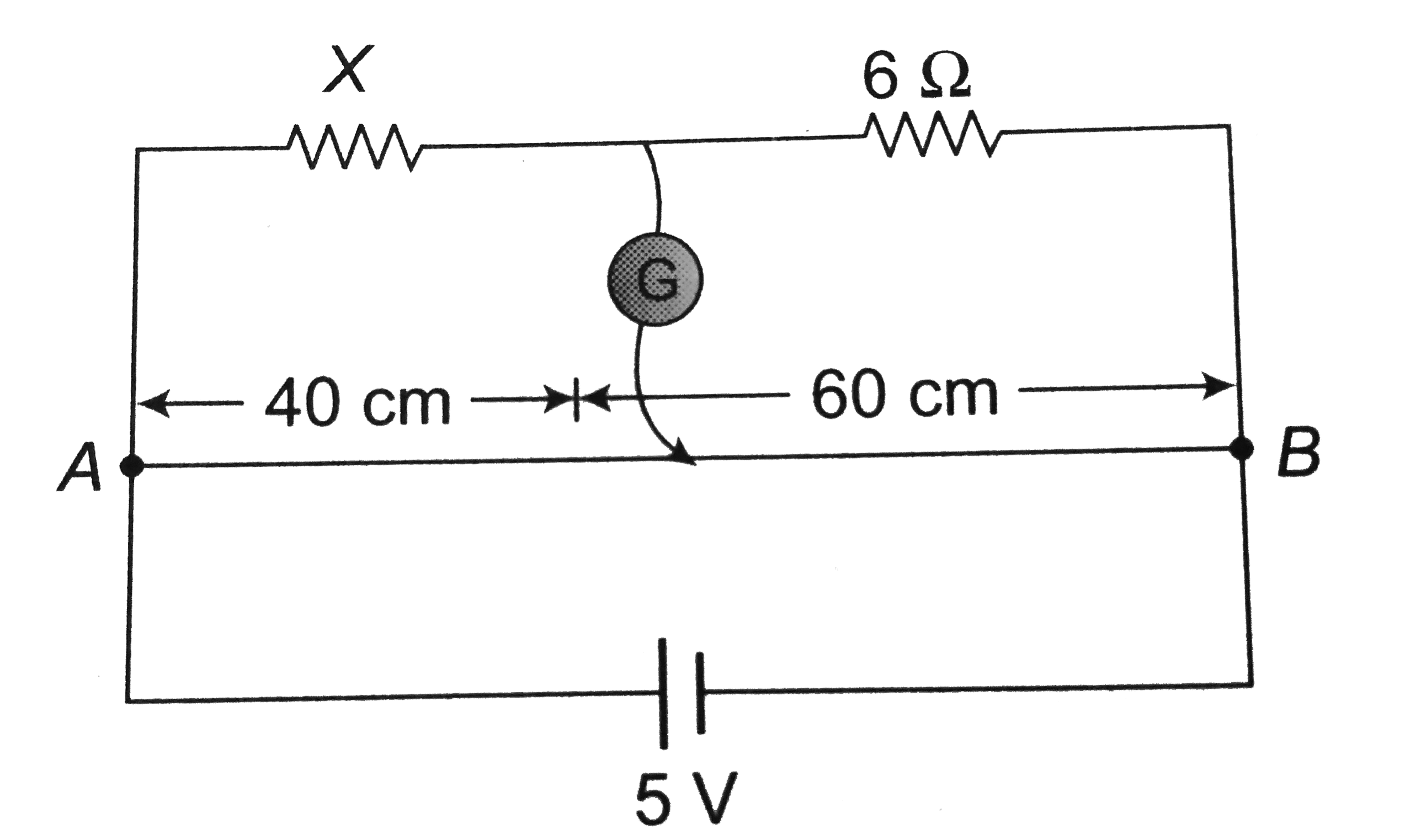 A6Ω,5ampB10Ω,0.1ampC4Ω,1.0ampD12Ω,0.5amp
A6Ω,5ampB10Ω,0.1ampC4Ω,1.0ampD12Ω,0.5ampIn a balanced metre bridge, the segment of wire opposite to a resistance of 70Ω is 70 cm. The unknown resistance is
A30ΩB60ΩC90ΩD15ΩIn a meter bridge the null point is obtained at the middle point of the wire. If in one gap the resistance is 10Ω, then the value of resistance in the other gap is :–
A10ΩB5ΩC15ΩD500Ω
In the given circuit a bridge is shown in the balanced state.The meter bridge wire has a resistance of 1Ωcm−1 .Calculate the unknown resistance X and the current drawn from the battery of negligible internal resistence. If the magnitude the position of galvanometer and the cell, how it will affect the position of the galvanometer ?

View Solution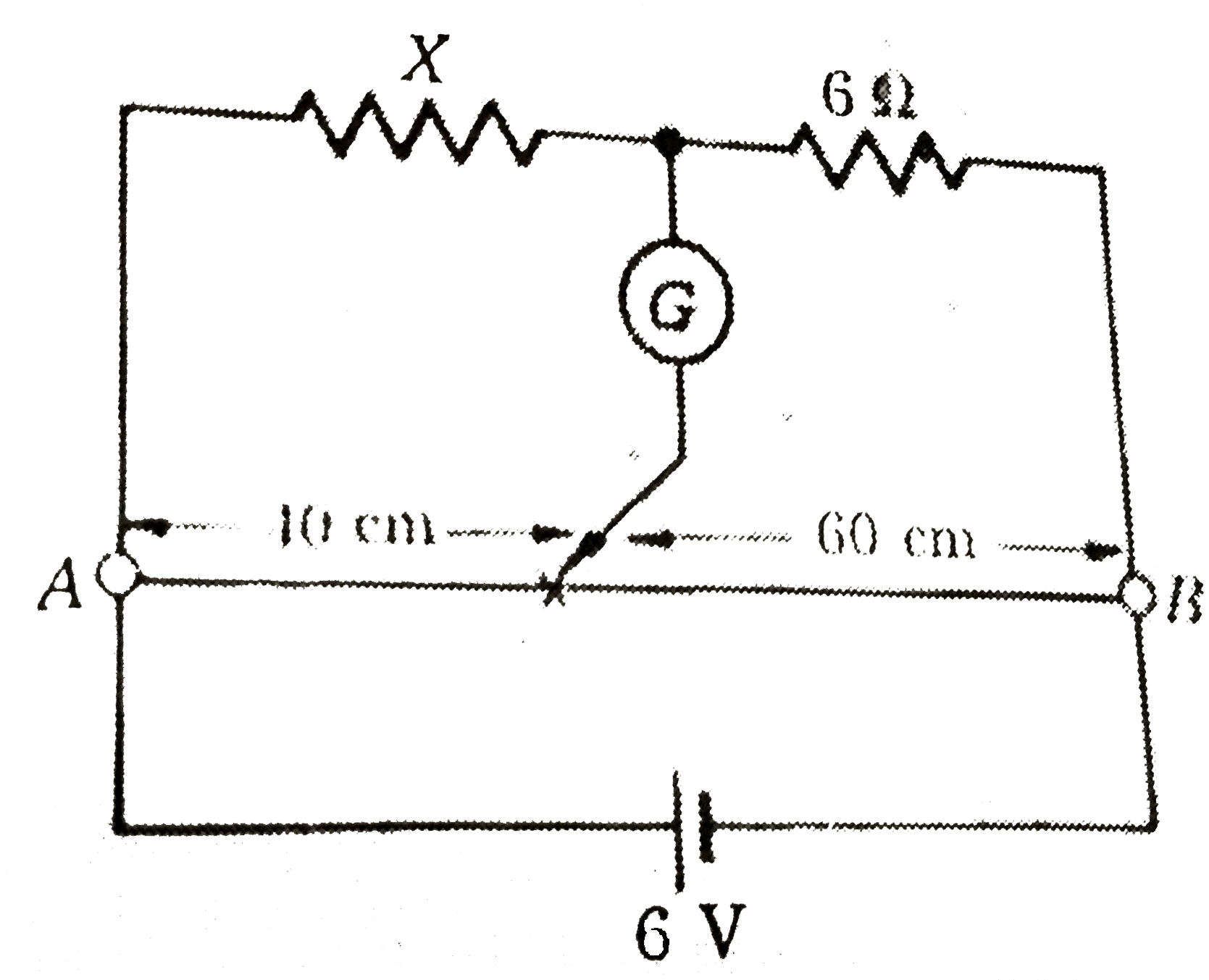
In the circuit shown in figure. A metre bridge is shown in its balanced state. The metre bridge wire has a resistance of a 4 ohm/cm. calculate the value of the unknown resistance X and the current drawn from the battery of negligible resistance.
View SolutionIn the circuit shows in Fig. 6.20, a meter bridge is in its balance state. The meter bridge wire has a resistance of 1Ωcm−1. Calculate the value of the unknow resistance X and the battery of negligible internal resistance.
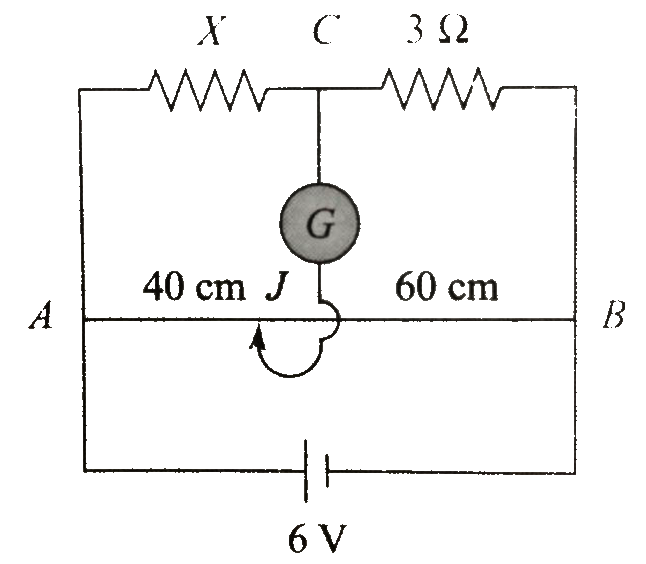
View SolutionIn the circuit of meter bridge shown in the figure.If null deflection is obtained at 40cm length of the wire as shown,the value of unknown resistance is
View SolutionIn a meter bridge , the balancing length from left end ( standard resistance of one ohm is in the right gap ) is found to be 20 cm . The value of the unknow resistance is .
View Solution

