In the given circuit
E1=3E2=2E3= 6 volts R1=2R4=6Ω
R3=2R2=4Ω C=5μf.
Find the current in R and the energy stored in the capacitor.
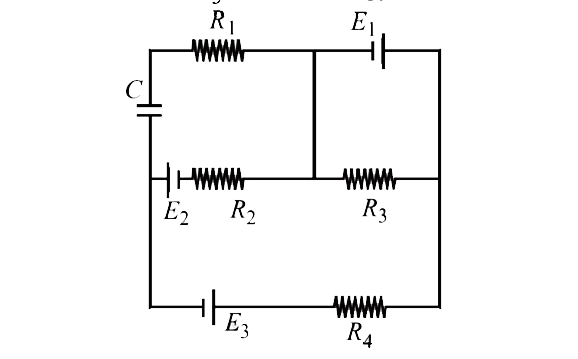
Applying Kirchhoff's law in ABFGA
6−(i1+i2)4=0(i)
Applying Kirchhoff's law in BCDEFB
i2×3−3−2+2i2+(i2+i1)4=0(ii)
Putting the value of 4(i1+i2)=6inEq.(ii), we get
3i2−5+2i2+6=0ori2=−15
Substituting this value in Eq. (i) we get
i1=1.5−(−15)=1.7A
Therefore, current in R3isi1+i2=1.5A. To find the potentail
differece across the capacitor, we have
VE−2−0.2×2=VG
or VE−VG=2.4V
Therefore, energy stored in capacitor is
12CV2=12×5×10−6×(2.4)2=1.44×10−5J
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
In the given circuit
E1=3E2=2E3=6vo<sR1=2R4=6ohms
R3=2R2=4ohmsC=5μf.
Find the current in R and the energy stored in the capacitor.

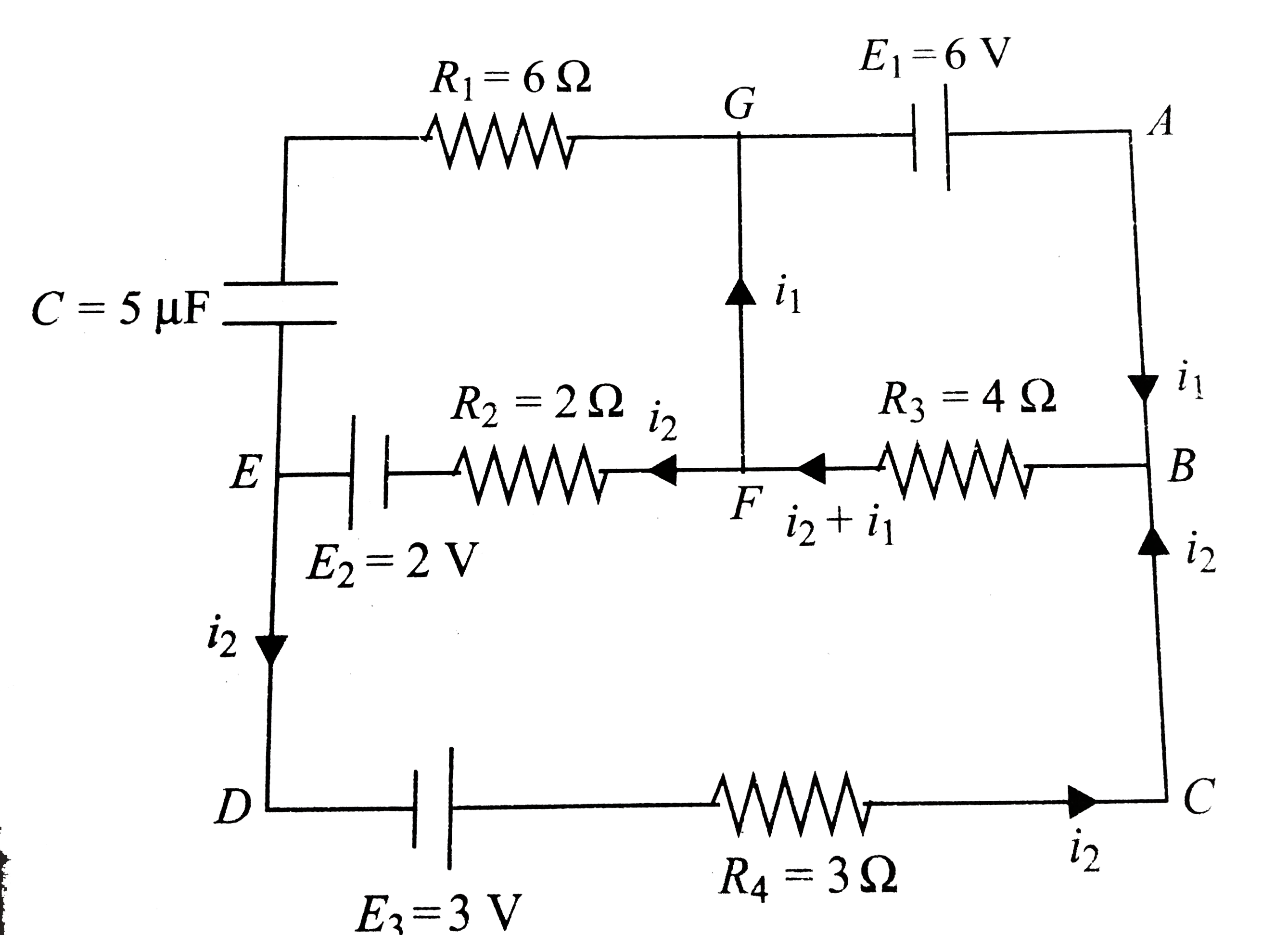
View SolutionIn the given circuit. E1=6vo<s,E2=2vo<s,E3=6vo<s
R1=6ΩR2=2ΩR3=4Oemga,R4=3Ω and C=5μF. Find the current in R3 and energy stored in the capacitor at steady state
View Solution
Knowledge Check
In Fig, E=5 volt , r=1Ω,R2=4Ω,R1=R3=1Ω and C=3μF. Then the numbercal value of the charge on each plate of the capacitor is
 A24μCB12μCC6μCD3μC
A24μCB12μCC6μCD3μCIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
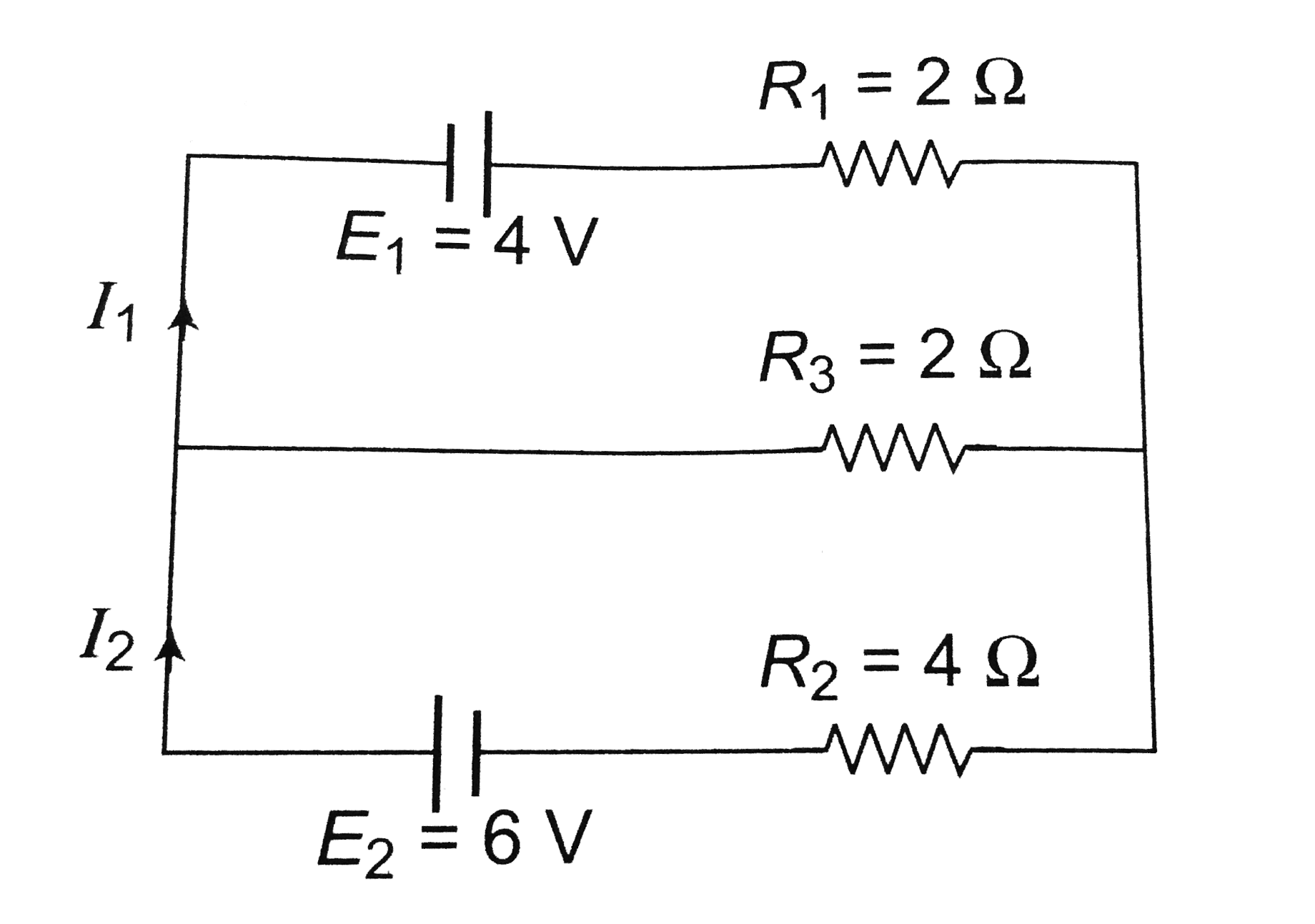 A1.6AB1.8AC1.25AD1.0A
A1.6AB1.8AC1.25AD1.0AIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
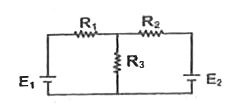 A0.083333333333333B3.5 AC1.75 ADnone of these
A0.083333333333333B3.5 AC1.75 ADnone of these

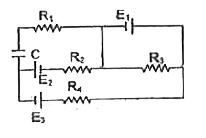
In the circuit shown in figure. ε1=3,ε2=2,ε3=6V,R1=2,R4=6Ω,R3=2,R2=4ΩandC=5μF. Find the current in the resistor R3 and the electrical energy stored in the capacitor C.
View SolutionIn the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Oemga,andR3=4Ω. Find the currents i1andi2
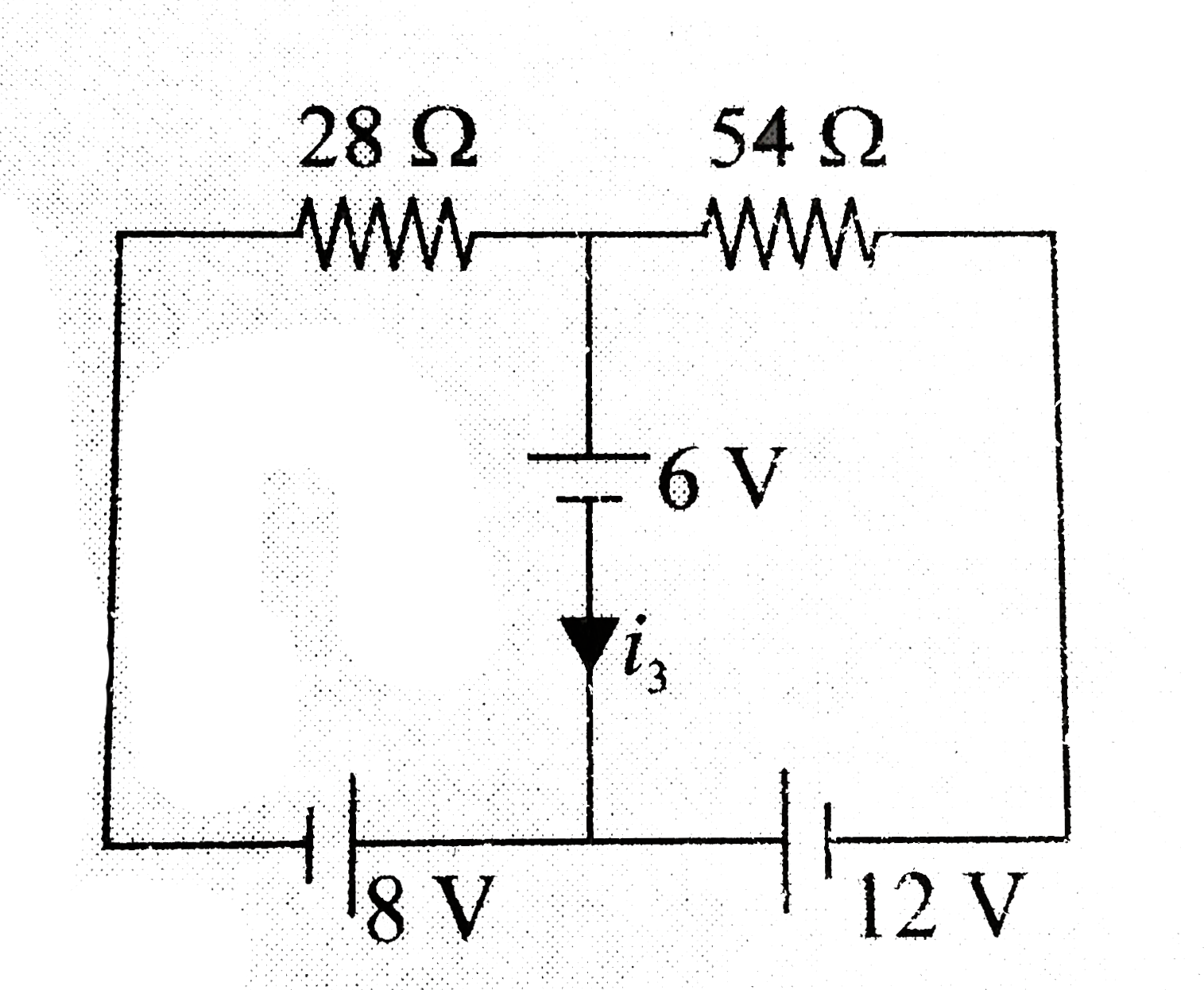
View SolutionIn the circuit shown in fig E1=3vo<s,E2=2vo<s,E3=1vo<andR=r1=r2=r3=1ohm.
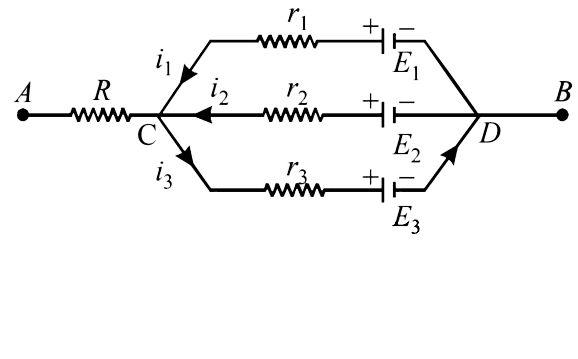
(i) Find the potential difference between the points A and B and the currents through each branch.
(ii) If r2 is short circuited and the point A is connected to point B, find the current through E1,E2,E3 and the resistor R.
View SolutionIn the circuit shown in fig. 5.265, E1=E2=E3=2V and R1=R2=4Ω. The current flowing between points A and B through battery E2 is
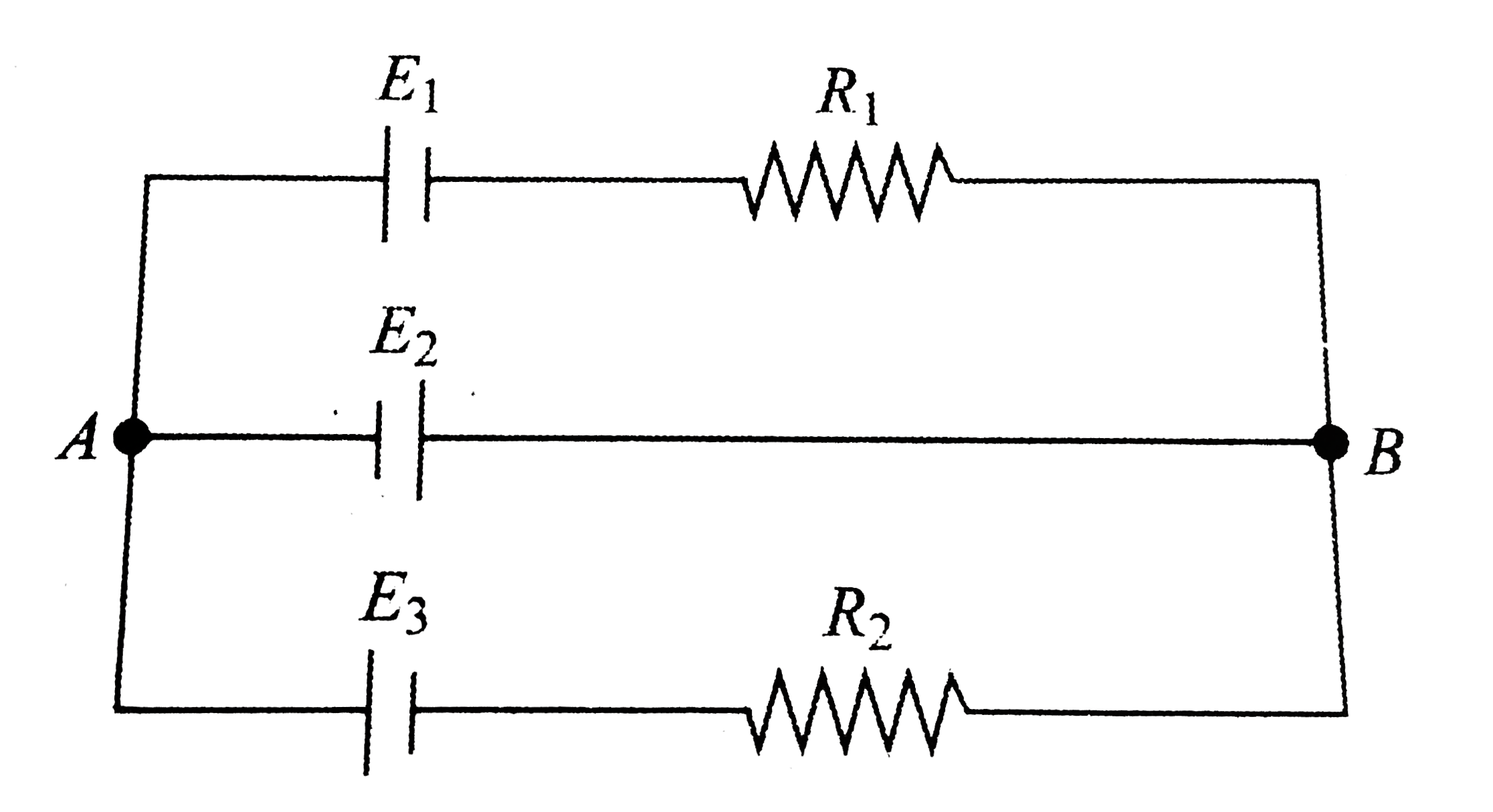
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3

View Solution