n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
E/n
E/nr
nE/r
0
The correct Answer is:D
To find the potential difference across any one cell in a series circuit consisting of n identical cells, each with an EMF (E) and internal resistance (r), we can follow these steps:
Step 1: Understand the Total EMF and Total Internal Resistance
When n cells are connected in series, the total EMF (E_total) of the circuit is the sum of the EMFs of all the cells. Therefore, the total EMF is given by:
Etotal=n⋅E
The total internal resistance (R_total) of the circuit is the sum of the internal resistances of all the cells. Hence, the total internal resistance is:
Rtotal=n⋅r
Step 2: Apply Ohm's Law
In a series circuit, the total current (I) flowing through the circuit can be calculated using Ohm's Law. The total voltage (E_total) is equal to the current (I) multiplied by the total resistance (R_total):
Etotal=I⋅Rtotal
Substituting the expressions for E_total and R_total:
nE=I⋅(nr)
Step 3: Solve for Current (I)
From the equation above, we can solve for the current (I):
I=nEnr=Er
Step 4: Find the Potential Difference Across One Cell
The potential difference (V) across one cell can be found using the formula:
V=E−I⋅r
Substituting the value of I from Step 3:
V=E−(Er)⋅r
This simplifies to:
V=E−E=0
Step 5: Correcting the Approach
However, we need to account for the fact that the potential difference across one cell in the circuit is actually:
V=E−I⋅r
Substituting the current (I) we found:
V=E−(Er)⋅r=E−E=0
This indicates that the potential difference across one cell is not zero, but rather:
V=E−En=E(n−1)n
Final Result
Thus, the potential difference across any one cell in the series circuit is:
V=E(n−1)n
When n cells are connected in series, the total EMF (E_total) of the circuit is the sum of the EMFs of all the cells. Therefore, the total EMF is given by:
Etotal=n⋅E
The total internal resistance (R_total) of the circuit is the sum of the internal resistances of all the cells. Hence, the total internal resistance is:
Rtotal=n⋅r
In a series circuit, the total current (I) flowing through the circuit can be calculated using Ohm's Law. The total voltage (E_total) is equal to the current (I) multiplied by the total resistance (R_total):
Etotal=I⋅Rtotal
Substituting the expressions for E_total and R_total:
nE=I⋅(nr)
From the equation above, we can solve for the current (I):
I=nEnr=Er
The potential difference (V) across one cell can be found using the formula:
V=E−I⋅r
Substituting the value of I from Step 3:
V=E−(Er)⋅r
This simplifies to:
V=E−E=0
However, we need to account for the fact that the potential difference across one cell in the circuit is actually:
V=E−I⋅r
Substituting the current (I) we found:
V=E−(Er)⋅r=E−E=0
This indicates that the potential difference across one cell is not zero, but rather:
V=E−En=E(n−1)n
Thus, the potential difference across any one cell in the series circuit is:
V=E(n−1)n
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Four cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
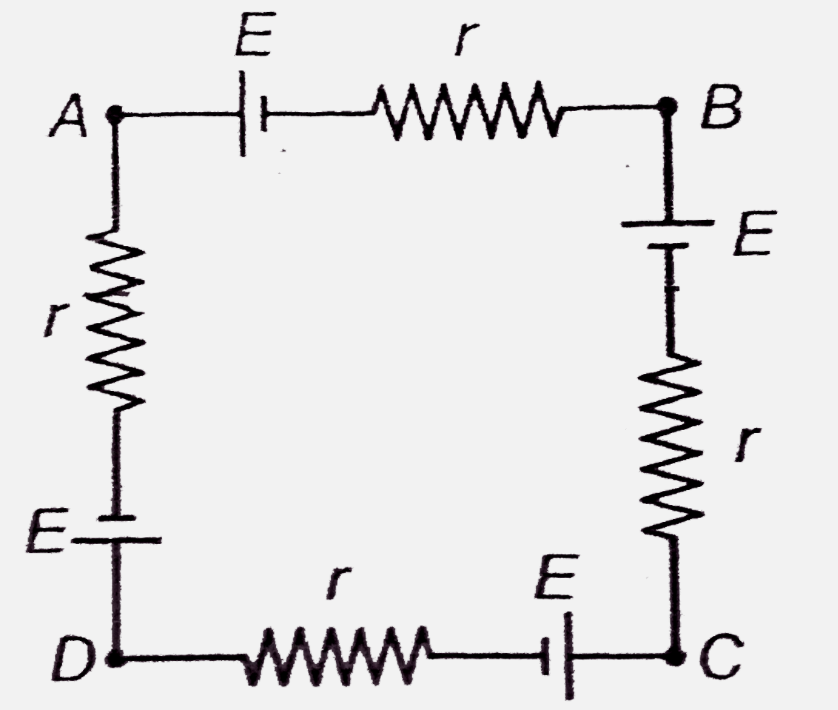
View Solution(a) The emf of a cell is E and its intenal resistance is r. Its terminals are connected to a resistance R. The potential difference between the terminal is 12V if R=3Ω and 16V if R=8Ω. Find the values of E and r
(b) When an unknown resistance is connected across a series combination of two identical cells, each of 18V, current through the resistance is 4A. When it is connected across a parallel combination of the same cells, the current through it is 3A. Find the unknown resistance and internal resistance of each cell.
( c) p identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. One cell (X) is joined with reversed polarity. Find the potential difference across each cell except X and also across X.
(d) 12 cells each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. This battery is connected in series with an ideal ammeter and two cells of same emf as of 12 cells. The current is 3A when the cells and the battery aid each other and 2A when the cells and battery oppose each other. How many cells in the battery are wrongly connected ?
View Solution
Knowledge Check
n identical cells each of emfe and internal resistance r are joined in series so as to form a closed circuit. The P.D. across any one cell is
AzeroBεCε/nDn−1nεTend identical cells each of potential E and internal resistance r are connected in series to form a closed circuit. An ideal voltmeter connected across three cells, will read
A10EB3EC13ED7En identical cells, each of emf ε and internal resistance r, are joined in series to form a closed circuit. One cell A is joined with reversed polarity. The potential difference across any one cell is
AzeroBεCεnDn−1nε
Five identical cells, each of emf E and internal resistance r, are connected in series to form (a) an open (b) closed circuit. If an ideal voltmeter is connected across three cells, what will be its reading ?
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to from a loop. The terminal voltage across each cell is
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to from a closed circuit. One cell a is joined with reversed polarity. The potential difference across each cell, except A, is
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to from a closed circuit. One cell A is joined with reversed polarity. The potential difference across each cell, except A, is
View Solution

