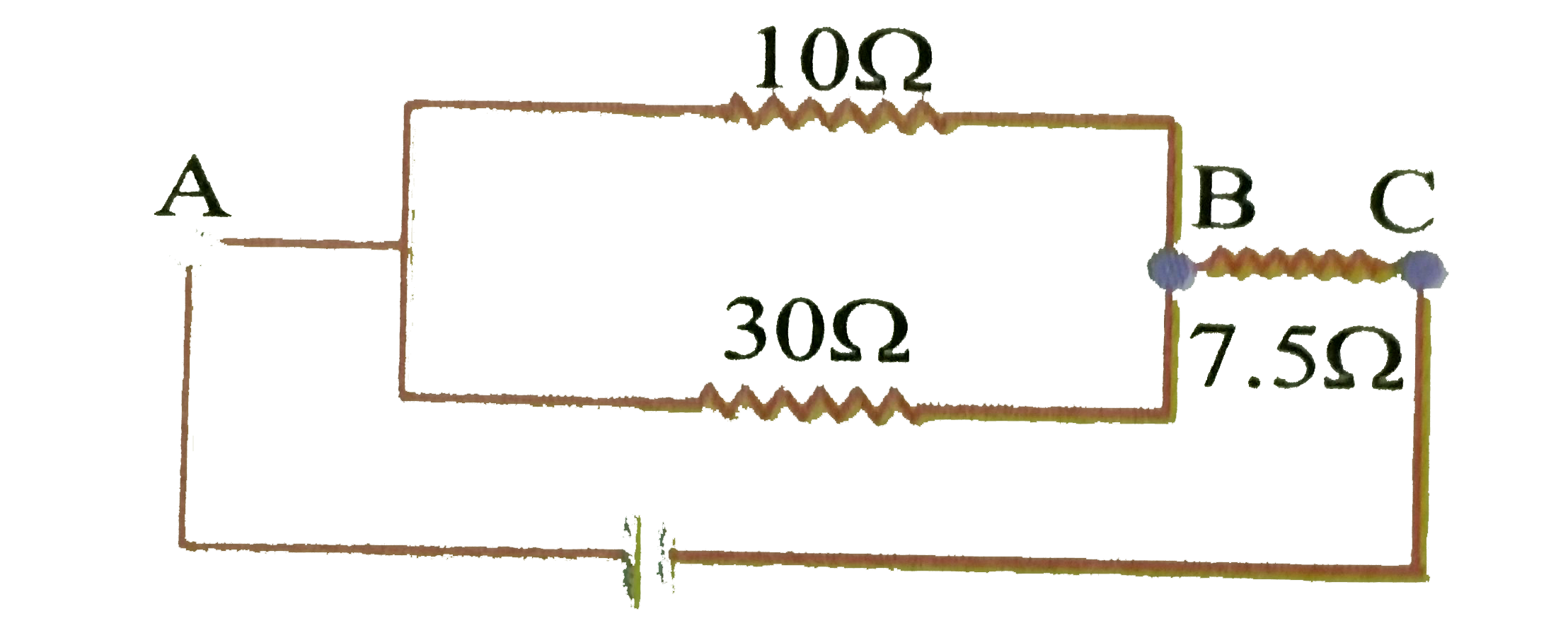In Fig.5.52, the resistances are connected as shown. Given R1=10ΩR2=20Ω. Determine the equivalent resistance between points (i) A and D and (ii) B and C

Video Solution
Text Solution
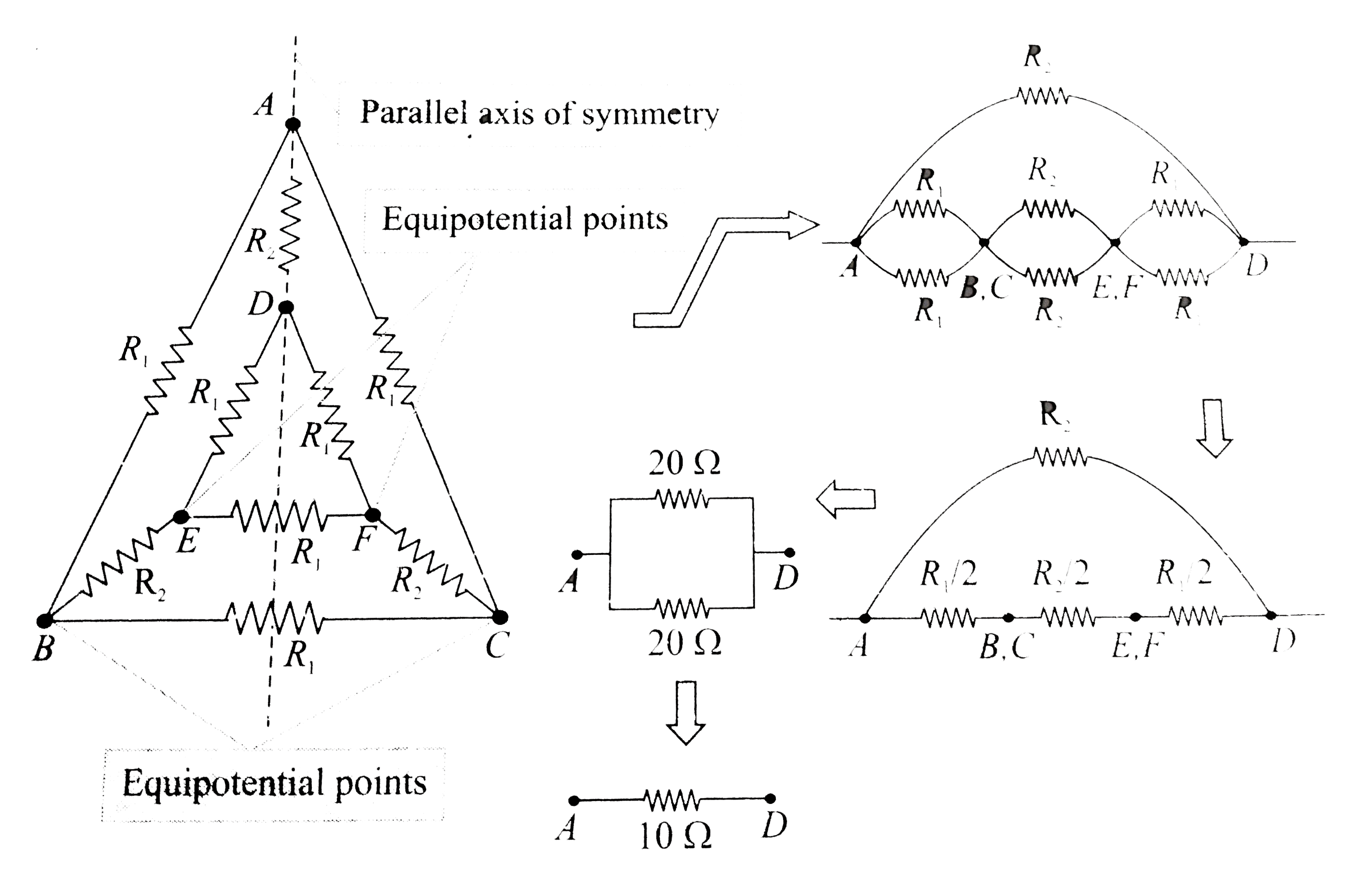
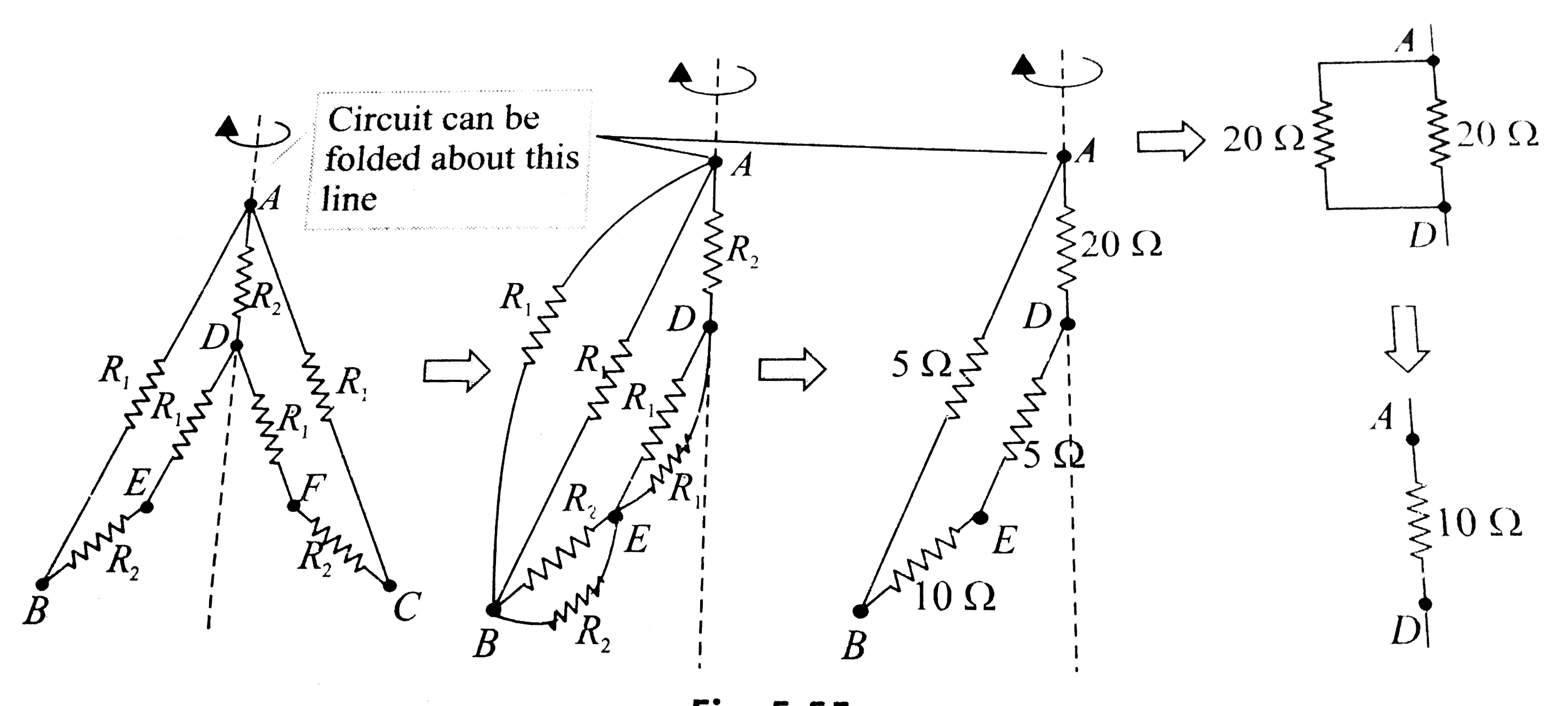
(i) Calculation of equivalent between A and D:
There exists parallel axis of symmetry. The points across the
parallel axis of symmetry can be treated as equipotntial points.
Mehod 1: Points B and C, and E and F are at the same
potential, so the circuit can be redrawn as shown in fig. 5.23.
Thus, the equivalent resistance is 10Ω
Method 2: the points with charge symmetrical to parallel axis
are equipotential points. The resistances connected between
these points can be removed. A step- by-step procedure for the
calculation of equivalent resistance is shown in Fig. 5.54
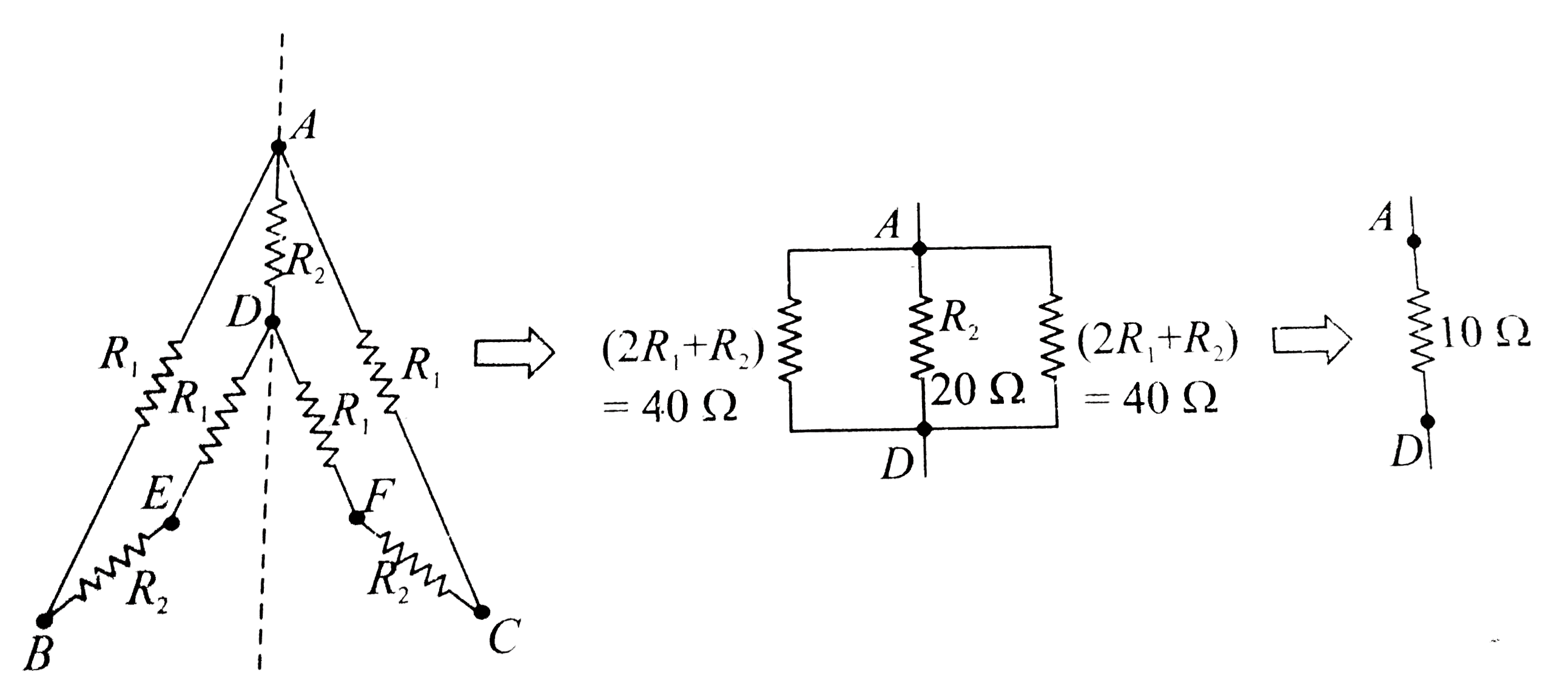
Method 3: We can fold the circuit about the parallel axis of
symmetry. The step -by - step procedure is shown in Fig. 5.55.
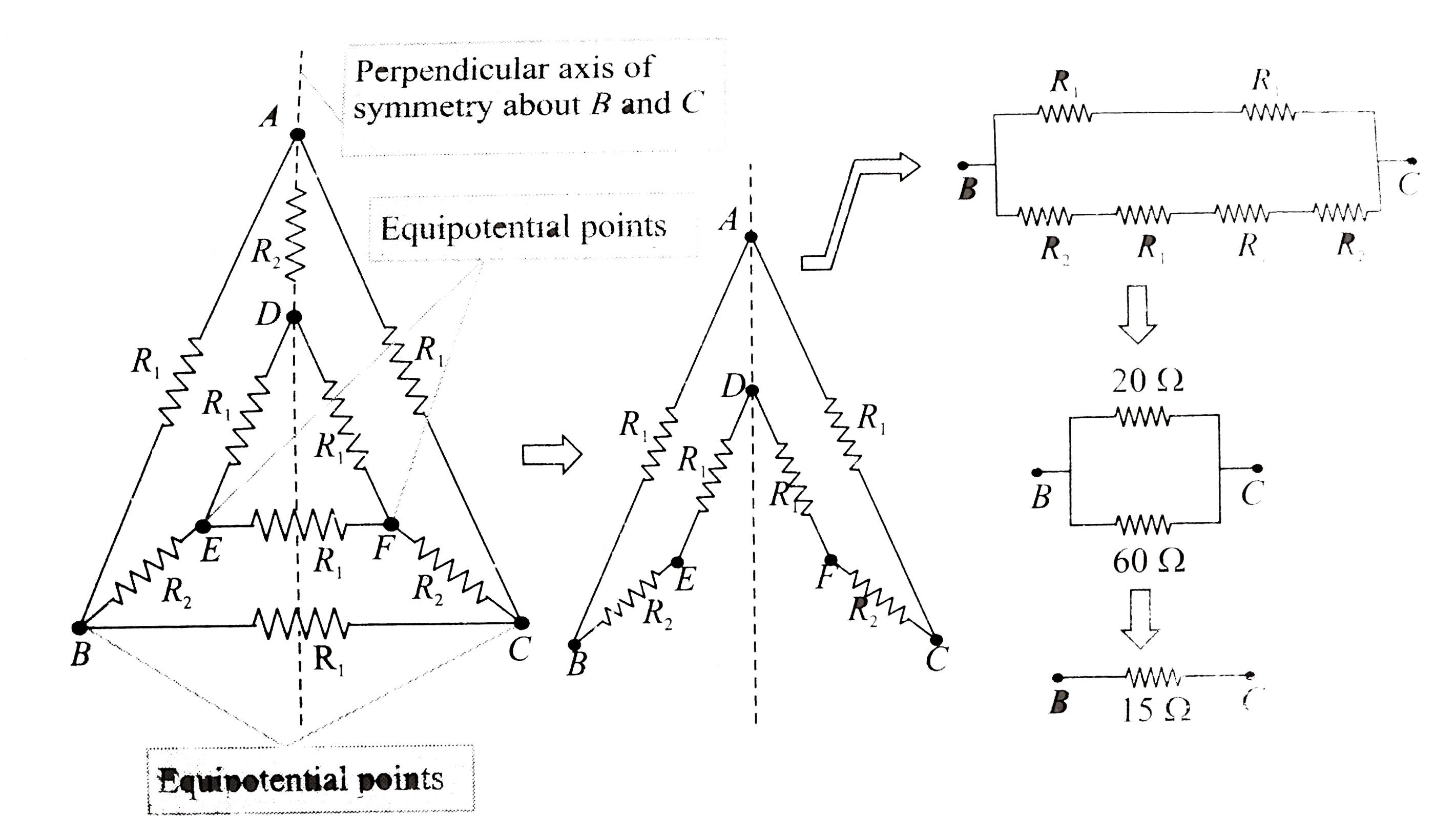
ii. Calculation of equivalent resistnace between B and C :
There exists perpendicular axis of symmetry about line x-y
Hence, the points symmetrical about x-y are equipotential,
i.e., points (E and F) and (B and C) are equipotential. Thus,
the resistance connected across these points can be removed. Also points A and D are lying on the perpendicular axis of symmetry. Hence, points A and D are also equipotential. The
resistances conneted between A and D can also be removed.
The circuit reduces as shown, and the steps - by step procedure
is given in fig. 5.56
|
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Knowledge Check
In the given figure, R=3Ω. Determine equivalent
resistance between points A and B.
 . A3ΩB2ΩC15ΩD6Ω
. A3ΩB2ΩC15ΩD6ΩEquivalent resistance between the points A and B (in Ω)
 .A15B114C213D312
.A15B114C213D312Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
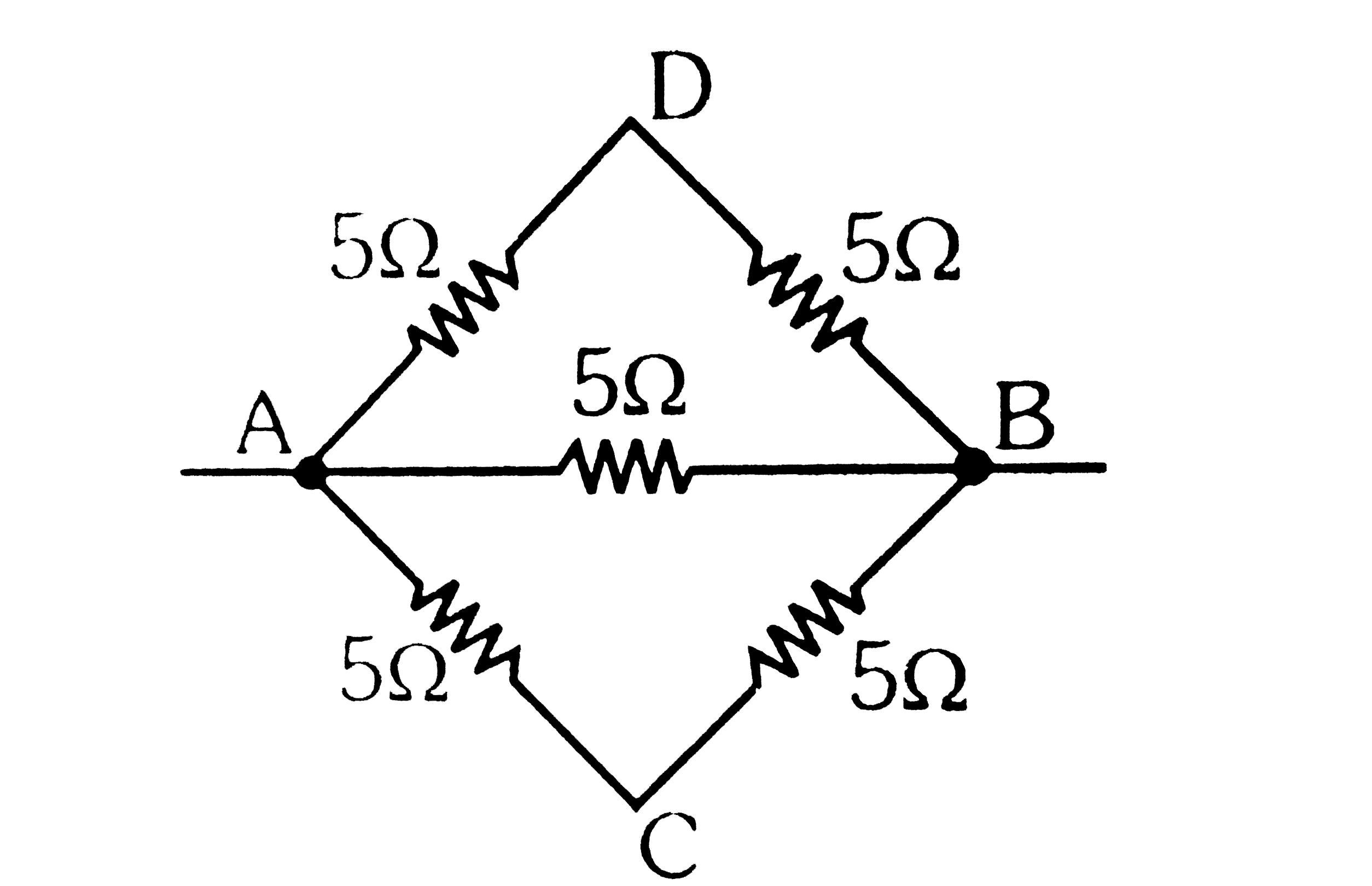 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
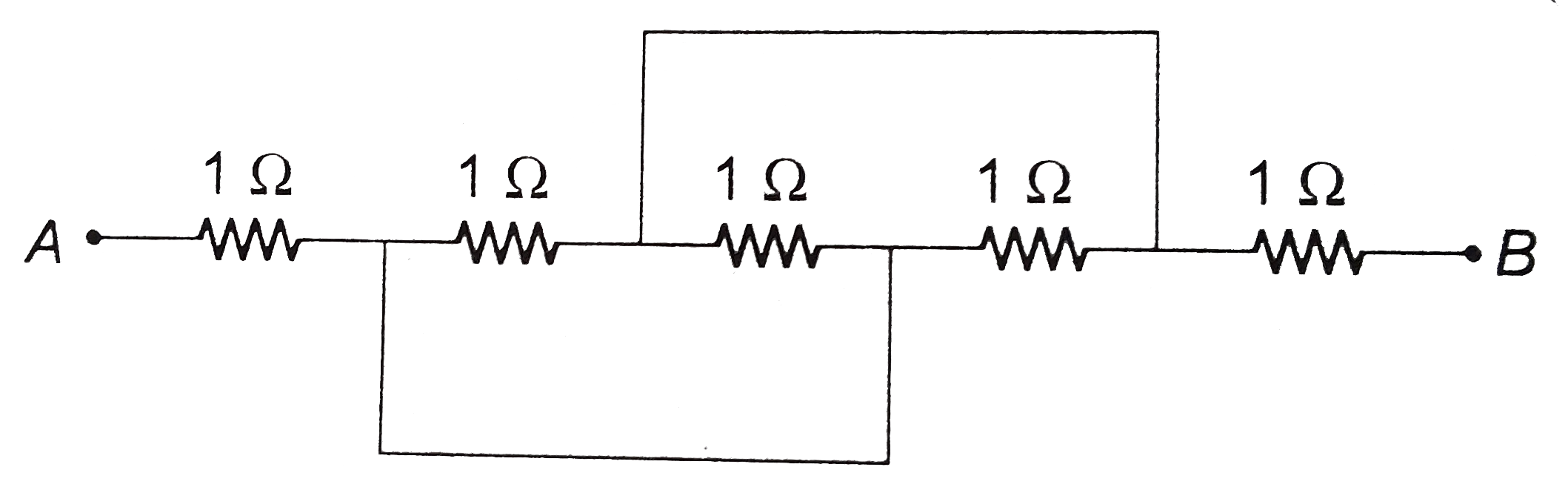
If the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
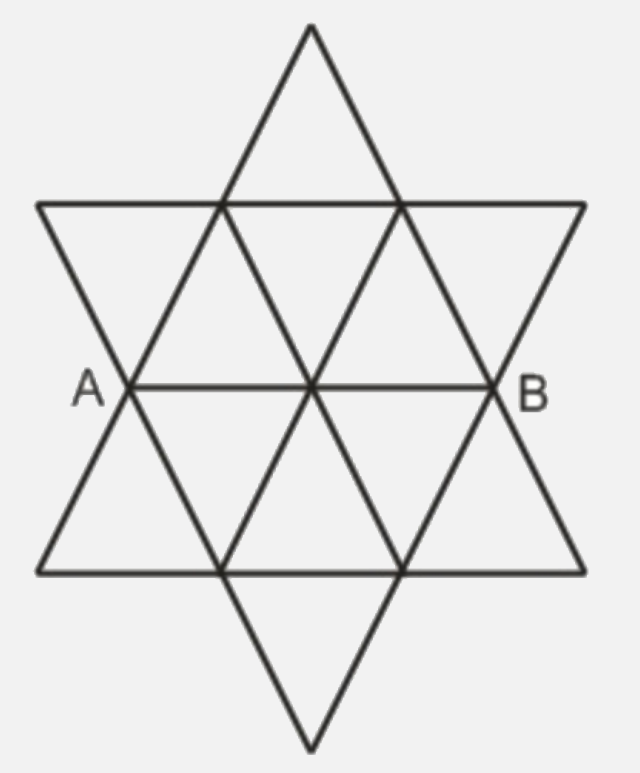
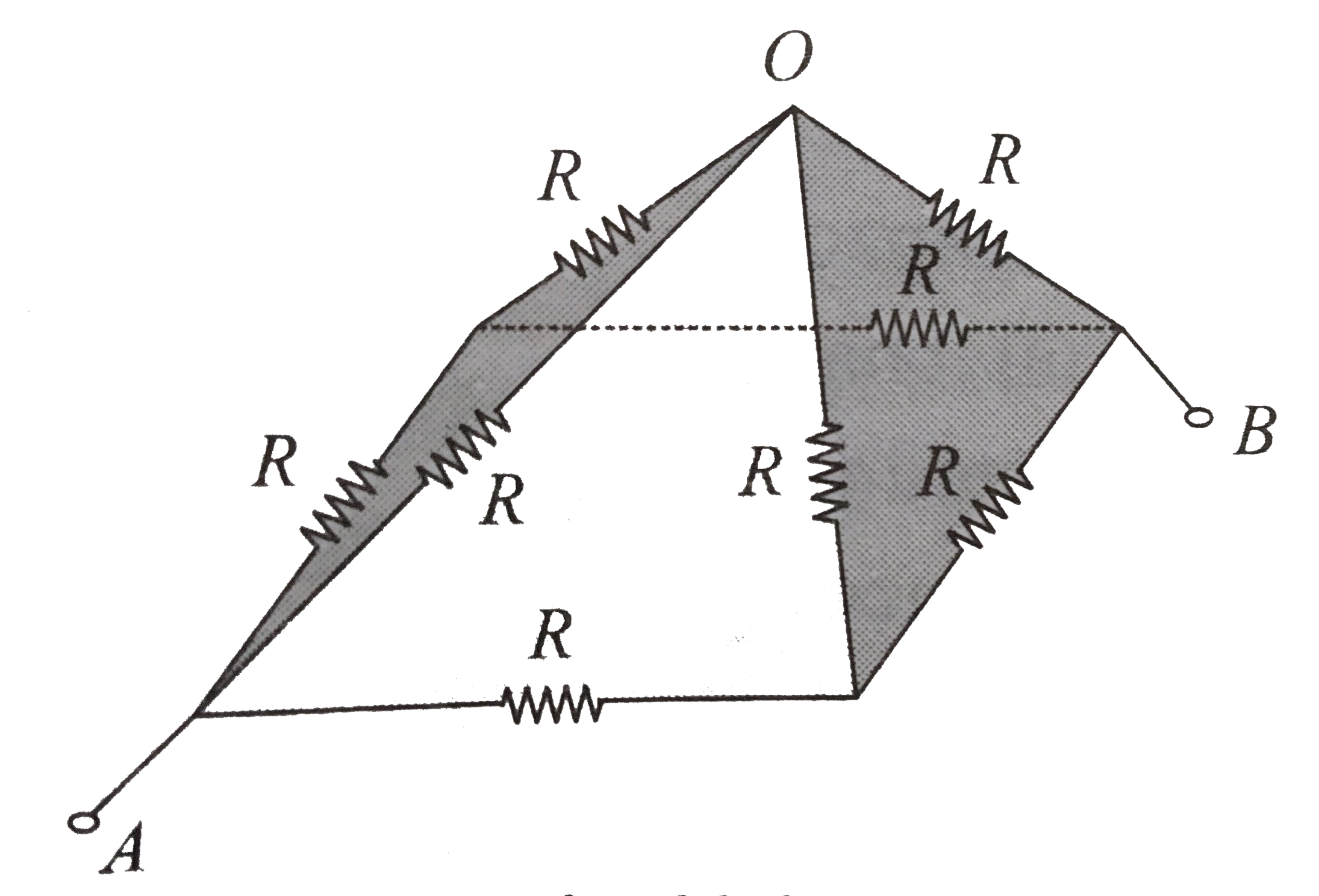
View SolutionThree equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is
View SolutionThe equivalent resistance between points A and B in the network shown in fig. is –
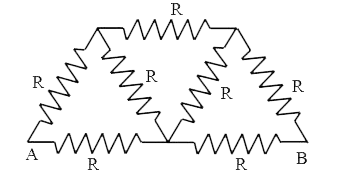
View SolutionFor the circuit shown in fig. the equivalent resistance between A and C is

View SolutionThe equivalent resistance between the points A and B in A the circuit shown in Fig. is
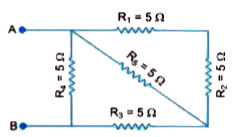
View Solution