Consider
<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V03_C04_E01_141_Q01.pngwh=80%mx-autosty≤=background:white;>.<br>Thechar≥appear∈gisC_(2) is.
E(C3C4C1+C2)
E(C1C2C1+C2)
E(C1C2C3+C4)
E(C3C4C3+C4)
The correct Answer is:B
Let charge be as shown. (Capacitors in series have the same the charge.)
Taking loop containing C1,C2, and E, we get
qC1+qC2−E=0 or q=E[C1C2C1+C2]
Similarly, from loop containing C3,C4, and E, we get
q'C3+q'C4−E=0 or q'=E[C3C4C3+C4]
Now, VA−VB=qC2−q'C
=E[C1C1+C2−C3C3+C4]
=E[C1C4−C3C2(C1+C2)(C3+C4)]
Now VA−VB=E⇒C1C4−C2C3=0
or C1C2=C3V4.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Multile Correct
11 Videos
- ATOMSBOOK - CENGAGE PHYSICSCHAPTER - ATOMSEXERCISE - QUESTION BANK
40 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
The charges appearing on inner surfaces of a parallel plate capacitor are q_( i and )q_(2) . The charges appearing on outer surfaces of the capacitor are equal.Find the potential difference between plates of the capacitor if capacitances is C.
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View Solution
Knowledge Check
Condsider
 .
.
Now the switch is shifted to position 2. The charge appearing on capacitor C3 isA225μCB235μCC270μCD75μCFor the system shown in capacitance is C The left plate is given a charge Q1 and the is closed.
 .
.
Find the charge appearing on the inner face of the left plate.ACV−Q12BCV+Q1CCV+Q12DCVThe circuit is in a steady state.
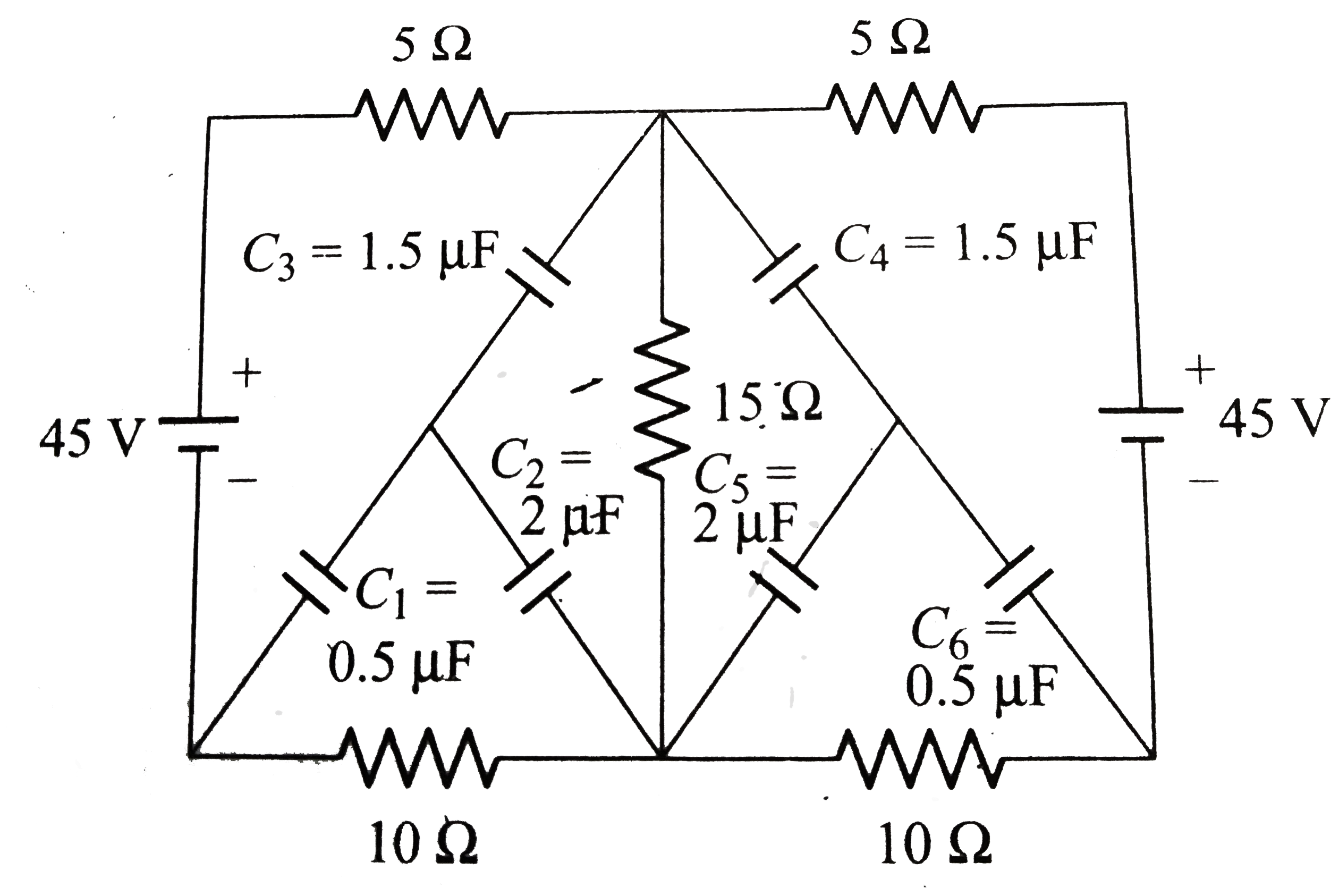
The charge in capacitor C2 isA30μCB10μCC20μCD40μC
Figure shows three concentric thin spherical shells A, B and C of radii a, b and c respectively. The shells A and C are given charges q and -q respectively and the shell B is earthed. Find the charges appearing on the surfaces of B and C.

View SolutionThere are three concentric metallic spherical shells of radius a, b and c respectively as shown in the figure. The innermost sphere is given a charge q and the outermost sphere is given a charge 4q while the middle sphere is earthed. Find the charges appearing on the inner and outer surfaces of middle sphere.
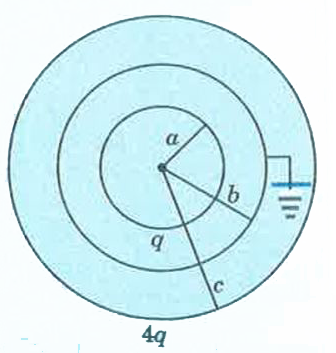
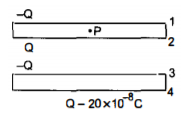
View SolutionThe negative plate of a parallel plate capacitor is given a charge of −20X10−8C. Find the charges appearing on the four surface of the capacitor plates.
View SolutionConsider the situation shown in the figure. The capacitor A has a charge q on it whereas B is uncharged. The charge appearing on the capacitor B a long 7 time after the switch is closed is :
 .
.
View SolutionThere are three concentric metallic spherical shells of radii R, 2R and 3q, respectively. The middle spherical shell is connected to earth. Let q1 be the charge appearing on the inner surface of the middle sphere and q2 be the charge on outer surface of the middle sphere. Similarly q3 is the charge appearing on inner surface of outermost sphere and q4 is the charge appearing on outer surface of outermost sphere.

View Solution
