The point charges −2q,−2q and +q are put on the vertices of an equilateral triangle of side a. Find the work done by some external force in increasing the separation to 2a (in joules).
The correct Answer is:0
To solve the problem of finding the work done by an external force in increasing the separation of the point charges from a to 2a, we will follow these steps:
Step 1: Understand the Initial Configuration
We have three point charges placed at the vertices of an equilateral triangle:
- Charge at vertex A: −2q
- Charge at vertex B: −2q
- Charge at vertex C: +q
The side of the triangle is a.
Step 2: Calculate the Initial Potential Energy (Ui)
The potential energy between two point charges Q1 and Q2 separated by a distance r is given by the formula:
U=kQ1Q2r
where k is Coulomb's constant.
We will calculate the potential energy for each pair of charges:
1. UAB between charges at A and B:
UAB=k(−2q)(−2q)a=k4q2a
2. UBC between charges at B and C:
UBC=k(−2q)(+q)a=−k2q2a
3. UCA between charges at C and A:
UCA=k(+q)(−2q)a=−k2q2a
Now, sum these energies to find the total initial potential energy Ui:
Ui=UAB+UBC+UCA=k4q2a−k2q2a−k2q2a=k4q2a−k4q2a=0
Step 3: Calculate the Final Potential Energy (Uf)
When the charges are moved to a separation of 2a, we repeat the calculation for the new distances:
1. UAB between charges at A and B:
UAB=k(−2q)(−2q)2a=k4q22a=k2q2a
2. UBC between charges at B and C:
UBC=k(−2q)(+q)2a=−k2q22a=−kq2a
3. UCA between charges at C and A:
UCA=k(+q)(−2q)2a=−k2q22a=−kq2a
Now, sum these energies to find the total final potential energy Uf:
Uf=UAB+UBC+UCA=k2q2a−kq2a−kq2a=k2q2a−k2q2a=0
Step 4: Calculate the Work Done
The work done W by the external force in moving the charges is given by the change in potential energy:
W=Uf−Ui=0−0=0 joules
Conclusion
The work done by the external force in increasing the separation of the charges from a to 2a is 0 joules.
---
We have three point charges placed at the vertices of an equilateral triangle:
- Charge at vertex A: −2q
- Charge at vertex B: −2q
- Charge at vertex C: +q
The potential energy between two point charges Q1 and Q2 separated by a distance r is given by the formula:
U=kQ1Q2r
where k is Coulomb's constant.
1. UAB between charges at A and B:
UAB=k(−2q)(−2q)a=k4q2a
2. UBC between charges at B and C:
UBC=k(−2q)(+q)a=−k2q2a
3. UCA between charges at C and A:
UCA=k(+q)(−2q)a=−k2q2a
Ui=UAB+UBC+UCA=k4q2a−k2q2a−k2q2a=k4q2a−k4q2a=0
When the charges are moved to a separation of 2a, we repeat the calculation for the new distances:
1. UAB between charges at A and B:
UAB=k(−2q)(−2q)2a=k4q22a=k2q2a
2. UBC between charges at B and C:
UBC=k(−2q)(+q)2a=−k2q22a=−kq2a
3. UCA between charges at C and A:
UCA=k(+q)(−2q)2a=−k2q22a=−kq2a
Uf=UAB+UBC+UCA=k2q2a−kq2a−kq2a=k2q2a−k2q2a=0
The work done W by the external force in moving the charges is given by the change in potential energy:
W=Uf−Ui=0−0=0 joules
The work done by the external force in increasing the separation of the charges from a to 2a is 0 joules.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.1
Explore 14 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.2
Explore 15 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Comprehension
Explore 31 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View Solution
Knowledge Check
Three point charges 1C, -2C and -2C are placed at the vertices of an equilateral triangle of side length one meter. The work done by an external force to increase the separation of the charges to 2 meters in joules is: (∈0 is permittivity of air)
A14π∈0B18π∈0C116π∈0D0Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three point charges q, q & - 2q placed, at the corners of equilateral triangle of side 'L ' Calculate work done by external force in moving all the charges far apart without acceleration
A14πε03q2LB−14πε03q2LC14πε05q2LD−14πε05q2L
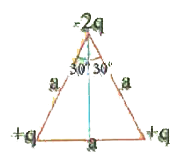
Three points charges =q, -2q, +q are arranged on the vertices of an equilaterial triangle as shown in the figure. Find he dipole moment of the system.
View SolutionThree equal charges Q are at the vertices of an equilateral triangle of side A. How much work is done (by an external agent) in bringing them closer to an equilateral triangle of side A/2?
View SolutionThree equal charge Q are at the vertices of an equilateral triangle of side A. How much work is done (by an external angent ) in bringing them closser to an equilateral triangle of side A/2?
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View Solution

