Three charges $q_{1} = 1 μ C, q_{2} = 2 μ C$ and $q_{3} = 3 μ C$ are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge $q_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

Method I. In the figure
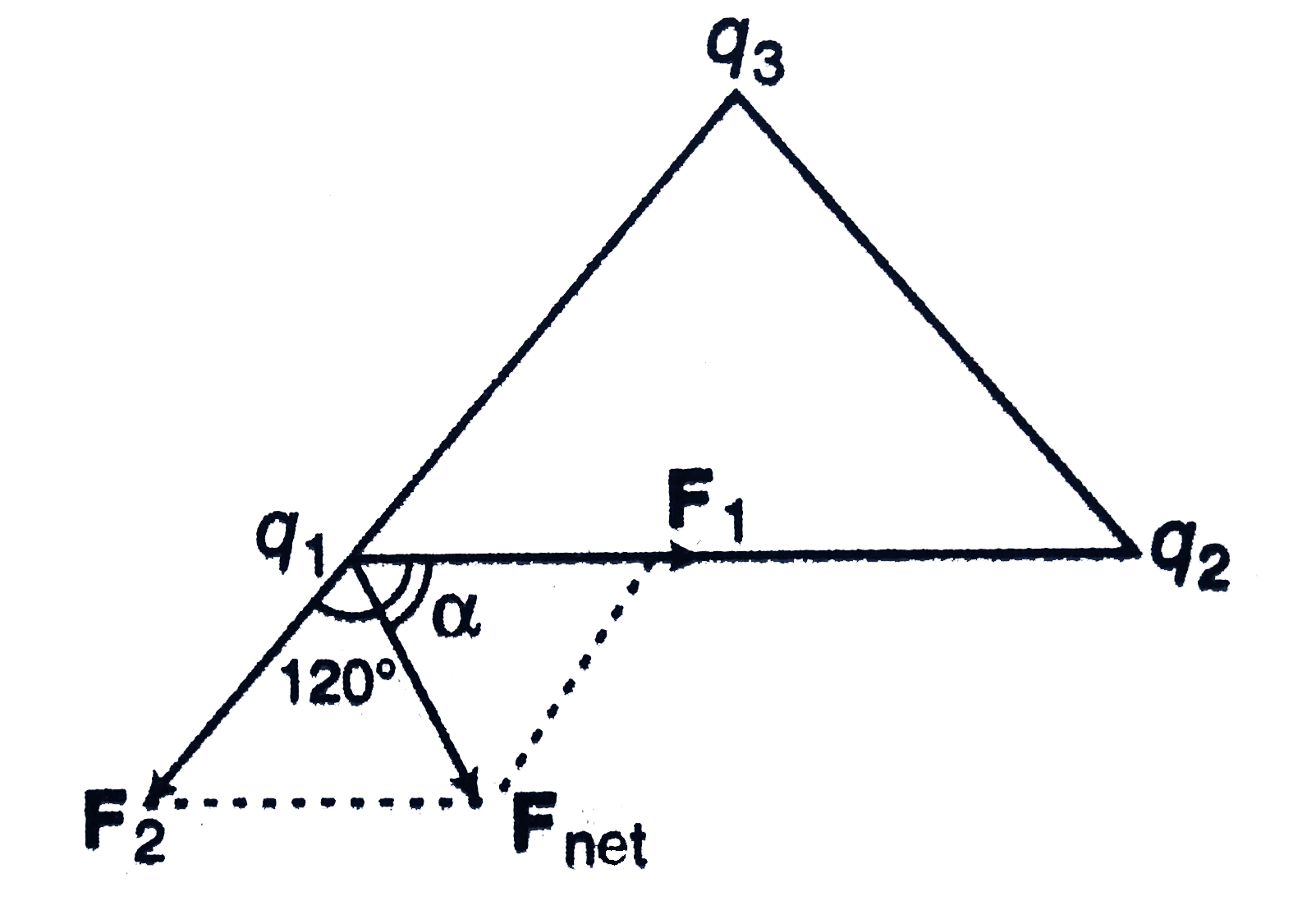$< b r >$ |F_(1)|=F_(1)=1/(4piepsilon_0).(q_1q_2)/r^2 $< b r > = m a g n i t u d e o f f or c e b e t w e e n$ q_1 and q_2 $< b r >$ ((9.0xx10^9)(1.0xx10^-6)(2.0xx10^-6))/((1.0)^2) $< b r >$ =1.8xx10^-2N $< b r >$ Similarly $| F_{2} | = F_{2} = \frac{1}{4 π ε_{0}} . \frac{q_{1} q_{3}}{r^{2}}$
$= m a g n i t u d e o f f or c e b e t w e e n$ q_1 $and$ q_3 $< b r >$ =((9.0xx10^9)(1.0xx10^-6)(3.0xx10^-6))/((1.0)^2) $< b r >$ =2.7xx10^-2N $< b r > N o w,$ |F_"net")|=sqrt(F_1^2+F_2^2+2F_1F_2cos120^@) $< b r >$ =(sqrt((1.8)^2+(2.7)^2=2(1.8)(2.7)(-1/2)))xx10^-2N $< b r >$ =2.38xx10^-2N $< b r > and$ tan alpha=(F_2sin120^@)/(F_1+F_2cos120^@) $< b r >$ =((2.7xx10^-2)(0.87))/((1.8xx10^-2)+(2.7xx10^-2)(-1/2)) $< b r > or$ alpha=79.2^@ $< b r > T h u s, t h e \neq t f or c e o n c h a r \geq$ q_1 $i s$ 2.38xx10^-2 $N a t a n ∠$ alpha=79.2^@ $w i t h a l \in e j o \in \in g$ q_1 $and$ q_2 $a s s h o w n \in t h e f i g u r e . < b r > M e t h o d 2 . I n t h i s f i g u r e m e t h o d \leq t u s a s \sum e a c \infty r d \in a t e a x e s w i t h$ q_1 $a t or i g \in a s s h o w n \in f i g u r e . T h e c \infty r d \in a t e o f$ q_1,q_2 $and$ q_3 $\in t h i s c \infty r d \in a t e s y s t e m a r e$ (0,0,0), (1m,0,0) $and$ (0.5m, 0.87m,0) $r e s p e c t i v e l y . N o w < b r > < i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_VOL_4_C24_S01_008_S02.png w h = 80% mx-auto s t y \leq = background:white; >$
$F_{1}$ =force of $q_{1}$ due to charge $q_{2}$
$= \frac{1}{4 π ε_{0}} . \frac{q_{1} q_{2}}{{| r_{1} - r_{2} |}_{1}^{3}} (r_{1} - r_{2})$
$= \frac{(9.0 \times 10^{9}) (1.0 \times 10^{- 6}) (- 2.0 \times 10^{- 6})}{{(1.0)}^{3}} [(0.1) ˆ i + (0 - 0) ˆ j + (0 - 0) ˆ k]$
$= (1.8 \times 10^{- 2} ˆ i) N$
and $F_{2}$ =Force on $q_{1}$ due to charge $q_{3}$
$= \frac{1}{4 π ε_{0}} . \frac{q_{1} q_{3}}{{| r_{1} - r_{3} |}_{1}^{3}} (r_{1} - r_{3})$
$= \frac{(9.0 \times 10^{9}) (1.0 \times 10^{- 6}) (3.0 \times 10^{- 6})}{{(1.0)}^{3}} [(0 - 0.5) ˆ i + (0 - 0 - 0.87) ˆ j + (0 - 0) ˆ k]$
$= (- 1.35 ˆ i - 2.349 ˆ j) \times 10^{- 2} N$
Therefore net force on $q_{1}$ is $F = F_{1} + F_{2}$
$= (0.45 ˆ i - 2.349 ˆ j) \times 10^{- 2} N$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Three charges $4 μ C, 4 μ C and - 4 μ C$ are placed at vertices of an equilateral triangle of side length 20cm. The potential centre is nearly.
A $3.1 \times 10^{3} V$
B $3.1 \times 10^{4} V$
C $3.1 \times 10^{5} V$
D $3.1 \times 10^{6} V$
Four charges $q_{1} = 1 μ C, q_{2} = 2 μ C, q_{3} = - 3 μ C$ and $q_{4} = 4 μ C$ are kept on the vertices of a square of side $1 m$ . Find the electric potential energy of this system of charges.

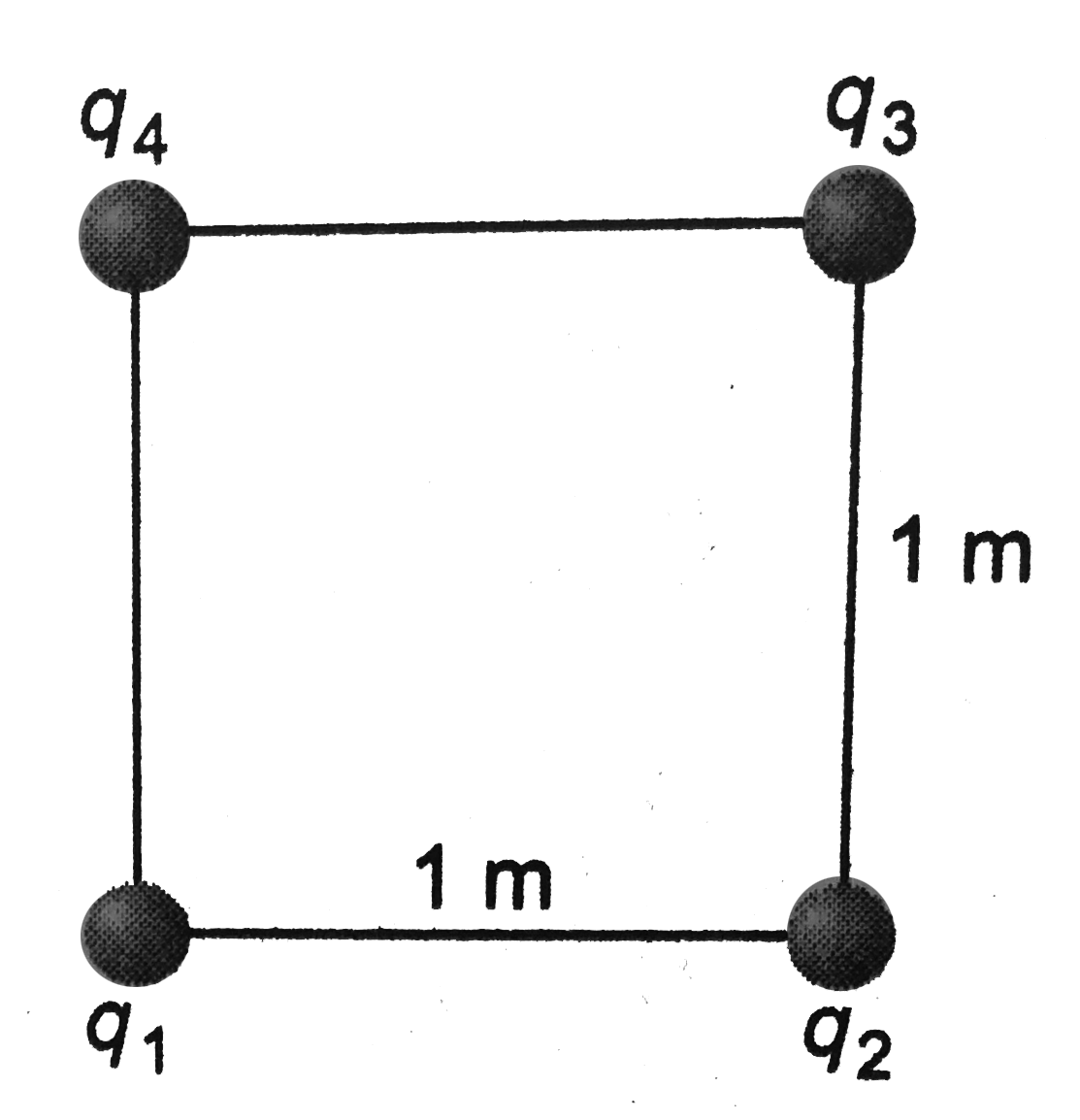A $- 5.28 \times 10^{- 2} J$
B $- 7.62 \times 10^{- 2} J$
C $- 8.91 \times 10^{- 2} J$
D $- 4.33 \times 10^{- 2} J$
Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A $(\frac{\sqrt{3}}{4 π ε_{0}}) {(\frac{q}{a})}^{2}$
B $(\frac{\sqrt{2}}{4 π ε_{0}}) {(\frac{q}{a})}^{2}$
C $(\frac{\sqrt{3}}{4 π ε_{0}}) {(\frac{q}{2 a})}^{2}$
D $(\frac{\sqrt{2}}{4 π ε_{0}}) {(\frac{2 q}{a})}^{2}$

DC PANDEY-ELECTROSTATICS-Medical entrances gallery

Home
Ask Doubt
Profile