A small conducting sphere of radius a, carrying a charge +Q, is placed inside an equal and oppositely charged conducting shell of radius b such that their centers coincide. Determine the potential at a point which is at a distance c from center such that a<c<b.
k(Q/c+Q/b)
k(Q/a+Q/b)
k(Q/a−Q/b)
k(Q/c−Q/b)
The correct Answer is:d
V=kQc−kQb

Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A conducting sphere of radius 2R carrying charge Q is joined to an uncharged conducting sphere of radius R. Find the charge flow through cinnecting wire.
View SolutionInside a charged thin conducting shell of radius R, a point charge +Q is placed as shown in figure potential of shell may be
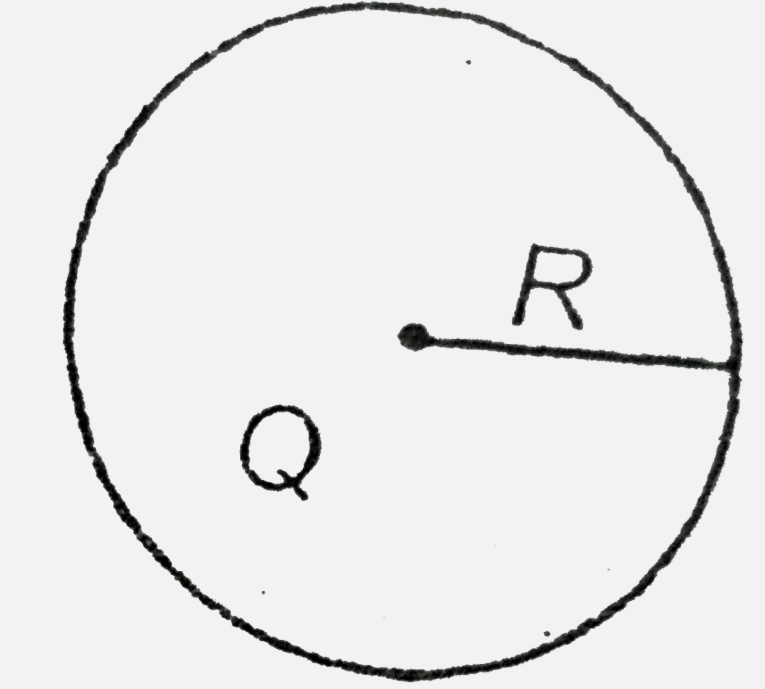
View Solution
Knowledge Check
A conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
AQ/3 amount of charge will flow from the sphere to the shellB20/3 amount of charge will flow from the sphere to the shellCQ amount of charge will flow from the sphere to the shellDkQ24R amount of heat will be producedA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
AQ/4BQ/3CQ/2D2Q/3A conducting sphere A of radius a ,with charge Q , is placed concentrically inside a conducting shell B of radius b . B is earthed. C is the common centre of the A and B
AThe field at a distance r from C , where a≤r≤b , is kQr2BThe potential difference between A and B is kQ(1b−1b)CThe potential at a distance r from C, where a≤r≤b, is kQ(1r−1b)DAll options are correct
A charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View SolutionCalculate amount of charge flow, when a conducting sphere of radius R and carrying a charge Q, is joined to an uncharged conducting sphere of radius 2R.
View SolutionA conducting sphere A of radius a, with charge Q is placed concentrically inside a conducting shell B of radius b. B is earthed, C is the common centre of A and B. If P is the point between shells A and B at distance r from center C then Match the proper entries from column-2 to column-1 using the codes given below the columns,
(use a=1m,b=3m,r=2m and K=14πεo)
View SolutionA conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common center of AandB. Study the following statements.
(i) The potential at a distance r from C, where
a≤r≤b,is14πε0(qr)
(ii) The potential difference between AandB is
14πε0Q(1r−1B)
(iii) The potential at a distance r from C, where
a≤r≤b,is14πε0Q(1r−1B)
Which of the above statements are correct ?
 .
.
View SolutionA point charge +Q is placed at point B at a distance 2R from the center O of an uncharged thin conducting shell of radius R as shown in figure. If VA be the potential at point A, which is at a radial distance of R/2 from the center of the shell, then
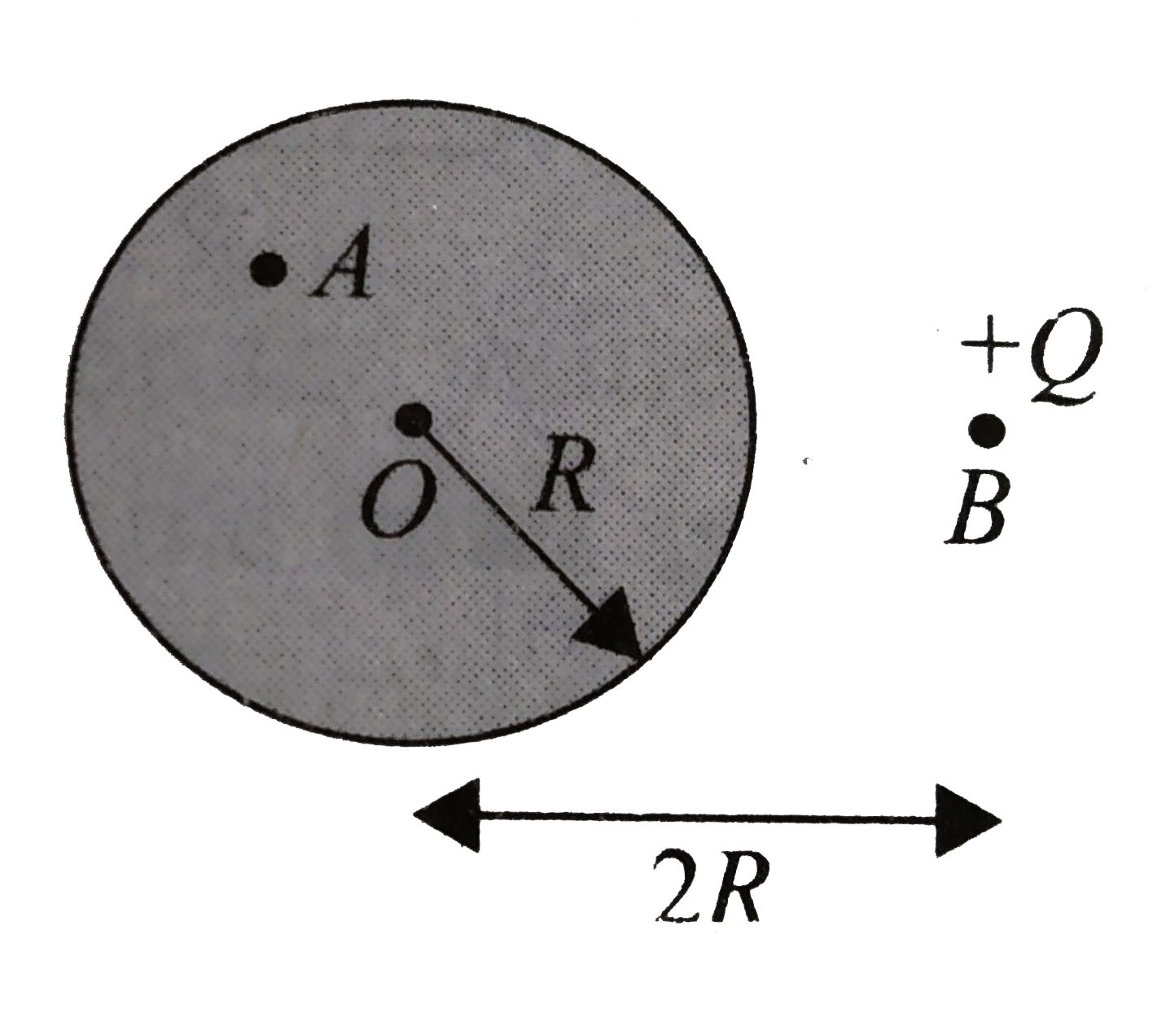
View Solution
