Water from a tap, maintained at a costant potential V, is allolwed to fall by drops of radius r through a small hole into a hollow conducting sphere of radius R standing on an insulating stand until it fills the entire sphere. Find the potential of the hollow conductor after it is completely filled with water.
The correct Answer is:
Potential of a drop
or
Therefore, total charge
(n = total number of drops)
Also,
Hence, potential of the hollow conductor
=
=.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Single Correct
Explore 56 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Multiple Correct
Explore 10 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:Exercise 3.3
Explore 9 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICSChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
The centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View Solution
Knowledge Check
Acidified water from certain reservoir kept at a potential V falls in the form of small droplets each of radius r through a hole into a hollow conducting sphere of radius a. The sphere is insulated and is initially at zero potential. If the drops continue to fall untill the sphere is half full, the potential acquired by the sphere is
Aa2V2r2B√arV2Ca3V2r3DaVrThe potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0RA non conducting sphere of radius R is charged uniformly. At what distance from its surface is the electrostatic potential is half the potential at its centre ?
ARBR/2CR/3D2R
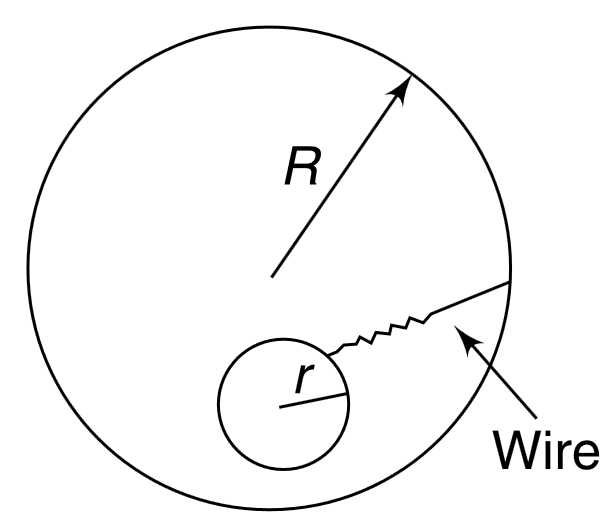
A conducting ball of radius r is charged to a potential V0. It is enveloped by a thin walled conducting sphere of radius R (gt r) and the two spheres are connected by a conducting wire. Find the potential of the outer sphere.
View SolutionA hollow conducting sphere of radius R has a charge (+Q) on its surface. What is the electric potential within the
sphere at a distance r=R3 from its centre ?
View SolutionA large hollow metal sphere of radius R has a small opening at the top. Small drops of mercury each of radius r and charged to a potential V fall into the sphere. The potential of the sphere becomes V' after N drops fall into it . Then,
View SolutionA hollow spherical conductor of radius r potential of 100 V at its outer surface. The potential inside the hollow at a distance ofr2 from its centre is
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View Solution

