A nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
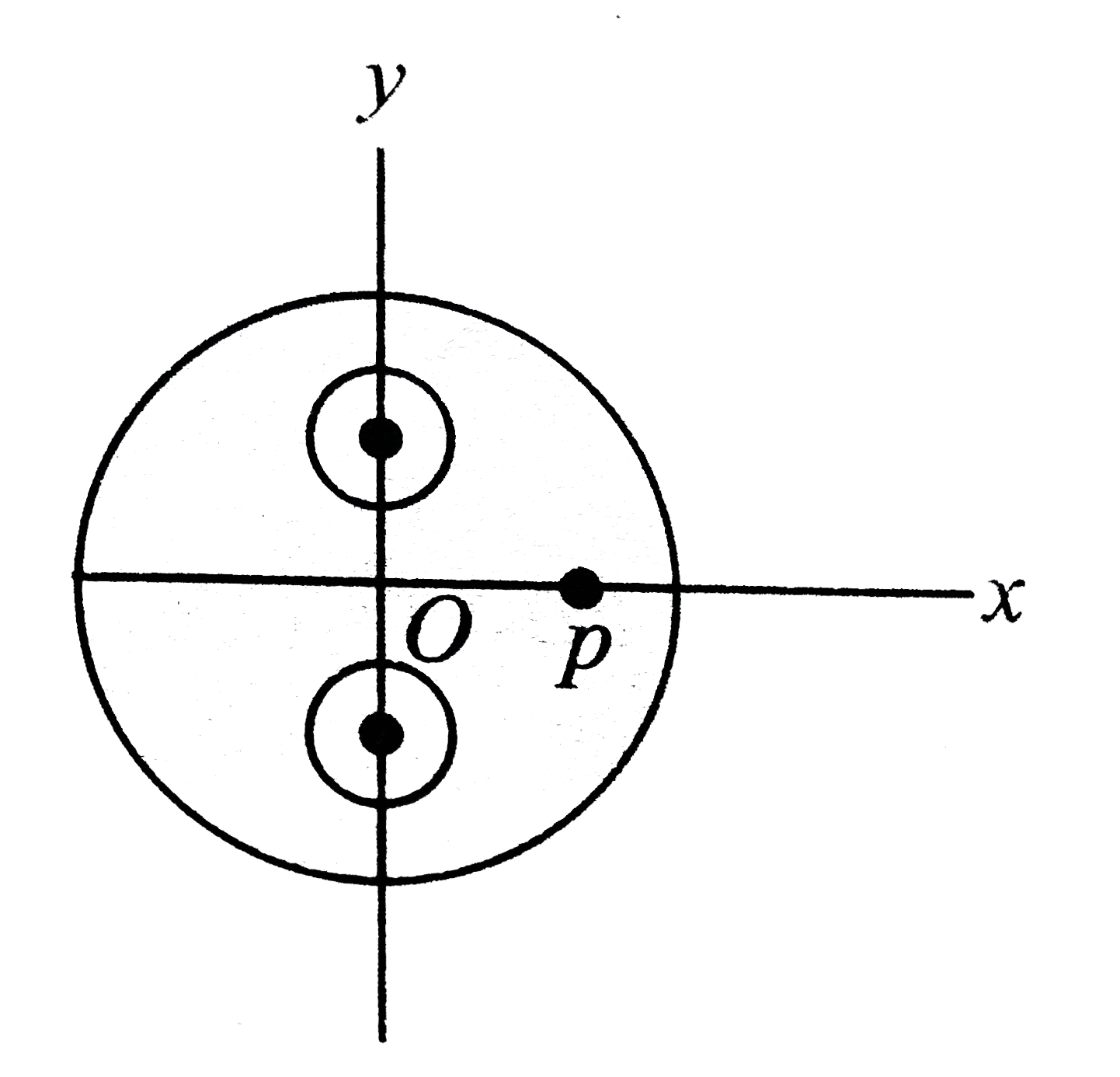A nonconducting sphere of radius R = 5 cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r = 1 cm, whose centers are at 0,3 cm and 0,-3 cm, respectively, and solid material of the sphere has uniform positive charge density rho = 1 // pi mu Cm^-3. Calculate the electric potential at point P (4 cm, 0). ..

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:4345πε0×10−10 Volt

Charge on the sphere (including cavities)
Q=43πR3ρ=43π(5×10−2)31π×10−6=5003×10−12C
Charge in a volume equal to that of cavity
q=43πR3ρ=43π(1×10−2)31π×10−6=43×10−12C
Potential at P
Vp=Vwhole sphere−2Vcavity
=kQ2R[3−x2R2]−2kq5×10−2
=9×109×(500/3)×10−122×5×10−2[3−(45)2]
−2×9×109×(4/3)×10−125×10−2
=87325=34.92V.

Updated on:21/07/2023
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
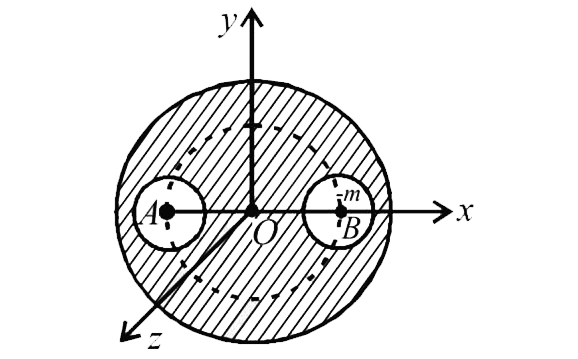    ocr_image

    AThe gravitational force due to this object at the origin is zero.
    Bthe gravitational force at the point B(2,0,0) is zero.
    Cthe gravitational potential is the same at all points of circle y2+z2=36
    Dthe gravitational potential is the same at all points on the circle y2+z2=4.

  • A sphere of radius 1 cm has potential of 10000V, then energy density near its surface will be

    A64×105J/m3
    B8×103J/m3
    C32J/m3
    D4.425J/m3

  • A sphere of radius 1cm has potential of 8000V, then energy density near its surface will be

    A64×105J/m3
    B8×103J/m3
    C32J/m3
    D2.83J/m3