Electrically charged drops of mercury fall from an altitude h into a spherical metal vessel of radius R. There is a small opening in the upper part of the vessel. The mass of each drop is m, and the charge on the drop is Q. What will be the number n of the last drop that can still enter the sphere?
Each charged drop that falls into the conducting vessel increases the charge of the vessel by Q. The accumulated charge on the conducting vessel is uniformly distributed on the surface of the vessel. The charged spherical vessel crates its own electric field that can be calculated by assuming the electric charge of the sphere to be concentrated at its center. Let n drops have accumulated in the vessel and (n + 1) th be in the state of equilibrium at a height h. The equilibrium exists under the influence of repulsive coulomb force (directed upward) and force of gravity (downward). Thus, we have
(nQ)Q4πε0(h−R)2=mg
Hence
n=4πε0mg(h−R)2Q2.
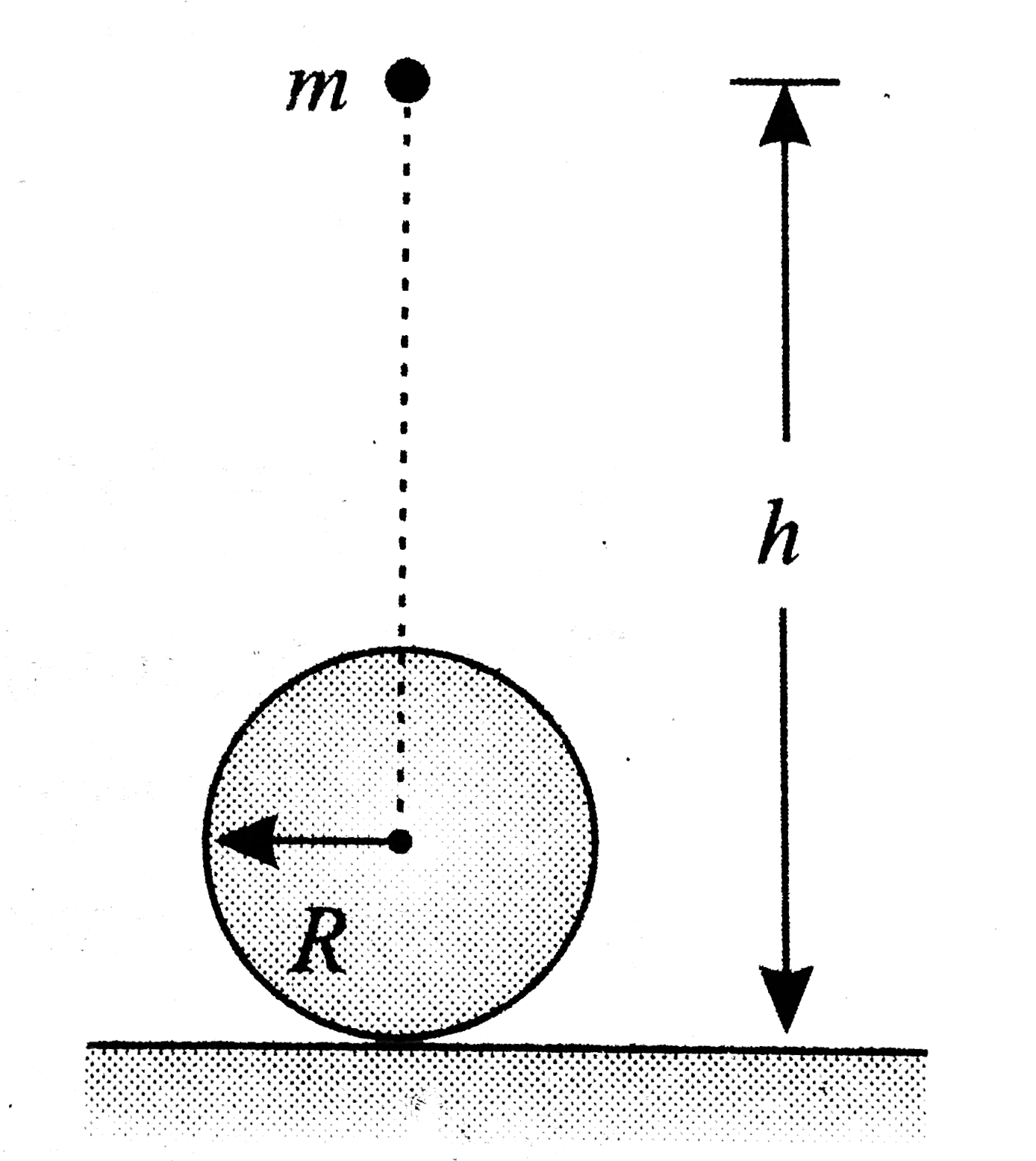 .
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Electrically charged drops of nercury fall from an altitude h into a sperical metal vessel of radius R. There is a small opening in the upperapart of the vessel. The mass of eanc drop is m, and the charge on the drop is Q. What will be the number n of the last drop taht can still enter the sphere?
View SolutionThousand small mercury drops each of the radius r and charge q coalesce together to form one spherical drop. What is the ratio of the potential of the bigger drop to that of the smaller one?
View Solution
Knowledge Check
A large hollow metal sphere of radius R has a small opening at the top. Small drops of mercury, each of radius r and charged to a potential of the sphere becomes V' after N drops fall into it.Then
AV'=V for any value of NBV'=V for N=(Rr)2/3CV'=V for N=(Rr)1/3DV'=V for N=RrA large hollow metal sphere of radius R has a small opening at the top. Small drops of mercury each of radius r and charged to a potential V fall into the sphere. The potential of the sphere becomes V' after N drops fall into it . Then,
AV'<V for all NBV'=V for N=1CV'=V for N=R/rDV'=V for N=(R/r)1/3N drops of mercury of equal radii and possessing equal charges combine to form a big spherical drop. Then the capacitance of the bigger drop compared to each individual drop is
AN timesBN2/3 timesCN1/3 timesDN5/3 times
When a big drop of water is formed from n small drops of water, the energy oss is 3E, where, E is the energy of the bigger drop. If R is the radius of the bigger drop and r is the radius of the smaller drop then number of smaller drops (n) is?
View Solution64 small drops of mercury each of radius r and charge q coalesce to form a big drop. The ratio of the surface density of charge of each small drop withh that of big drop is
View Solutionn charged drops, each of radius r and charge q, coalesce to from a big drop of radius R and charge Q. If V is the electric potential and E is the electric field at the surface of a drop, then.
View Solutionn small drops of same size are charged to V volts each .If they coalesce to from a singh larg drop, then its potential will be -
View Solution1000 small water drops each of radius r and charge q coalesce together to form one spherical drop. The potential of the bigger drop is larger than that of the smaller one by a factor
View Solution