An insulating rod having linear charge density λ=40.0μCm−1 and linear mass density μ=0.100kgm−1 is released from rest in a uniform electric field E=100Vm−1 directed perpendicular to the rod.
(a) Determine the speed of the rod after it has travelled 2.00 m
(b) How does your answer to part (a) change if the electric field is not perpendicular to the rod ?
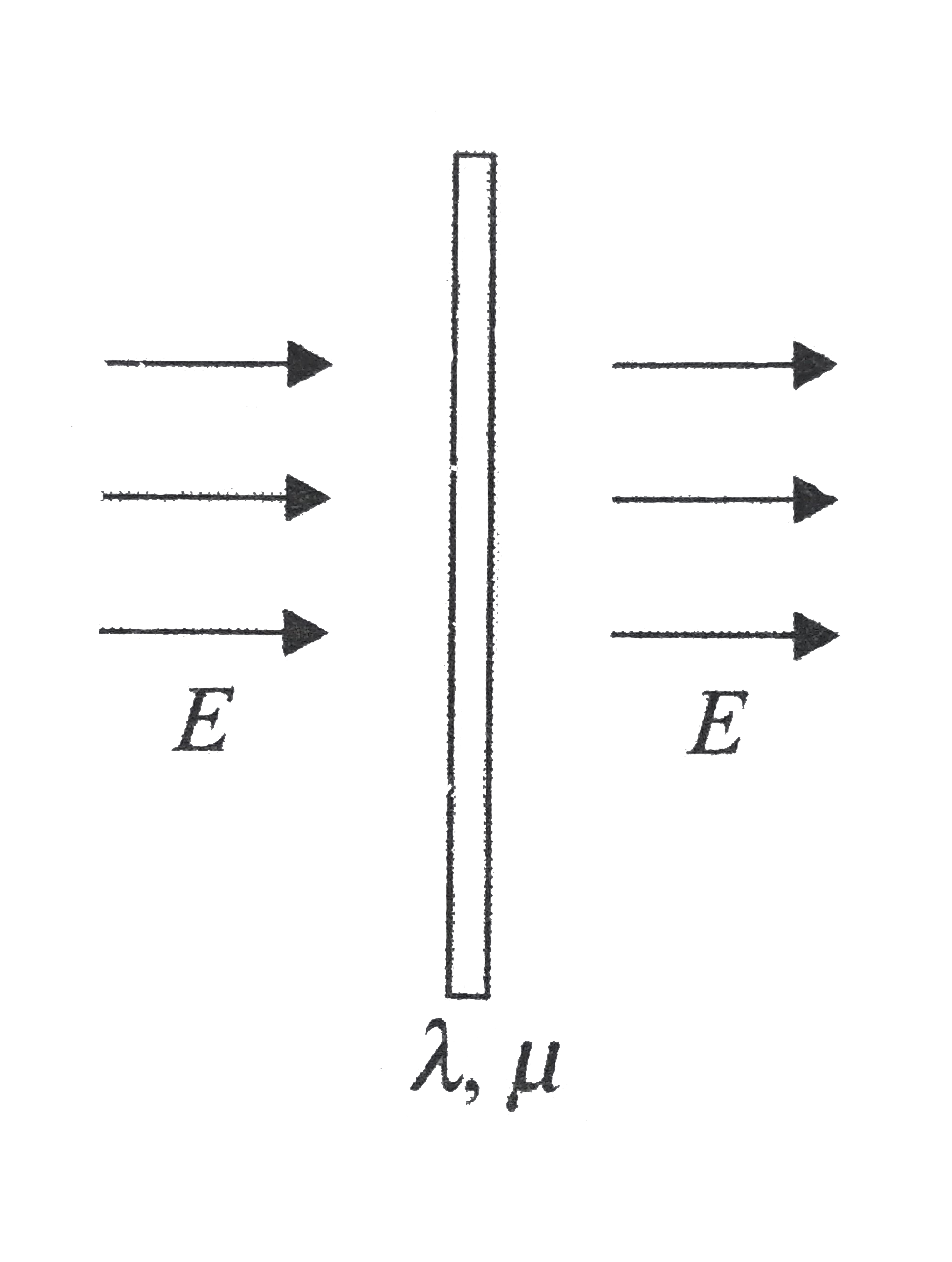
Arbitrarily take V=0 at the initial point. Then at distance d downfield, where L is the rod length,
V=−Ed and Ue=λLEd
a. (K+U)i=(K+U)f
or 0+0=12μLv2−λLEd
or v=√2λEdμ=0.400ms−1
b. The same.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
An insulating rod of uniform linear charge density A and uniform linear mass density μ lies on a smooth table whose surface is xy-plane. A uniform electric field E is switched on in the space:

View SolutionA semi-infinite insulating rod has linear charge density λ. The electric field atthe pointPshown in figure-1.418 is:

View Solution
Knowledge Check
A protons of mass m charge c is released form rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is
A√2demEB√2dmEeC√2dEmeD√2dEedmA charged particle of mass m and charge e is released from rest in an electric field E. If kinetic energy of particle after time t is Ek and linear momentum is p, then
Ap=EetBp=2eEtCEK=e2E2t22mDEK=e2E2t2mIf the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
A4×105NC−1B2×106NC−1C8×107NC−1D12×107NC−1
A protons of mass m charge 2 e is released from rest in a uniform electric field of strength E .The time taken by it to travel a distance d in the field is..
View SolutionElectric Field||E due to rods
View SolutionTwo charged particle having masses in the ratio 2:3 and charges in the ratio 1:2 are released from rest in a uniform electric field.After a time 1 minute their K.E.will be in the ratio of
View SolutionA charged particle of mass m and charge e is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is Ek and the linear momentum is p. We have
View SolutionA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View Solution
