Two identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.
Facing surfaces have equal and opposite charge (by Gauss's theorem). Let
the facing surfaces have charges x and -x
[surfaces (2) and (3), respectively].
Then the charge on surfaces (1) and (2)
should be (q1−x)andx, respectively (by
conservation of charge). Facing metallic
surfaces always have equal and opposite
charge. Hence, charge appearing on
surfaces (3) and (4) will be -x and (q2+x), respectively.
Let us consider a point P inside the left plate. The net
electric field at P should be zero.



The net electric field at P will be due to the resultant of
electric fields due to the charges appearing on all four surfaces.
Thus,
E1+E3=E2+E4
⇒(σ12ε0+σ32ε0=σ22ε0+σ42ε0
⇒q1−x+x=q2+x+xorx=q1−q22
Hence, charge appearing on different surfaces are as shown
in figure

Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
14 Videos
Similar Questions
Some isolated metal plates with large surface areas are kept parallel to each other and total charges on each plate are as shown. Find the charge appearing on the surfaces of plates.
(a)
View SolutionTwo large metal plates with surface charge densities +σ and −σ are separated from each other by a distance of d. Find the force per unit area acting between them.
View Solution
Knowledge Check
Two identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
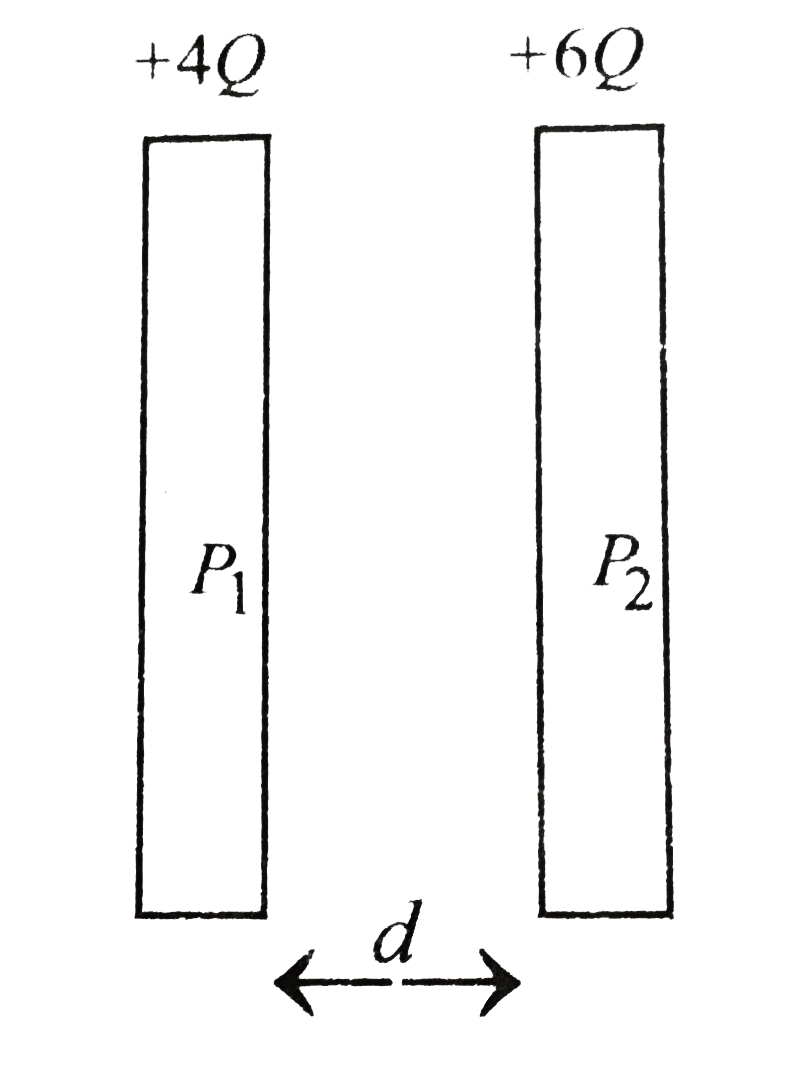 AVP1−VP2=QdAε0BVP1−VP2=−QdAε0CVP1−VP2=5QdAε0DVP1−VP2=−5QdAε0
AVP1−VP2=QdAε0BVP1−VP2=−QdAε0CVP1−VP2=5QdAε0DVP1−VP2=−5QdAε0Two identies conducting very large plates P1 and P2 having charges +4Q and +6Q are placed very closed to each other at separation d .The plate area of either face of the plate is A.the potential difference between plates P1 and P2 is
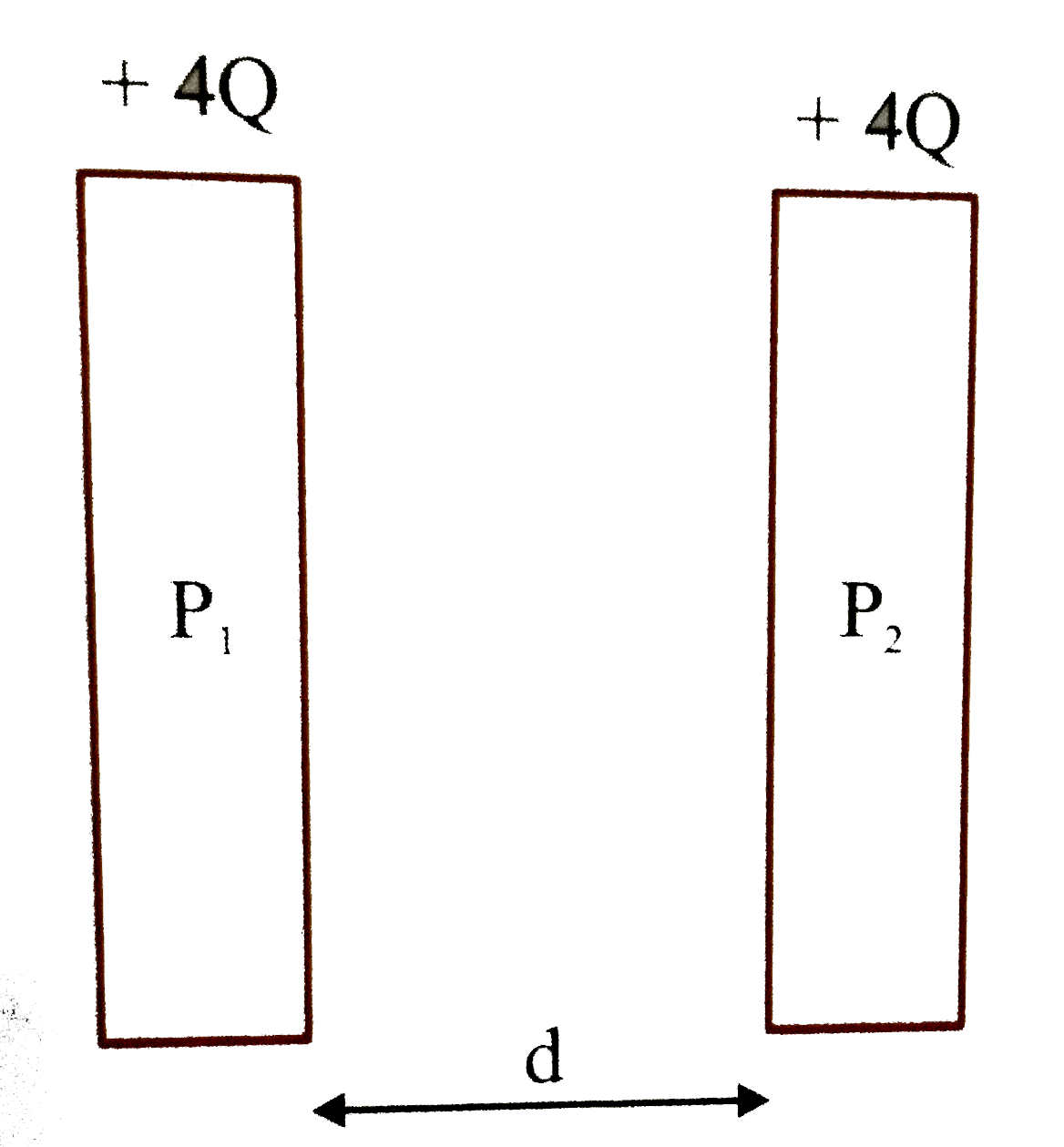 AVP1−VP2=QdAε0BVP1−VP2=−QdAε0CVP1−VP2=5QdAε0DVP1−VP2=−5QdAε0
AVP1−VP2=QdAε0BVP1−VP2=−QdAε0CVP1−VP2=5QdAε0DVP1−VP2=−5QdAε0Two conducting plates M and N, each having large surface area A (on one side), are placed parallel to each other in figure. The plate M is given charge Q1 and N, charge Q2(<Q1). Then
 Aelectric field at point A is (Q1−Q2)/2Aε0 toward right.Belectric field at point B is (Q1−Q2)/2Aε0 toward right.Celectric potential of N is greater than M.Dall of the above
Aelectric field at point A is (Q1−Q2)/2Aε0 toward right.Belectric field at point B is (Q1−Q2)/2Aε0 toward right.Celectric potential of N is greater than M.Dall of the above
Three large plates A, B and C are placed parallel to each other and charges are given as shown. The charge that appears on the left surface of plate B is
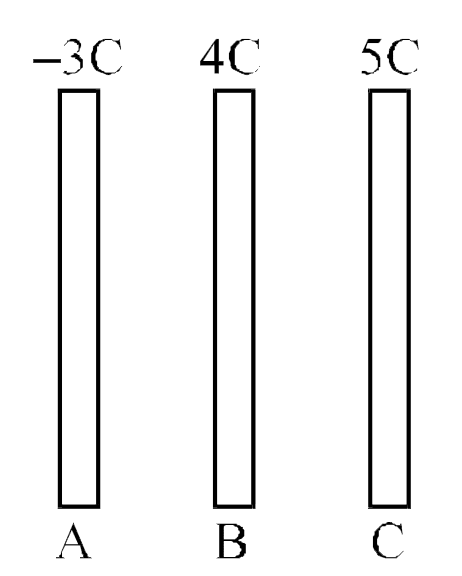
View SolutionTwo large metal plates each of area 1m2 are placed facing each other at a distance of 5 cm and carry equal and opposite charges on their faces. If the electric filed between the plates is 1000NC−1, find the charge on each plate.
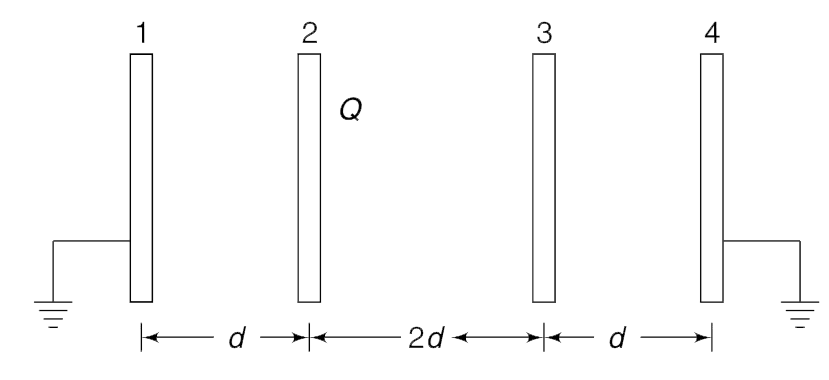
View SolutionFour large identical metallic plates are placed as shown in the Figure. Plate 2 is given a charge Q. All other plates are neutral. Now plates 1 and 4 are earthed. Area of each plate is A.
(a) Find charge appearing on right side of plate 3.
(b) Find potential difference between plates 1 and 2.
View SolutionFigure shows an arrangement of four identical rectangular plates A,B,C, and D each of area S. Find the charges appearing on each face (from left to right) of the plates. Ignore the separation between the plates in comparison to the plate dimensions.

View SolutionFigure shows an arrangement of four identical ractangular plates A, B ,C and D each of area S. Find the charges appearing on each face (from left to right) of the plates. Ignore the separation between the plates in comparison to the plate dimensions.
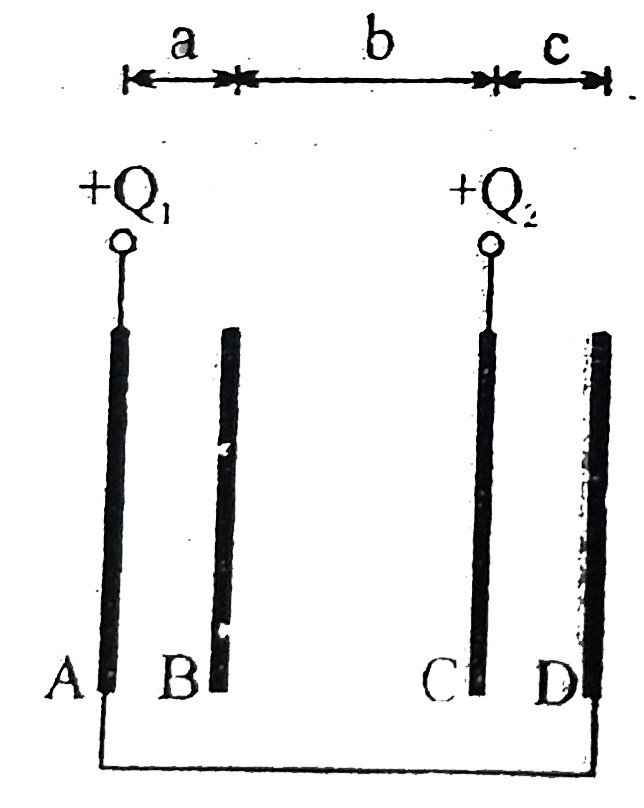
View Solution
