Find the flux of the electric field through each of the five surfaces of the inclined plane as shown in figure. What is the total flux through the entire closed surface?

Video Solution
Text Solution
Note that flux through the face ABF, CDE, and BCEF is zero. Area vector of face ABF points in the positive z- directions area vector of CDF points in the negative z-direction, and area vector of BCEF points in the negative y- direction. In all the three cases, field E is normal to area vector.
Flux through face ABCD
Magnitude of area vector of face ABCD = ab
ϕE=→E⋅→A=E(ab)cos(90∘−θ)=Eabsinθ
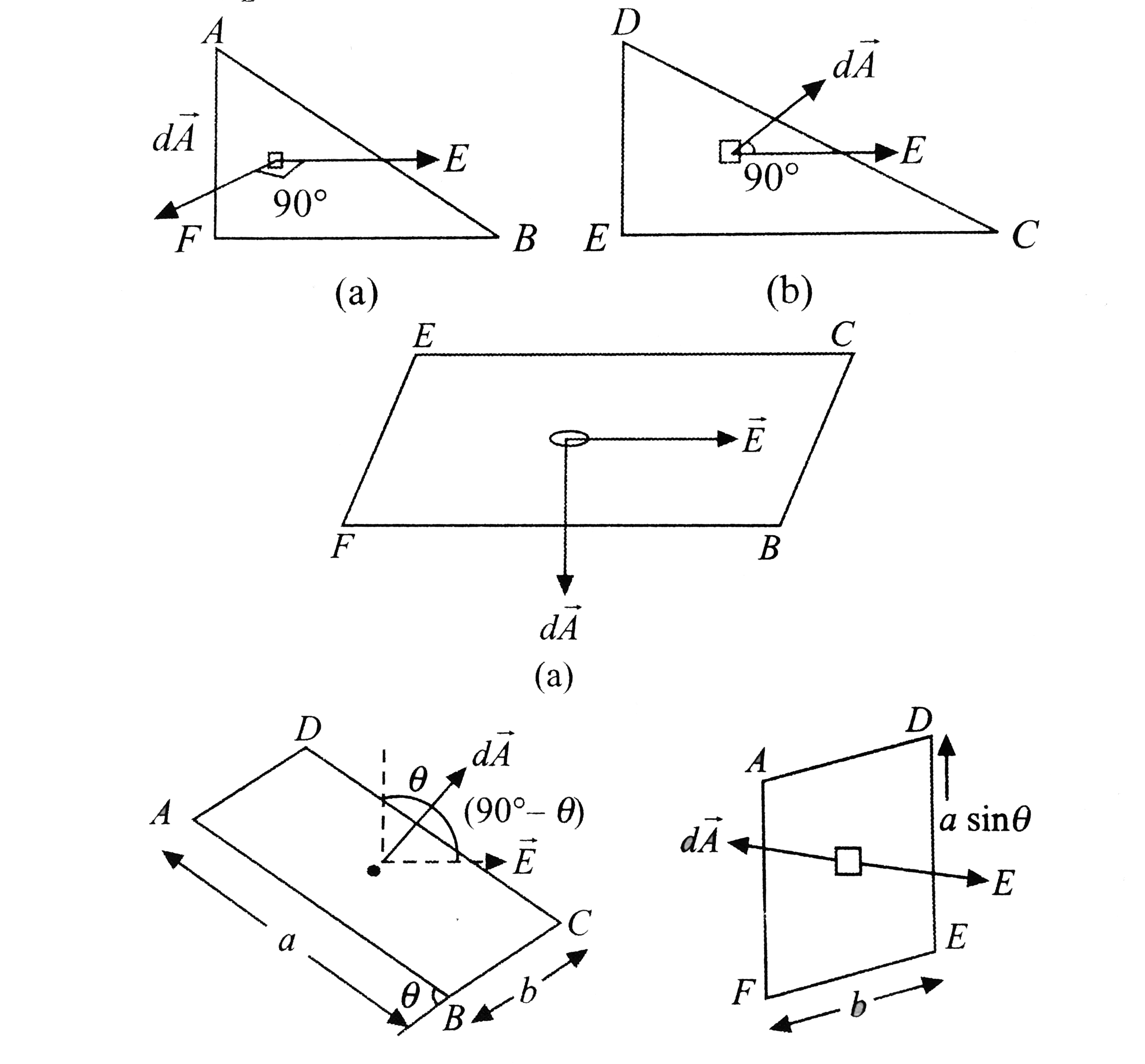
Flux through face ADEF :
Magnitude of area vector of face
ADFE = (asinθ)b=absinθ
ϕE=Ecos180∘'(absinθ)=−Eabsinθ
Thus, we obtain
(ϕE)ABF=0,(ϕE)CDE=0,(ϕE)BCEF=0
(ϕE)ABCD=+Eabsinθand(ϕE)ADEF=−E∣∣∣∫∣∣∣hη.
Flux is a scalar quantity, therefore the total flux is algebraic
sum of flux through each surface.
ϕtotal=(ϕE)ABF+(ϕE)CDE+(ϕE)BCEF
+(ϕE)ABCD+(ϕE)ADEF
=0+0+0+E|∈|θ−Eabsinθ=0 .
|
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Example
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Exercise 2.1
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
Knowledge Check
The electric flux through the surface
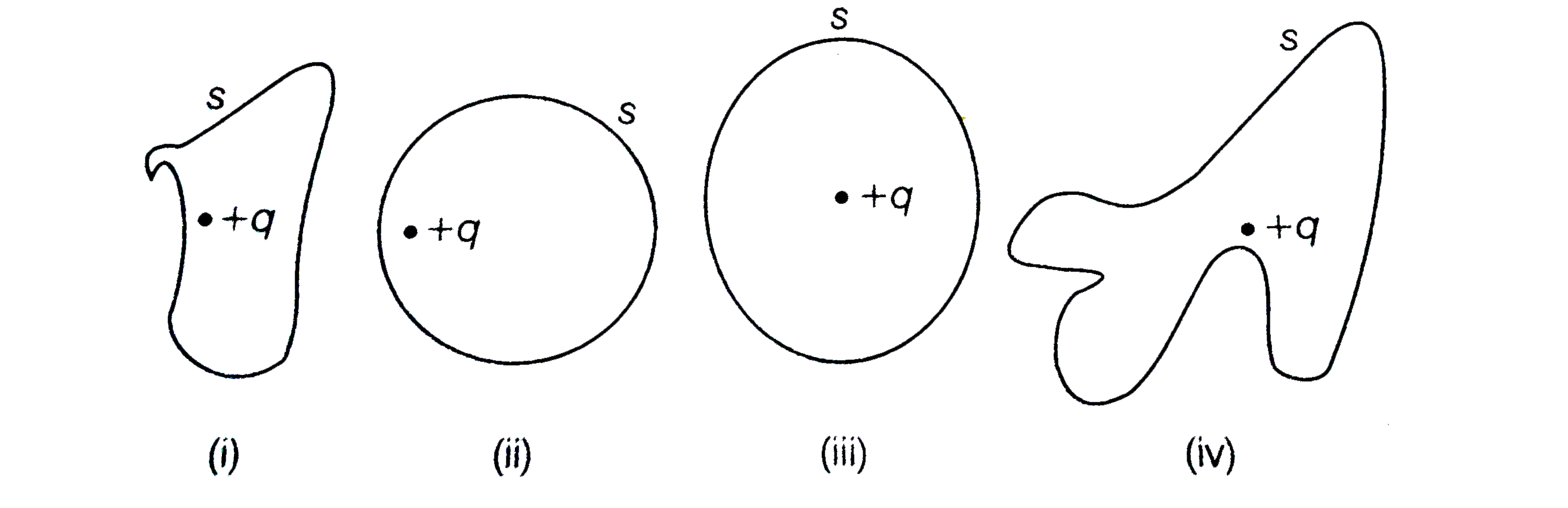 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.If the net electric flux through a closed surface is zero, then we can infer
Ano net charge is enclosed by the surfaceBuniform electric field exists within the surfaceCelectric potential varies from point to point inside the surfaceDcharge is present inside the surface
Find flux through the hemispherical surface
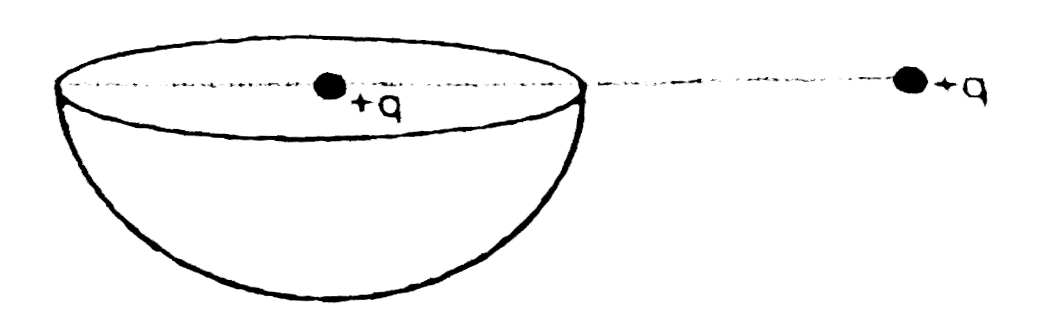
View SolutionFind flux through the hemispherical surface

View SolutionFind out flux through the given Gaussian surface.

View SolutionFind the flux of point charge q through the square surface ABCD as shown
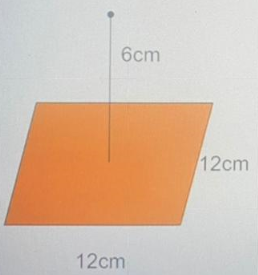
View SolutionThe flux of electric field due to these charges through the surface S is

View Solution