Three identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
To find the intensity of the electric field at the vertex of a regular tetrahedron formed by three identical positive charges Q arranged at the vertices of an equilateral triangle with side length a, we can follow these steps:
Step 1: Understand the Configuration
We have three identical positive charges Q located at the vertices of an equilateral triangle. The fourth vertex of the tetrahedron is directly above the centroid of this triangle.
Step 2: Calculate the Electric Field Due to One Charge
The electric field E due to a single charge Q at a distance r is given by:
E=kQr2
where k=14πϵ0.
In our case, the distance from each charge to the vertex of the tetrahedron (which is directly above the centroid of the triangle) needs to be calculated.
Step 3: Determine the Height of the Tetrahedron
The height h of the tetrahedron can be found using the relationship in a regular tetrahedron:
h=√23a
where a is the side length of the tetrahedron.
Step 4: Calculate the Distance from Each Charge to the Vertex
The distance from each charge to the vertex of the tetrahedron is the hypotenuse of a right triangle where one leg is the height h and the other leg is the distance from the centroid of the triangle to a vertex, which is a√3:
d=
⎷h2+(a√3)2
Substituting h:
d=
⎷(√23a)2+(a√3)2=√23a2+13a2=√a2=a
Step 5: Calculate the Electric Field from Each Charge
Now, the electric field E due to one charge Q at the distance d=a is:
E=kQa2
Step 6: Find the Vertical Component of the Electric Field
The electric field has both vertical and horizontal components. The vertical component Ev can be calculated using the angle θ formed with the vertical:
Ev=Ecosθ
where cosθ=hd=√23aa=√23.
Thus,
Ev=kQa2⋅√23
Step 7: Calculate the Net Electric Field
Since there are three charges, the total vertical component of the electric field at the vertex of the tetrahedron is:
Enet=3Ev=3(kQa2⋅√23)=3kQ√23a2
Final Expression
Thus, the intensity of the electric field at the vertex of the tetrahedron is:
Enet=3kQ√2a2√3=3√2kQa2√3
We have three identical positive charges Q located at the vertices of an equilateral triangle. The fourth vertex of the tetrahedron is directly above the centroid of this triangle.
The electric field E due to a single charge Q at a distance r is given by:
E=kQr2
where k=14πϵ0.
The height h of the tetrahedron can be found using the relationship in a regular tetrahedron:
h=√23a
where a is the side length of the tetrahedron.
The distance from each charge to the vertex of the tetrahedron is the hypotenuse of a right triangle where one leg is the height h and the other leg is the distance from the centroid of the triangle to a vertex, which is a√3:
d=
⎷h2+(a√3)2
d=
⎷(√23a)2+(a√3)2=√23a2+13a2=√a2=a
Now, the electric field E due to one charge Q at the distance d=a is:
E=kQa2
The electric field has both vertical and horizontal components. The vertical component Ev can be calculated using the angle θ formed with the vertical:
Ev=Ecosθ
where cosθ=hd=√23aa=√23.
Ev=kQa2⋅√23
Since there are three charges, the total vertical component of the electric field at the vertex of the tetrahedron is:
Enet=3Ev=3(kQa2⋅√23)=3kQ√23a2
Thus, the intensity of the electric field at the vertex of the tetrahedron is:
Enet=3kQ√2a2√3=3√2kQa2√3
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
Two charge +Q,−Q are placed at the two verticels of an equilateral triangle of side 'a'. Then the intensity of electric field at the third vertex is
View SolutionTwo charge +Q each are placed at the two verticles of an equilateral triangle of side a .The intensity of electric field at the third vertex is
View Solution
Knowledge Check
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
A2Kq2r2BKq22r2C√3Kq2r2DKq2√2r2Three poistive charges of equal value q are placed at the vertices of an equilateral triangle. The resulting lines of force should be sketched as in
A(a)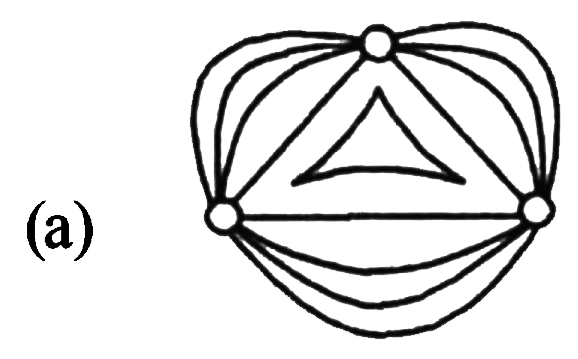 B(b)
B(b) C(c)
C(c)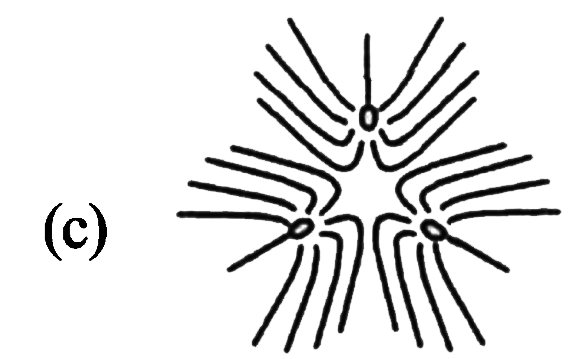 D(d)
D(d)
Three charges are arranged on the vertices of an equilateral triangle as shown in figure (29.E6) find the dipole moment of the combination.

View SolutionThree points charges =q, -2q, +q are arranged on the vertices of an equilaterial triangle as shown in the figure. Find he dipole moment of the system.
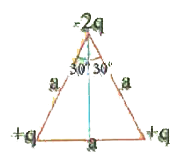
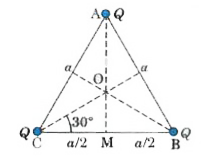
View SolutionThree identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThree identical point charges, q, are placed at the vertices of an equilateral triangle as shown in the figure. The length of each side of the triangle is d. Determine the magnitude and direction of the total electrostatic force on the charge at the top of the triangle.
View Solution
