Two identical balls each having a density $ρ$ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle $θ$ with vertical. Now, both the balls are immersed in a liquid. As a result the angle $θ$ does not change. The density of the liquid is $σ$ . Find the dielectric constant of the liquid.

Video Solution

Text Solution

Verified by Experts

Let V be the volume of each ball, then the mass of each ball is $m = \propto V$ .When the balls are in air, from the previous problem.
$F = m g \tan θ = ρ V g \tan θ$ ...(i)
,
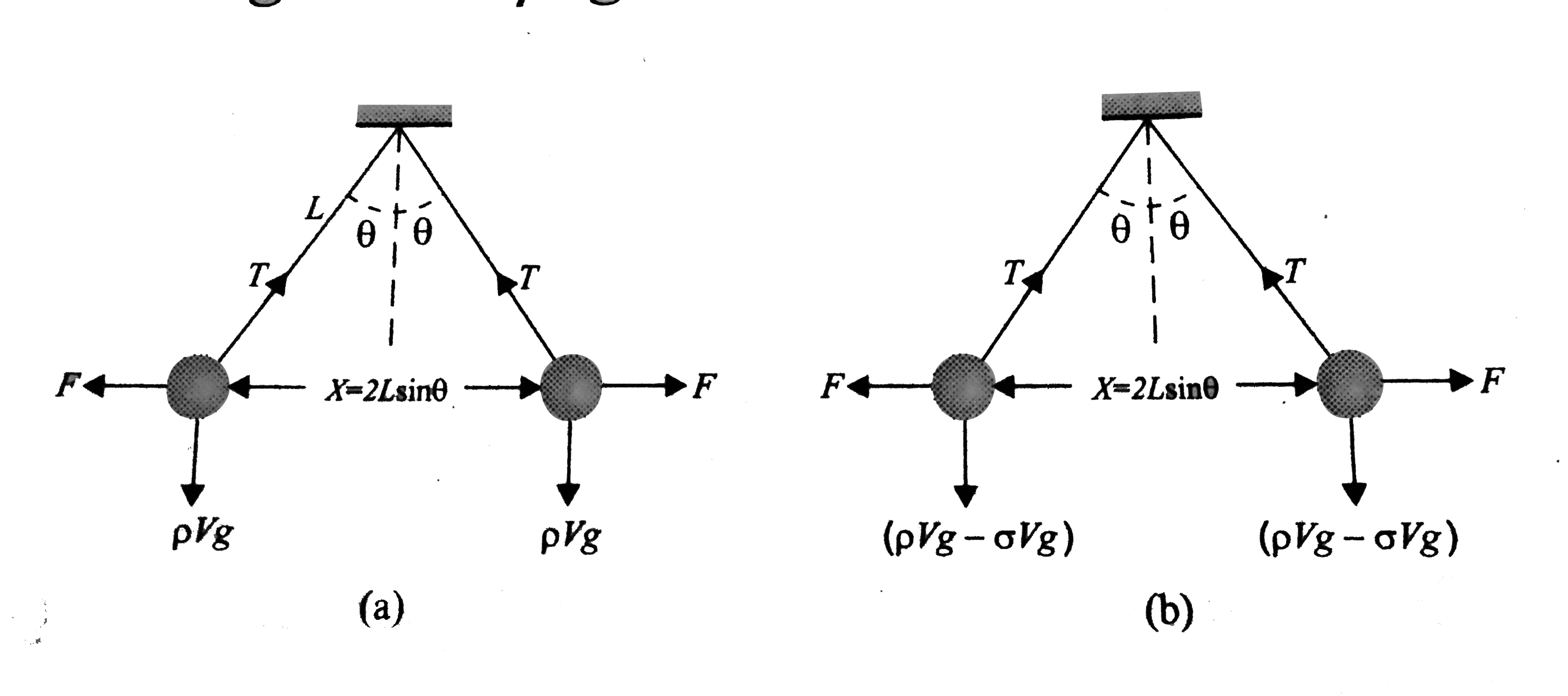when the balls are suspended in liquid, the Coulombic force is reduced to $F' = F / K$ and apparent weight=weight -upthrust, i.e
$W' = ρ V g - σ V g$
According to the problem, angle $θ$ is unchanged therefore.
$F' = W' \tan θ = (ρ V g - σ V g) \tan θ$ ...(ii)
From Eqs, (i) and (ii) we get
$\frac{F}{F'} = K = \frac{ρ V g}{ρ V g - σ V g} = \frac{ρ}{ρ - σ}$ .

Updated on:21/07/2023

Two small identical balls are suspened from a common point by two identical strings. When they are given identical charges, they move apar and the strings make with the vertical an angle of q. Now the system is immersed in a liquid and as a result the angle q does not change. If r is the density of the material of the balls and s is the density of the liquid, the dielectric constant of the liquid is
A $\frac{p}{p - σ}$
B $\frac{p - σ}{p}$
C $\frac{σ}{p - σ}$
D $\frac{p - σ}{σ}$
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?
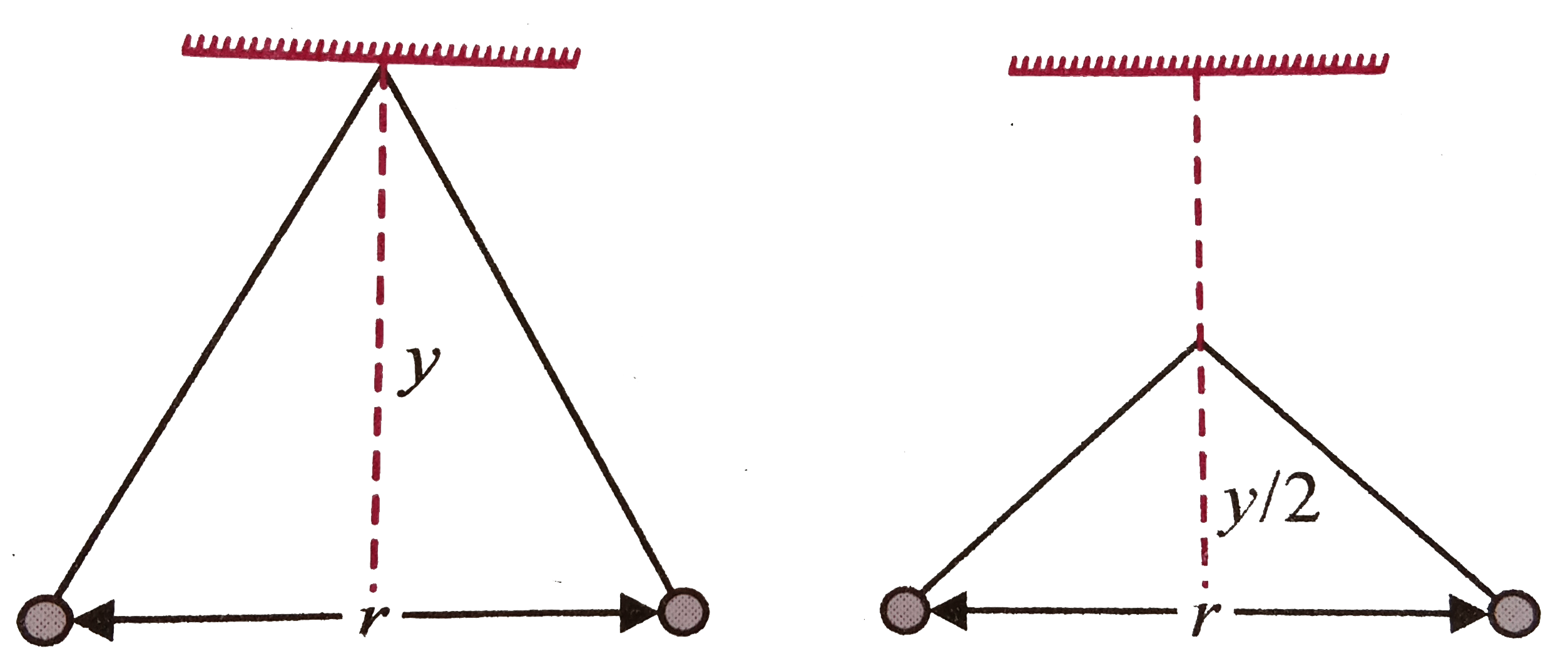
A $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 2}$
B $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 3}$
C $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g})}^{1 / 3}$
D $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g^{2}})}^{1 / 3}$
Two path balls carrying eqaul chareges are suspended froom a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :

A $(\frac{2 r}{3})$
B ${(\frac{1}{\sqrt{2}})}^{2}$
C $(\frac{r}{\sqrt[3]{2}})$
D $(\frac{2 r}{\sqrt{3}})$