A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: λ1=3650A∘,λ2=4047A∘,λ3=4358A∘,λ4=5461A∘,λ5=6907A∘ The stopping voltages, respectively were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V.
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.Solution in Telugu
Given, λ1=3650Å=3650×1010m λ4−5461Å
λ2=4047Å=4047×10−10m λ5=6907Å=6907×10−10m
λ3=4358Å=4358×10−10m
V01=1.28V,V02=0.95,V03=0.74V,V04=0.16V,V05=0
(a) v1=cλ1=3×1083650×10−10=8.219×1014 v4cλ4=3×1085461×10−10=5.493×1014 Hz
v2=cλ2=3×1084047×10−10=7.412×1014Hz v5=cλ5=3×1086907×10−10=4.343×1014Hz
v3=cλ3=3×1084358×10−10=6.884×1014Hz
As we know that eV0=hv−ϕ0
V0=hve=ϕ0e
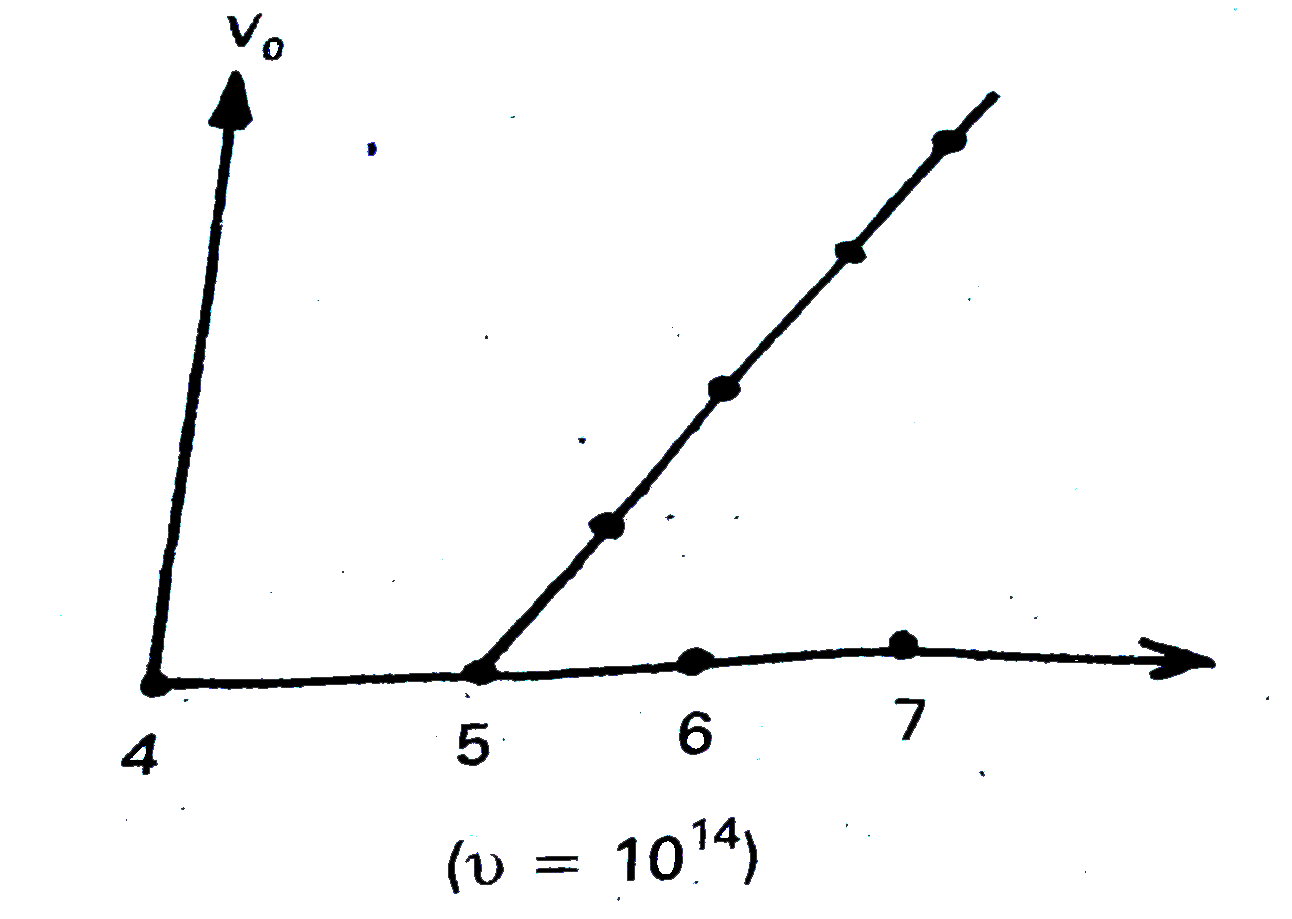
As the graph between V0 and frequency v is a straight line :
The slope ofthis gives the values of he
h=1.12×1.6×10−192.726×104=6.674×10−34 J-s
(b ) ϕ0=hv0=6.574×10−34×5×1014
=32.870×10−20J=32870×10−201.6×10−19eV
= 2.05 eV
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:DUAL NATURE OF RADIATION AND MATTERExercise:DAM SURE (VSAQ)
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:DUAL NATURE OF RADIATION AND MATTERExercise:TEXTUAL EXERCISES
Explore 34 Videos
- CURRENT ELECTRICITY Book:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:CURRENT ELECTRICITY Exercise:ADDITIONAL EXERCISES
Explore 22 Videos
- ELECTRIC CHARGES AND FIELDSBook:VIKRAM PUBLICATION ( ANDHRA PUBLICATION)Chapter:ELECTRIC CHARGES AND FIELDSExercise:DAM SURE LAQ
Explore 1 Video
Similar Questions
The wavelength of electromagnetic radiation is doubled. What will happen to the energy of the photons of the new radiation ?
View SolutionFind the
(a) maximum frequency, and
View SolutionThe earth's surface has a negative surface charge density of 10−9Cm−2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low condutivity of the lower atmosphere) in a current of only 1800 A over the entire globe. if there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth's surface (This never happens in parctice there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth =6.3×106m)
View SolutionState Gauss's law in electrostatics. Applying Gauss's law derive the expression for electric intensity due to an infinite plane sheet of charge.
View SolutionA mercury lamp is a convenient souce for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red vissible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: λ1=3650A∘,λ2=4047A∘,λ3=4358A∘,λ4=5461A∘,λ5=6907A∘ The stopping voltages, respectively were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V.
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.
View SolutionCut off potential for a metal in photoelectric effect for light of wavelength λ1,λ2 and λ3 is found to be V1,V2 and V3 volts , If V1,V2 and V3 are in Arithmetic progression then λ1,λ2 and λ3 will be in
View SolutionThe wavelengths and frequencies of photons in transition 1,2 and 3 for hydrogen like atom are lambda_(1),lambda_(2),lambda_(3), v_(1),v_(2) and v_(3) respectively. Then:
View SolutionThe stopping potential are V_(1) and V_(2) . Calculate the (V_(1)-V_(2)) , if the lambda_(1) and lambda_(2) are wavelength of incident lights, respectively.
View Solutionएक पारद लैंप, प्रकाश विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्त्रोत है क्योंकि यह दृश्य –स्पेक्ट्रम के परबैंगनी (UV) के लाल छोर तक कइ वर्ण रेखाएं उत्सर्जित करता हैं। रूबीडियम प्रकाश सेल के हमारे प्रयोग में पारद स्त्रोत की निम्न वर्ण रेखाओं का प्रयोग किया गया
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å,
निरोधी वोल्टताएं क्रमशः निम्न मापी गई
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
(a) प्लैंक स्थिरांक h का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य फलन का आकलन कीजिए।
View Solutionएक पारद लैंप, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है, क्योकिं यह दृश्य-स्पेक्ट्रम के पराबैगनी (UV) से लाल छोर तक कई-वर्ण रेखाएँ उत्सर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया :
λ1=3650Å,λ2=4047+Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गई :
V01=1⋅28V,V2=0⋅95V,V03=0⋅74V,V04=0⋅16V,V05=0V
प्लैंक स्थिरांक h का मान ज्ञात कीजिए।
[ नोट : उपयुर्क्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e=1.6x10−19C की आवश्यकता होगी। इस प्रकार के प्रयोग Na,Li,K आदि के लिए मिलिकन ने किए थे। मिलिकन ने अपने तेल-बूँद प्रयोग से प्राप्त e के मान का उपयोग कर आइंस्टाइन के प्रकाश-विद्युत समीकरण को सत्यापित किया तथा इन्ही प्रेक्षणों से h के मान के लिए पृथक अनुमान लगाया। ]
View SolutionCut off potentials for a metal in photoelectric effect for light of wavelength lambda_(1), lambda_(2) and lambda_(3) is found to be V_(1), V_(2) and V_(3) volts if V_(1), V_(2) and V_(3) are in Arithmetic Progression and lambda_(1), lambda_(2) and lambda_(3) will be :
View SolutionIf the velocity and wavelength of light in air is Va and λa and that in water is Vw and λw then the refractive index of water is,
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å,
The stopping voltages, respectively, were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6×10−19C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å,
The stopping voltages, respectively, were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6×10−19C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the Uv to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used: lambda_(1) = 3650 Å, lambda_(2) = 4047 Å, lambda_(3) = 4358 Å, lambda_(4) = 5461 Å, lambda_(5) = 6907 Å , The stopping voltages, respectively, were measured to be: V_(01) = 1.28 V, V_(02) = 0.95 V, V_(03) = 0.74 V, V_(04) = 0.16 V, V_(05) = 0 V Determine the value of Planck’s constant h, the threshold frequency and work function for the material. [Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 xx 10^(-19) C ). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red and end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
The stopping voltages, respectively, were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
Determine the value of Planck's constant h, the threshold frequency and work function for the material.
View Solution

