Two students analysed two different problems off mechanics involving constraint motion. Symbols have their usual meaning.
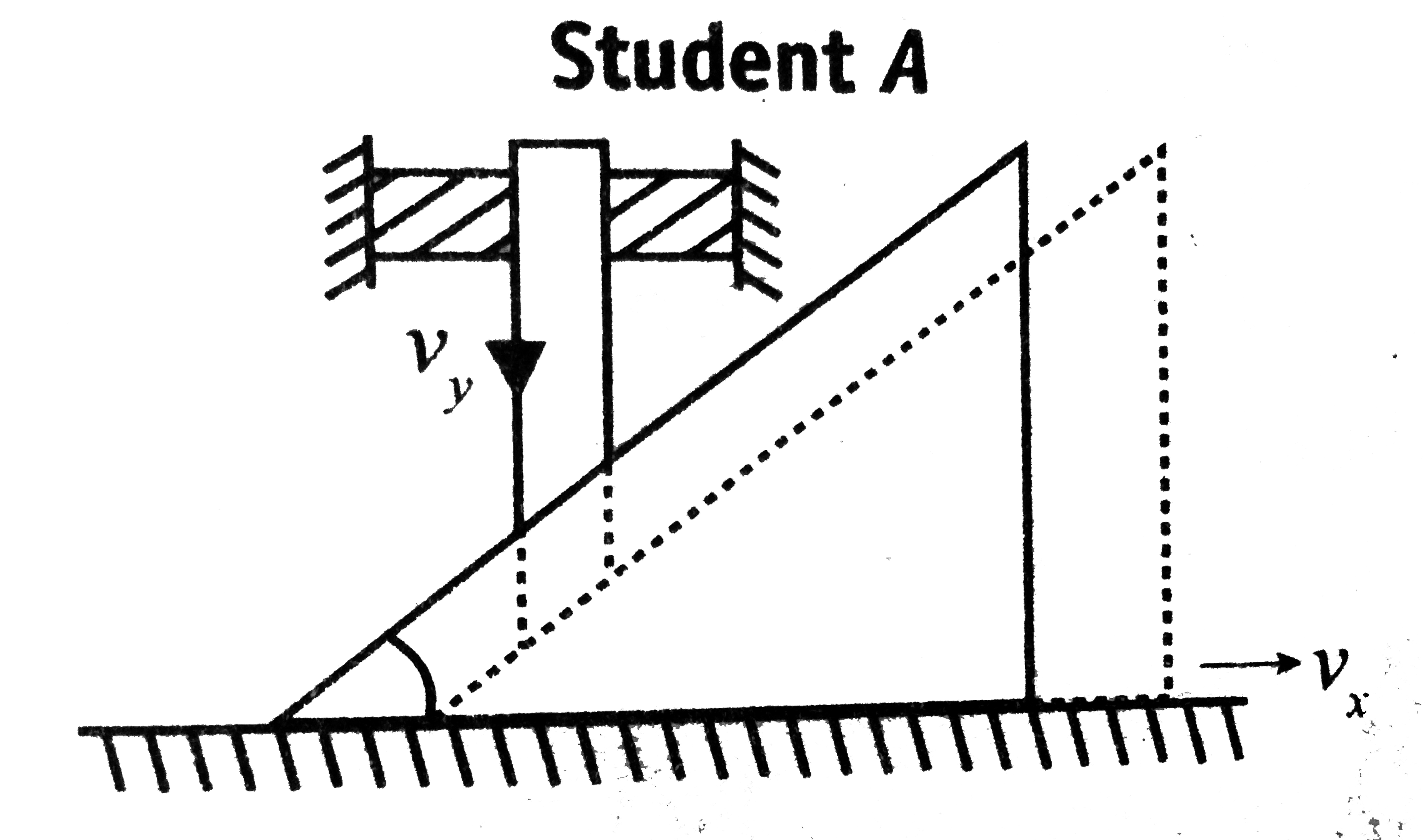
The vertical rod can move only vertically and the wedge can move only horizontally.
yx=tanθ,y=xtanθ,vy=vxtanθ
Student B.
The ends of the rods are slipping on the ground and the wall, respectively
yx=tanθ,y=xtanθ,vy=vxtanθ

Student A is correct B is wrong
Student A is wrong B is correct
Both are correct
Both are wrong
The correct Answer is:A

Displacement along the common normal will be the same. 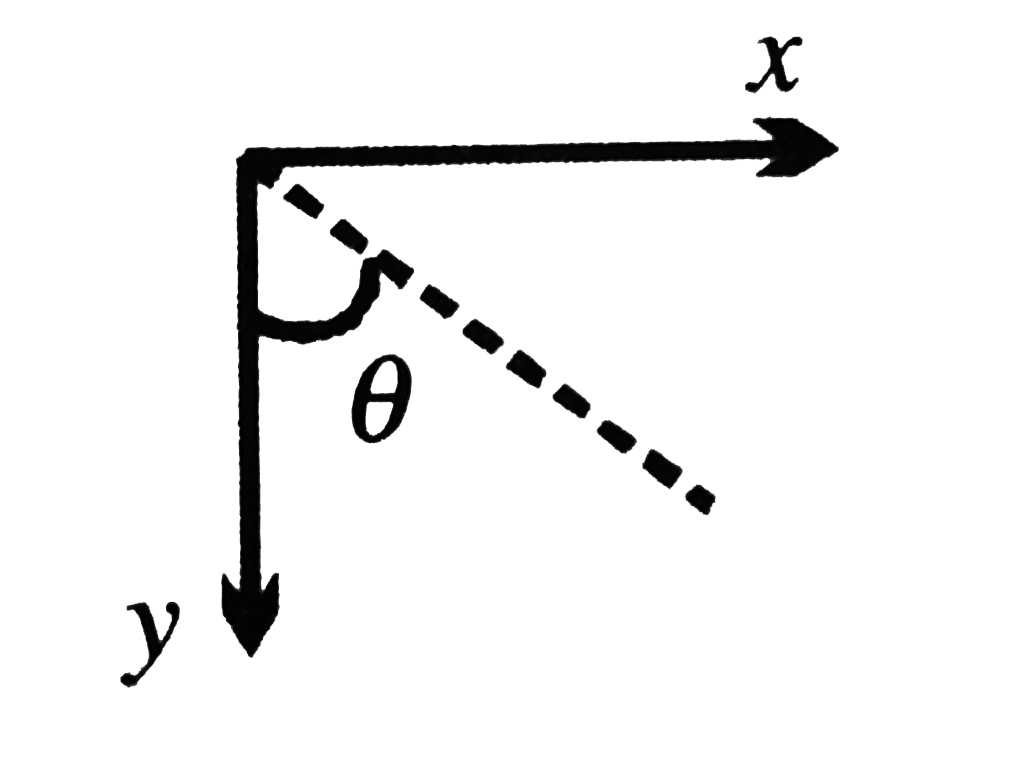
ycosθ=xsinθ⇒y=xtanθ. Differentiating both sides, vy=vxtanθ.
Velocity of the two ends of the rod will be the same along the rod. 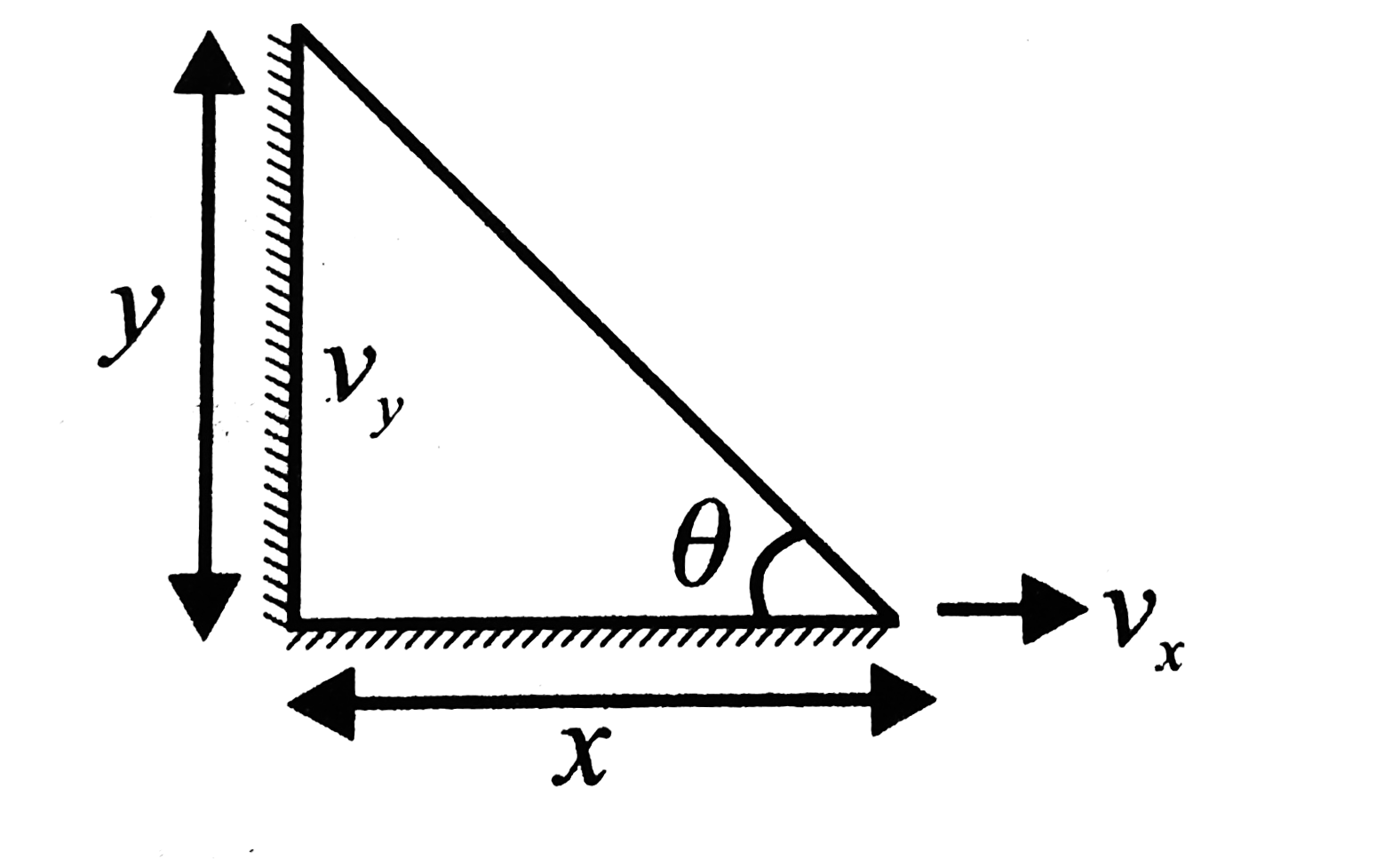
vysinθ=vxcosθ
⇒vy=vxcotθ
Student A is correct and B is wrong.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:MCQ_TYPE
Explore 20 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:LC_TYPE
Explore 34 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
Similar Questions
A rod od length l is moving in a vertical plane (x−y) when the owest point A of the rod is moved with a velociy v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View Solution
Knowledge Check
In a projectile motion let vx and vy are the horizontal and vertical components of velocity at any time t and x and y are displacements along horizontal and vertical from the point of projection at any time t.Then
Avy−t graph is a straight line with negative slope and positive interceptBx−tgraph is a straight line passing through originCy−t graph is a straight line passing through originDux−t graph is a straight lineIf A(2, -3) and B(-2, 1) are two vertices of a triangle and third vertex moves on the line 2x + 3y = 9, then the locus of the centroid of the triangle is
A2 x - 3y = 1Bx - y = 1C2x + 3y = 1D2 x + 3y = 3If two lines of Regression are respectively y=ax+b and x=αy+β. If the two variables have the same mean, then b/β=
A1+a1+αB1+α1+aC1−a1−αD1−α1−a
A rod AB of length 4 units moves horizontally with its left end A always on the cirele x2+y2−4x−18y−29=0 then the locus of the other end B is
View SolutionVx and Vy are the horizontal and vertical compounds of velocity with x and y as the corresponding displacements along horizontal and vertical at any time t in a projectile motion in XY co-ordinate system, where g is the acceleration due to gravity.

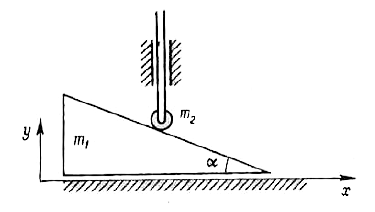
View SolutionA rod of mass m2 rests on wedge of mass m1 (Fig.). Guides allow the rod to move only in the direction of the y-axis and the wedge only in the direction of the x-axis. Find the acceleration of both bodies and the reaction of the wedge. Neglect friction.
View SolutionTwo rods of lengths aandb slide along the x− and y−aξs, respectively, in such a manner that their ends are concyclic. Find the locus of the center of the circle passing through the endpoints.
View SolutionA body is projected horizontally from a point above the ground. The motion of the body
is described by the equations x = 2 t and y=5t2 where x and y are the horizontal and vertical displacements (in m) respectively at time t. What is the magnitude of the velocity of the body 0.2 second after it is projected?
View Solution

