A uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
In this case, different part of the rod does not elongate to the same extent. The element closer to the support elongates more as the stress is higher with respect to the elements closer to the free end of the rod.
To determine total elongation of the rod,let us consider a small element of defferential length dx at a distance x from the free end of the rod, as shown in the figure.

The stress at the position of this element is produced by the weight of the rod of length x lying below it i.e. (WL)x
Therefore, stress at this section
σ=(WL)xA=WxAL
The elongation dδ produced in the differential element dx is
dδ=σYdx=WYALxdx
Thus, total elongation produced in the rod can be calculated as
δ=∫dδ
δ=SYAL∫L0xdx=WYAL[x22]L0
or σ=12WLYA.........v
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A uniform heavy rod of weight 10 kg ms−2, cross-sectional area 100 cm2 and length 20 cm is hanging from a fixed support. Young modulus of the material of the rod is 2×1011Nm−2 Neglecting the lateral contraction, find the elongation of rod due to its own weight:
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View Solution
Knowledge Check
A unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cmA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
A12ρgLB14ρgLCρgLDNone of theseA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
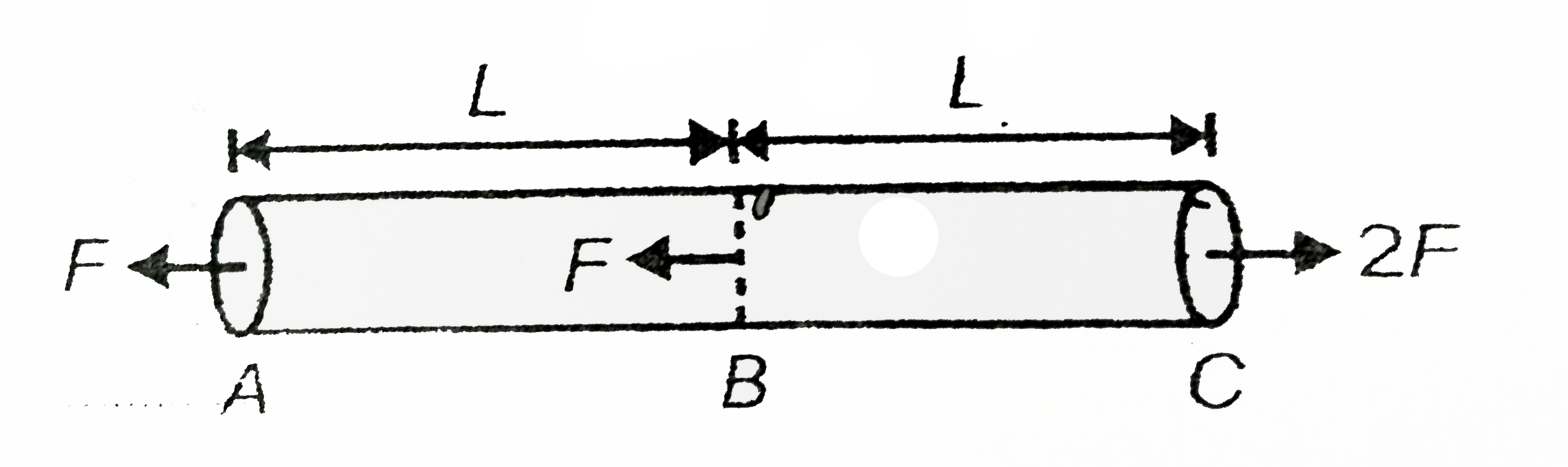
Select the correct alternatives.
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.
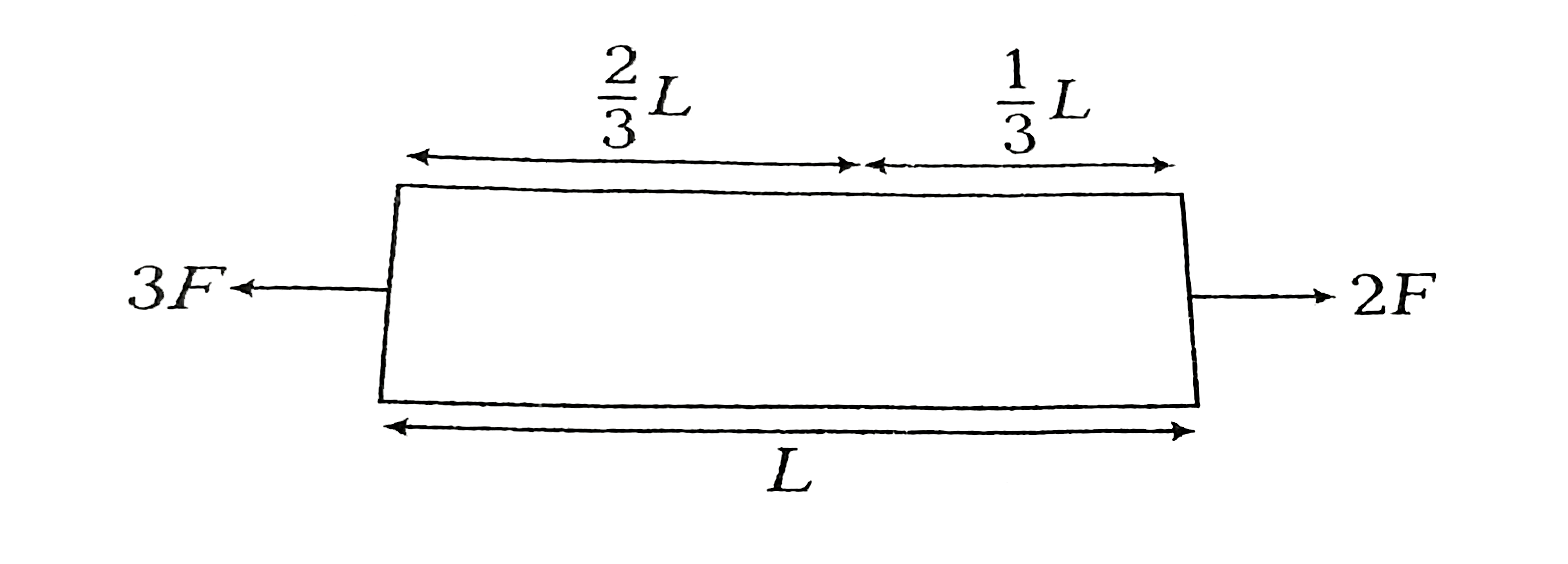
The elongation produced in the rod is
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
View SolutionA metallic rod of length l and cross - sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y, then the work done is proportional to
View Solution