A metal piece of mass 160 g lies iln equilibrium inside a glass of water figure. The ppece touches the bottom of the glass at a small number of points. If the density of the metl is 8000 kg m−3, find the normal fore exerted by the bottom of the glass on the metal piece.

2N
8N
0.16N
1.4N
The correct Answer is:D
As the piece touches the glass at small number of points, water would be there at the bottom of the piece also and hecne buoyancy acts on it.
From equilibrium condition mg=FB+N
FB=Vρwaterg=mρmetal×ρwater×g
=0.168×10=0.2N
So, N=mg−FB=1601000×10−0.2=1.4N
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
When a metallic sphere is released from the surface of water filled in a container of uniform area of cross section it is found to reach the bottom of the container in 2 s. If the density of the material of the sphere is 4.9gcm−3, calculate the pressure exerted by the liquid at the bottom of the container. Assume that only gravitational force and up-thrust act on the body.
View SolutionWhen a metallic sphere is released from the surface of water filled in a container of uniform area of cross section it is found to reach the bottom of the container in 2 s. If the density of the material of the sphere is 4.9gcm−3, calculate the pressure exerted by the liquid at the bottom of the container. Assume that only gravitational force and up-thrust act on the body.
View Solution
Knowledge Check
A swimming pool has the dimensions shown in the figure . It is filled with water to a uniform depth of 8.00 m . The density of water = 1.00×103kg/m3
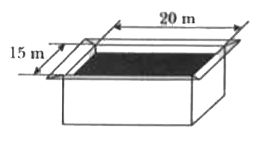
What is the total force exerted on the bottom of the swimming pool ?A2.40×107NB5.90×107NC5.40×107ND7.50×107 NA small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
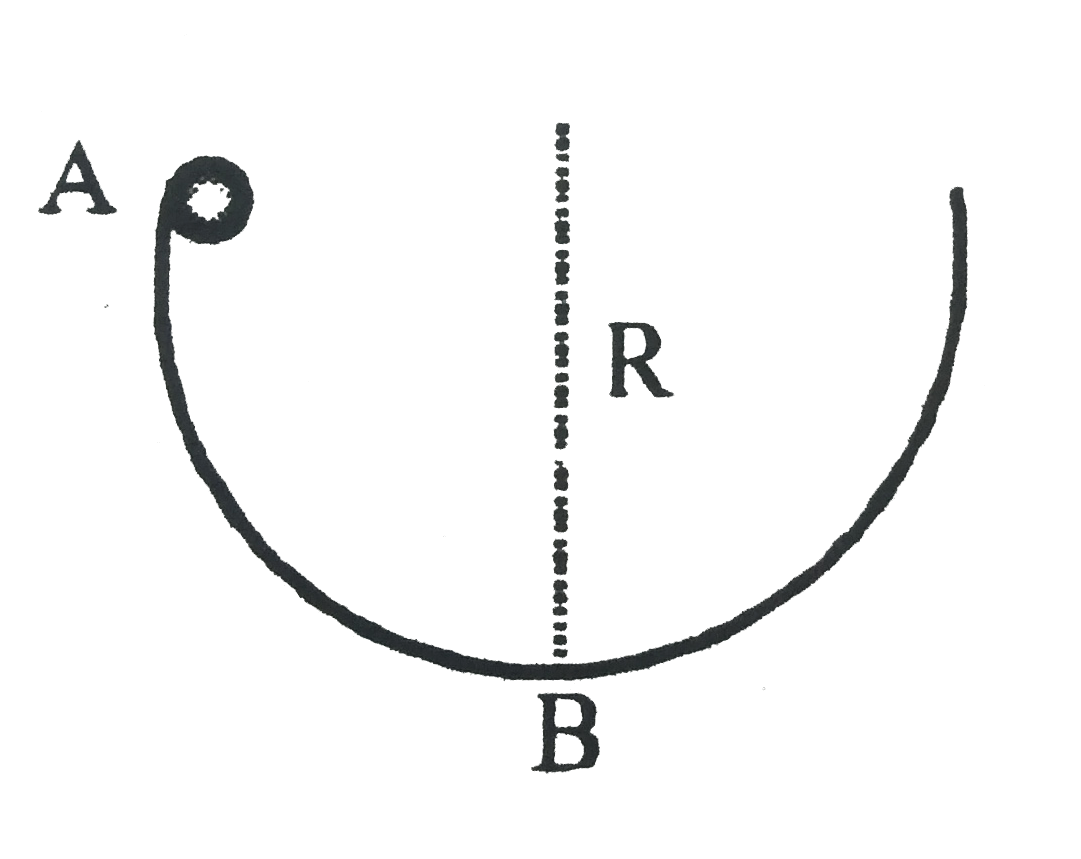 .A107mgB177mgC57mgD75mg
.A107mgB177mgC57mgD75mgA swimming pool has the dimensions shown in the figure . It is filled with water to a uniform depth of 8.00 m . The density of water = 1.00×103kg/m3
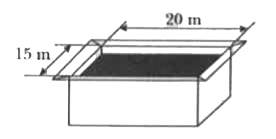
What is the total pressure exerted on the bottom of the swimming pool ?A0.79×105 PaB1.80×105 PaC1.48×105 PaD1.97×105 Pa
A glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
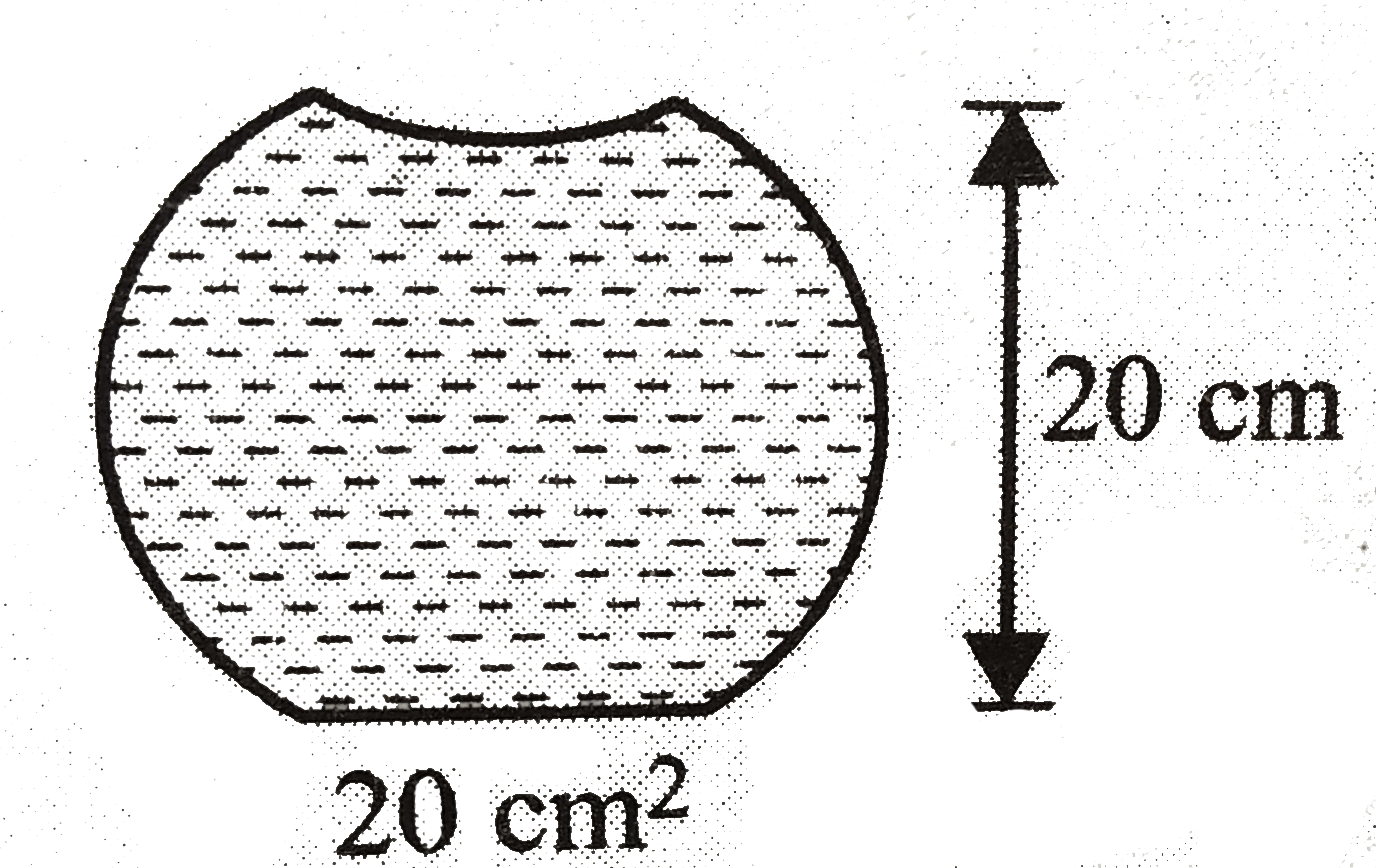
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View SolutionA curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View SolutionA glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.
View SolutionA glass beaker of mass 400 kg floats in water with the open end just touching the surface of water and half of the beaker filled with water. The inner volume of the beaker is 500cm3 What is the density of the meterial of the beaker ?
View Solution

