Water is retained by a curved gate AB. Compute the horizontal and vertical component of the resultant of the hydrostatic pressure dsitribution on the gate AB, which is a quarter of a cylinder. Assume that the gate is 4m wide.

a. Horizontal component. The horizontal component of the resultant force on the gate is equal to the force on the vertical projection BA' of the gate. The pressure at a depth y from the free surface of the water is P=ρgy. The force on the strip of area 4dy of the gate is ,
dFH=P(4dy)=ρgy(4dy)=4ρydy

Total horizontal force is
FH=4ρg∫1510ydy=4ρg∣∣∣y22∣∣∣1510
=4×1000×10(152−1022)=250×104N
b. Vertical component : It is equal to the weight of the water above the curved surface. Dividing the volume above the curved surface into a rectangular parallelepiped and a quarder cylinder, we thus have
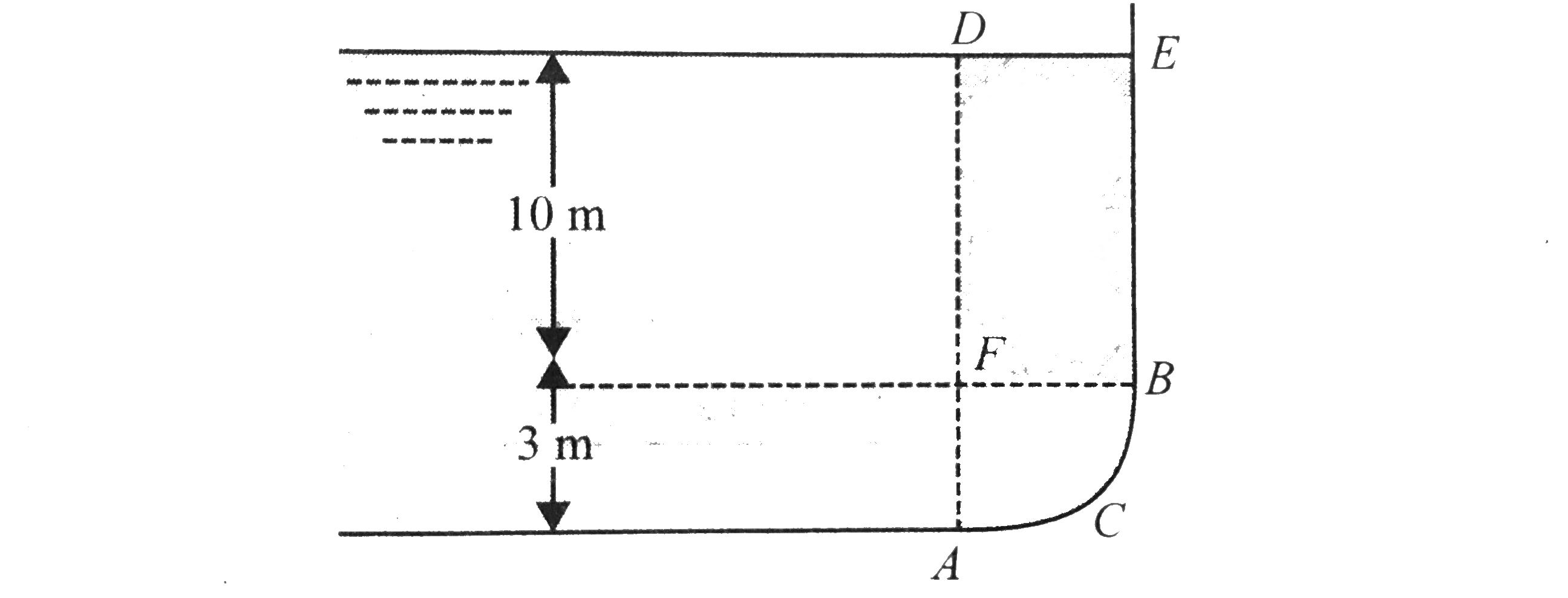
Fv= weight of water in DEFB+ Weight of water in ACBF
=ρ[V1+V2]g=1000[10×4×4+π(5)2×44]×10
[8×π]×104N
After calculating the values of Fv and FH we can calculate the resultant force on the gate F=√F2H+F2V
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Solved Examples
Explore 7 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
During a rainstorm the raindrops are observed to strike the ground at an angle of 37∘ with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed ?
View SolutionA horizontally oriented uniform rod AB of mass m=1.40kg and length l0=100cm rotates freely about a stationary vertical axis OO′ passing through its end A. The point A is located at the middle of the axis OO′ whose length is equal to l=55cm. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis OO′ is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
View Solution
Knowledge Check
A horizontal cylinderical tank 6πm in diameter is half full of water. The space above the water is filled with a pressurized gas of unknown refractive index. A small laser can move along the curved bottom of the water and aims a light beam towards the centre of the water surface. When the laser has moved a distance s=1m or more (measured from curved face) from the lowest point in water, no light enters the gas. The refractive index of gas is (μwater=4/3)
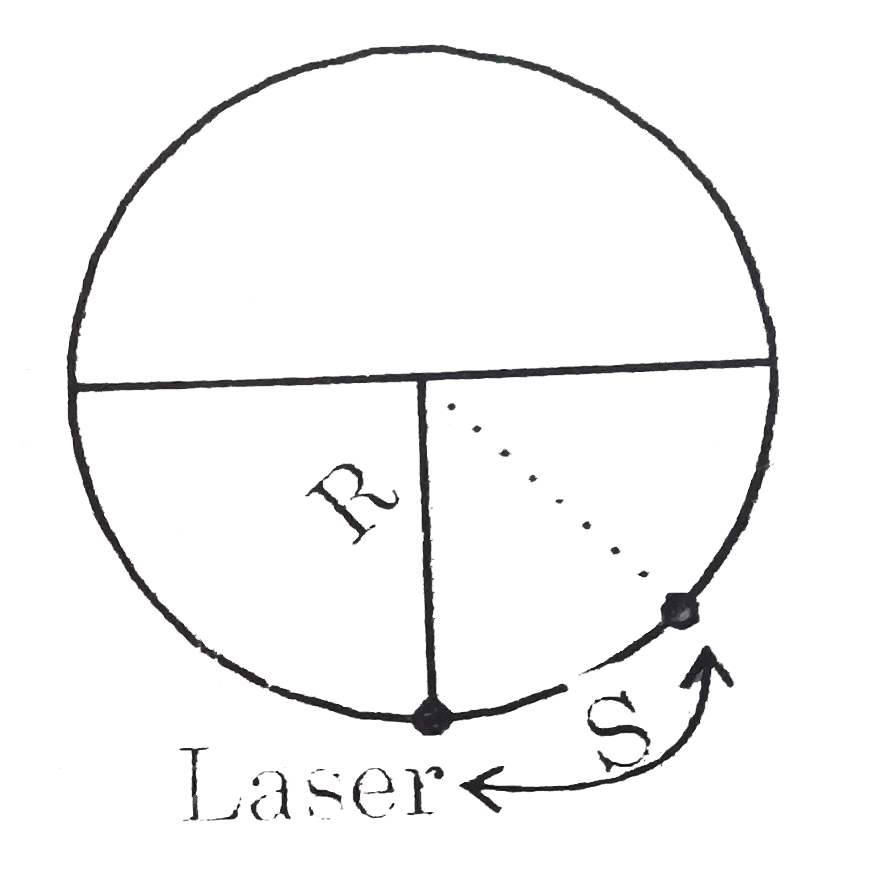 A4/√3B√5/2C2/√3D√3
A4/√3B√5/2C2/√3D√3
A horizontal cylinder closed from one end is rotated with a constant angular velocity ω about a vertical axis passing through the open end of the cylinder. The outside air pressure is equal to p0, the temperature to T, and the molar mass of air to M. find the air pressure as a function of the distance r from the rotate axis. The molar mass is assumed to be independent of r.
View SolutionA particle of mass m is attached to an end of a light rigid rod of length a. The other end of the rod is fixed, so that the rod can rotate freely in vertical plane about its fixed end. The mass m is given a horizontal velocity u at the lowest point. (a) Prove that when the radius to the mass makes an angle θ with the upward vertical the horizontal component of the acceleration of the mass (measured in direction of u) is [g(2+3cosθ)−u2/a]sinθ (b) If 4ag ltu2 lt5ag, show that there are four points at which horizontal component of acceleration is zero. locate the points.
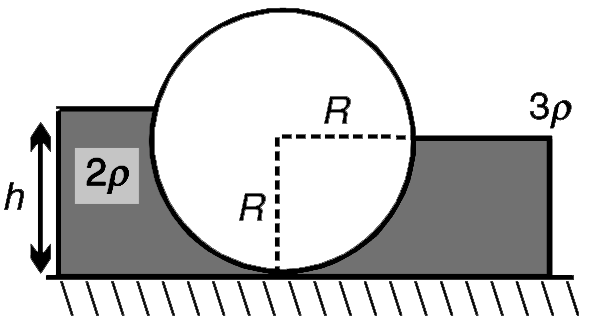
View Solution(i) In the figure shown, the heavy cylinder (radius R) resting on a smooth surface separates two liquids of densities 2ρ and 3ρ. Find the height 'h' for the equilibrium of cylinder.
(ii) The cross section of a dam wall is an arc of a circle of radius R=20m subtending on angle of θ=60∘ at the centre of the circle. the centre (O) of the circle lies in the water surface. The width of the dam (i.e., dimension perpendicular to the figure) is b=10m. Neglect atmospheric pressure is following calculations.
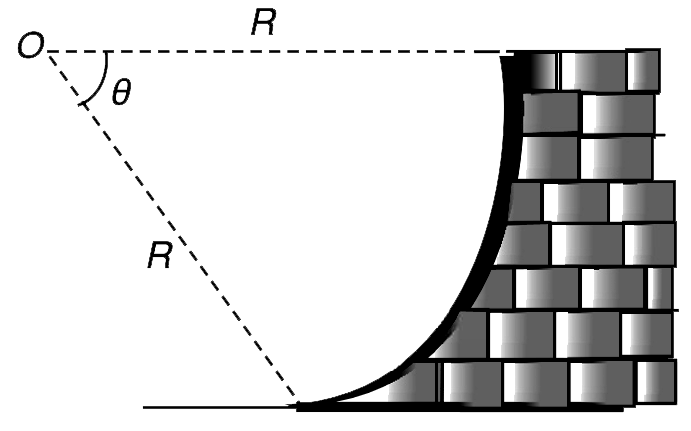
(a) Calculate the vertical component of force (Fx) applied by water on the curved dam wall.
(b) Calculate the horizontal component of force (FH) applied by water on the curved dam wall.
(c) Calculate the resultant force applied by the water on the curved dam wall.
View SolutionTwo metal bars are fixed vertically and are connected on top by a capacitor of capacitance C. A sliding conductor AB can slide freely on the two bars. Length of conductor AB is L and its mass is m. It is connected to a vertical spring of force constant k. The conductor AB is released at time t = 0, from a position where the spring is relaxed. Taking initial position of the conductor as origin and downward direction as positive x axis, write the x co-ordinate of the conductor as a function of time. The entire space has a uniform horizon- tal magnetic field B. Neglect resistance and inductance of the circuit and assume that the bar AB always remains horizontal.
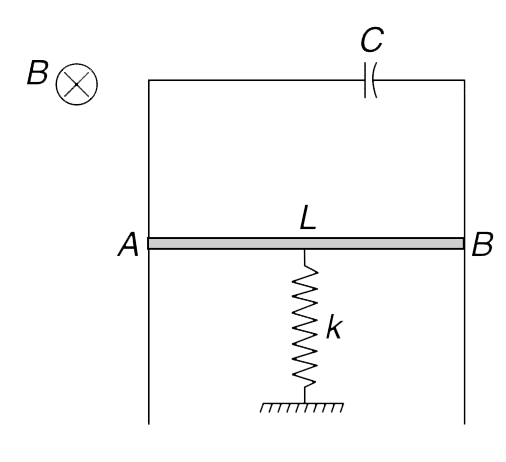
View SolutionA rod AB length 5m which remains in vertical plane has its ends A and B constrained to remain contact with a horizontal floor and a vertical wall respectively. Determine the velocity of the end B and angular velocity at the position shown in Fig. , if the point A has a velocity of 3ms1rightward.

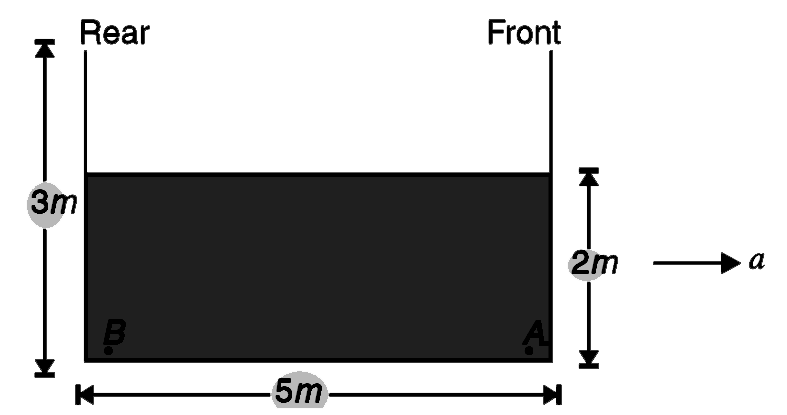
View SolutionAn open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.
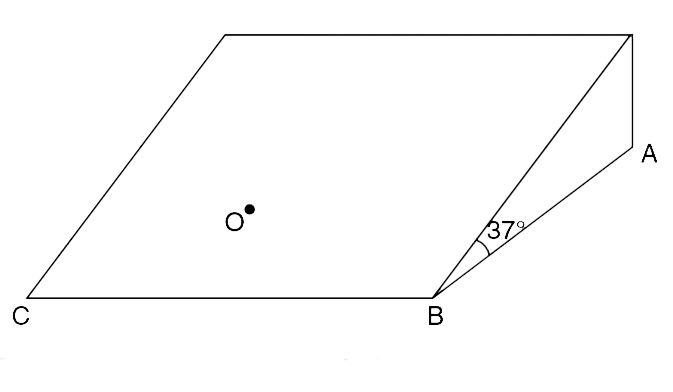
View SolutionThere is a large wedge placed on a horizontal surface with its incline face making an angle of 37∘ to the horizontal. A particle is projected in vertically upward direction with a velocity of u=6.5m/s from a point O on the inclined surface. At the instant the particle is projected, the wedge begins to move horizontally with a constant acceleration of a=4m/s2. At what distance from point O will the particle hit the incline surface if
(i) direction of a is along BC?
(ii) direction of a is along AB?
View Solution

