A solid sphere of mass 3kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface? (in N)
The correct Answer is:20
F+f=ma ………..i
Torque equation about point of contact
F2R=IPα
F2R=(25mR2+mR2)α
F=710mRα………….ii
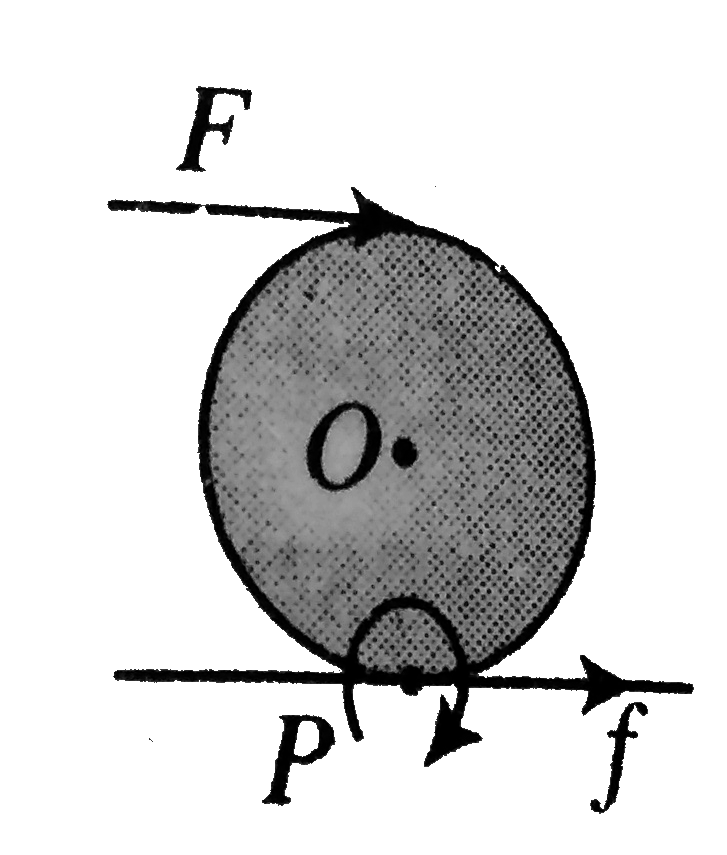
From no sliding case a=Rα………….iii
From ii and iii a=10F7m.........iv
From i and iv F+f=m.107Fm⇒f=37F
i.e friction will act in backwad direction. For no sliding
f≤μN
37F≤μmg⇒f≤73mmg
f≤73×27×3×10⇒F≤20N
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere of masss 0.50 kg si kept on a horizontal surface. The coeffici8ent of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
View SolutionA heavy box of mass 20 kg is pulled on a horizontal force.If the coefficient of kinetic friction between the box and the horizontal surface is 0.25, find the force of friction exerted by horizontal surface on the box.
View Solution
Knowledge Check
A solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmgA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmgA rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
A5 NB10 NC12 ND20 N
A block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of mass 70 kg is kept on a rough horizontal surface and coefficient of static friction between block and surface is 0.4 . A man is trying to pull the block by applying a horizontal force .The net contact force exerted by the surface on the block is F , then:
View SolutionA body of mass m kept on the floor of a lift moving downwards is pulled horizontally. If μ is the coefficient of friction between the surface in contact, then
View Solution
