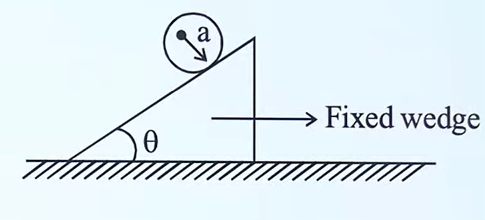
Statement I: A disc is allowed to roll purely on an inclined plane as shown in Fig. A force F parallel to the incline and passing through the centre of the disc acts which remains constant during the motion.
It is possible that for certain values of F, the friction on the disc is acting along downward direction and for certain other values of F, the friction on the disc be acting along upward direction and there is no other possibility.
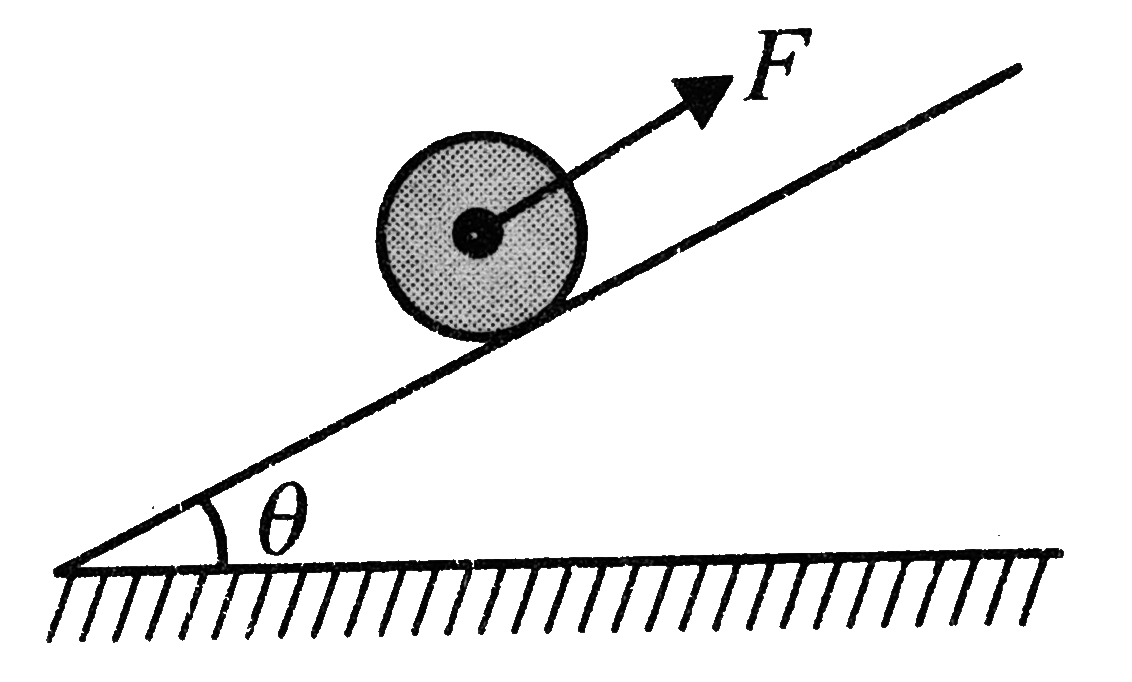
Statement II: The friction (if acting) will be static and not kinetic in nature.
Statement I is True, Statement II is True, Statement ll is a correct explanation for Statement I.
Statement I is True, Statement II is True, Statement II is NOT a correct explanation for Statement I
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:D
If F>mgsinθ, then friction on disc will be in downward directon and if F<mgsinθ, then friction on disc will be in upward direction. If F=mgsinθ, then no friction will act on disc. Hence, Statement I is false.
Statement II is true because in pure rolling, friction can be either static or no friction.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
The value of F at which no friction will act on block on inclined plane , is :
A2μmgB2μmg+2m>anθC2μmg+m>anθD2μmg+mgsinθA disc roll on an inclined plane without slipping Rotational and total energy is
A3:1B1:3C√3:1D0:1A disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
A76B54C32Ddepends on angle of inclination
The acceleration of a disc rolling (purely) down an inclined plane of inclination θ is given as a=xg(sinθ)3 .Find x
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View SolutionA disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
View Solution