The motion of a sphere moving on a rough horizontal surface changes from pure sliding (without rolling) to pure rolling (without slipping). In this process, the force of friction
(i) intially acts opposite to the direction of motion and late in the direction of motion
(ii) cause linear retardation
(iii) causes angular acceleration
(iv) stops acting when pure rolling begins
initially acts opposite to the direction of motion and later in the direction of motion
causes linear retardation
causes angular acceleration
stops acting when pure rolling begins
The correct Answer is:B, C, D
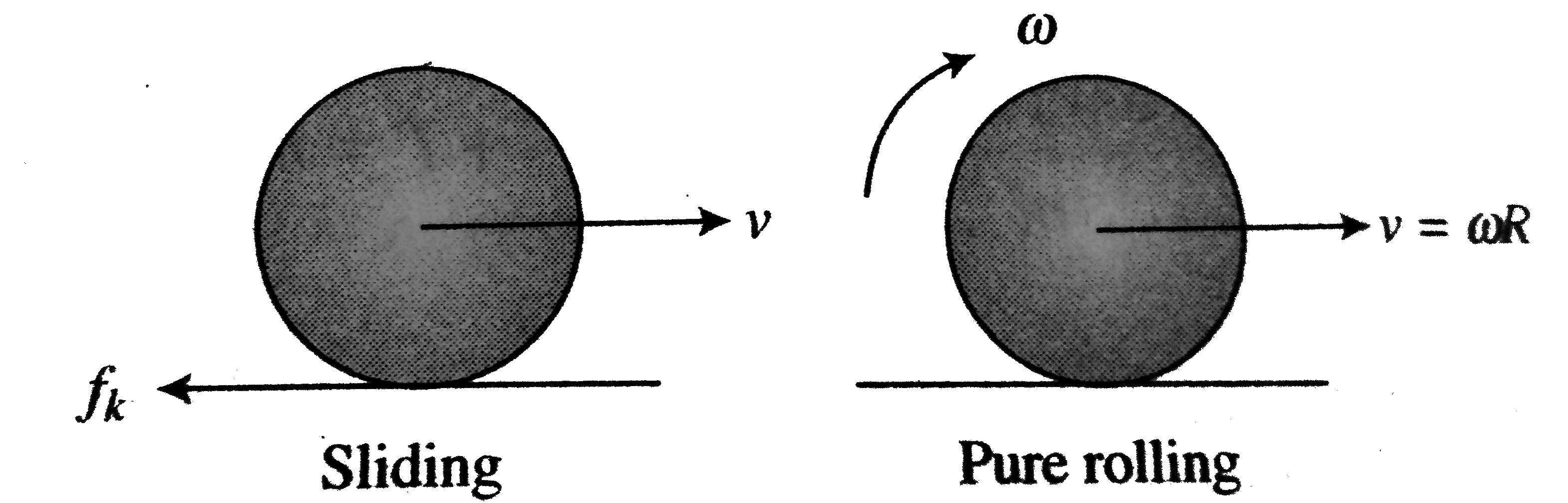
fk is opposite v it causes linear retardation. But fk produces clockwise torque about centre which gives angular acceleration. When pure rolling starts, friction stops acting because bottom point has no tendency to slip.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A disc is in pure rolling motion on a rough horizontal surface. It enters into a frictionless horizontal surface. What will happen?
View SolutionA solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View Solution
Knowledge Check
A solid homogeneous sphere is moving on a rough horizontal surface, partily rolling and partly sliding. During this kind of motion of the sphere.
Atotal kinetic energy of the sphere is conserved.Bangular momentum of the sphere about any point on the horizontal surface is conservedConly the rotational kinetic energy about the centre of mass is conservedDnone of the aboveA solid homogenous sphere of mass M and radius r is moving on a rough horizontal surface, partly rolling and partly sliding. During this kind of motion of this sphere
Atotal kinetic energy is conservedBthe angular momentlim of the sphere about the point of contact with the plane is conservedConly the rotational kinetic energy about the centre of mass is conservedDangular momentum about the centre of mass of conserved.A solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
Atotal kinetic energy is conservedBthe angular momentum of the sphere about the point contact with the plane is conservedConly the rotational kinetic energy about the centre of mass is conservedDangular momentum about the centre of mass is conserved
A solid sphere is thrown up a rough incline. The sphere rolls up without slipping and eventually comes down rolling without slipping. The direction of friction during upward and downward motion respectively is :-
View SolutionWhen a person walks on a rought surface, the frictional force exerted by surface on the porson is opposite to the direction of his motion.
It is the force exerted by the road on the person that causes the motion.
View SolutionA heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
View SolutionAssertion : A sphere is placed in pure rolling condition over a rough inclined surface.Then, force of friction will act in downward direction

Reason : Angular acceleration (actually retardation) due to friction is anti-clockwise.
View SolutionA cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the frictional force acting on the cylinder are.
View Solution
