AB is a horizontal diameter of a ball of mass m=0.4kg and radius R=0.10m. At time t=0, a sharp impulse is applied at B at angle of 45∘ with the horizontal as shown in figure so that the ball immediately starts to move with velocity v0=10ms−1

a. Calculate the impulse and angular velcity of ball just after impulse provided.
If coefficient of kinetic friction between the floor and th ball is μ=0.1. Calculate. The
b. velocity of ball when it stops sliding,
c. time t at that instant
d. horizontal distance travelled by the ball up to that instant.
e. angular displacement of the ball about horizontal diameter perpendicular to AB, up to that instant, and
f. energy lost due to friction (g=10ms−2)
Since, line of action of impulse does not pass through centre of mass of the sphere, therefore, just after application of impulse, the sphere starts to move, both translationally and rotationally. Translation motion is produced by horizontal component of the impulse, while rotational motion is produced by momnt of the impulse. Let the impulse applied be J.
Then its horizontal coponent provides horizontal motion.
J.cos45∘ which gives J=4√2kgms−1
Moment of inertial of ball about centroidal axis is
I=24mR2=1.6×10−30kgm2
Initial angular moment of ball (about centre) =J(Rsin45∘)
Angular impule will change angular momentum of the ball.
J.Rsin45∘=△L=(Iω0−0)
Which gives ω0=250rads−1(clockwise)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionThree identical balls eah of mass m=0.5 kg are connected with each other as shown in figure and rest over a smooth horizontal table At moment t=0, ball B is imparted a horizontal velocity v0=9ms−1 calculate velocity of A just before it collides with ball C.
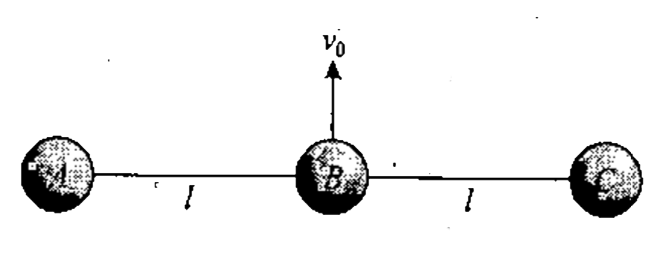
View Solution
Knowledge Check
A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is
 A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2Ns
A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2NsA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
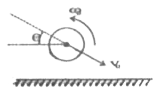 AdecraseBincreaseCremains constantDnone of these
AdecraseBincreaseCremains constantDnone of theseA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
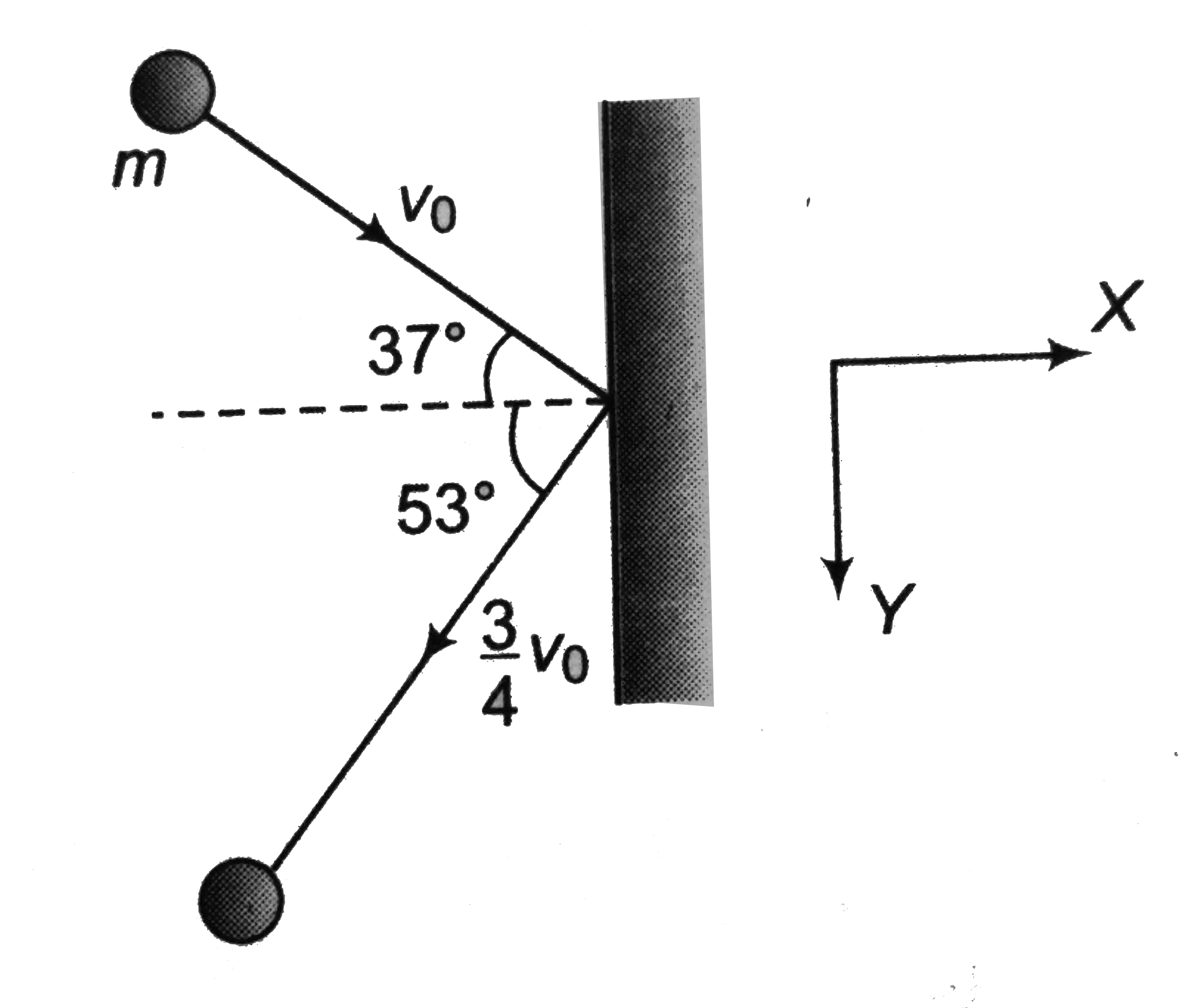 A−m2v0ˆjB−34mv0ˆiC−54mv0ˆiDNone of the above
A−m2v0ˆjB−34mv0ˆiC−54mv0ˆiDNone of the above
A ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor with velocity v0=10ms−1 towards a smooth vertical wall if coefficient of restitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter) I=0.0125kgm2. The balls rolls with velocity V0=10ms−1 towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7, velocity V of the ball after the collision is (g=0ms−2)
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
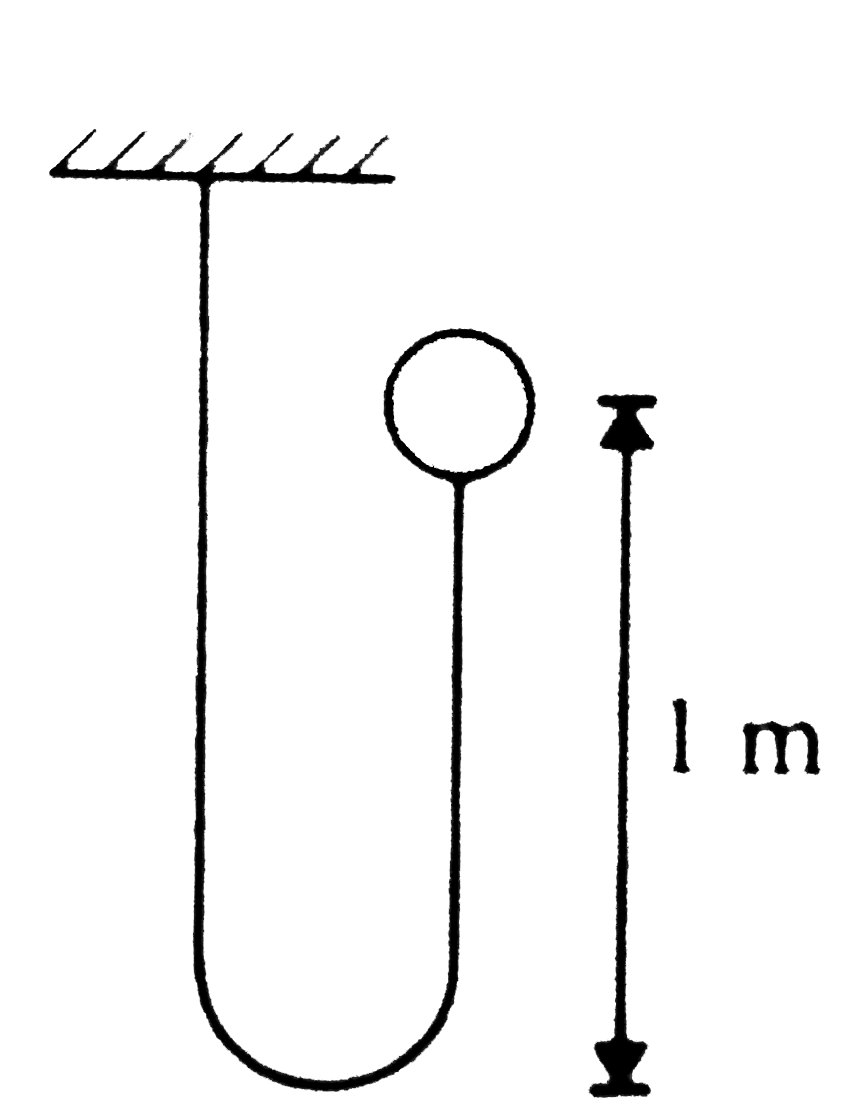
View SolutionA ball of mass 0.1 kg is thrown against a wall. It strikes the wall normally with a velocity of 30 ms−1 and rebounds with a velocity of 20 ms−1. Calculate the impulse of the force exerted by the wall.
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View Solution
