A wheel of radius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shown in figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. initially, the wheel is rotating at a speed ω in direction such that the block slides up the plane. How far will the block move before stopping?
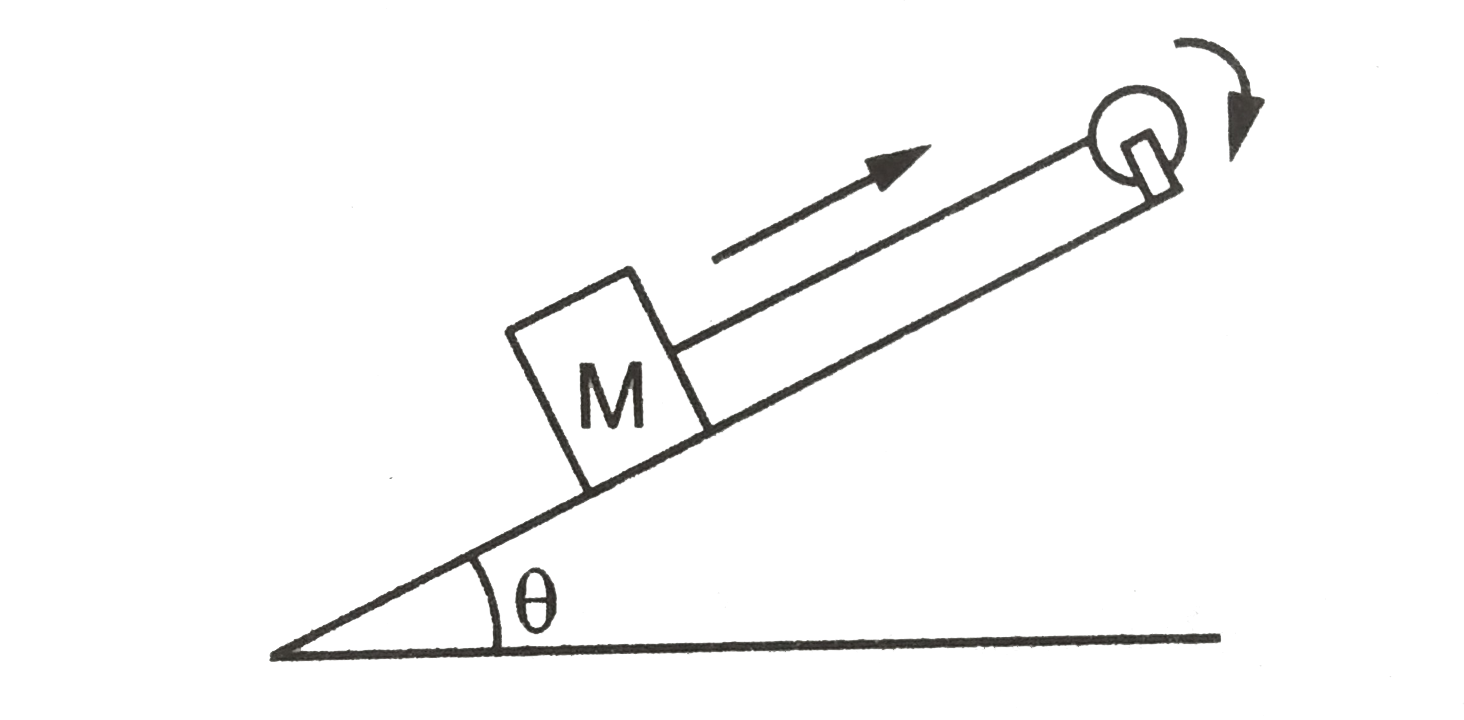
Suppose the deceleration of the block is a. The linear deceleration of the rim of the wheel is also a. the angular deceleration of the wheel is α=ar. If the tension in the string is T,the equations of motion are as follows:
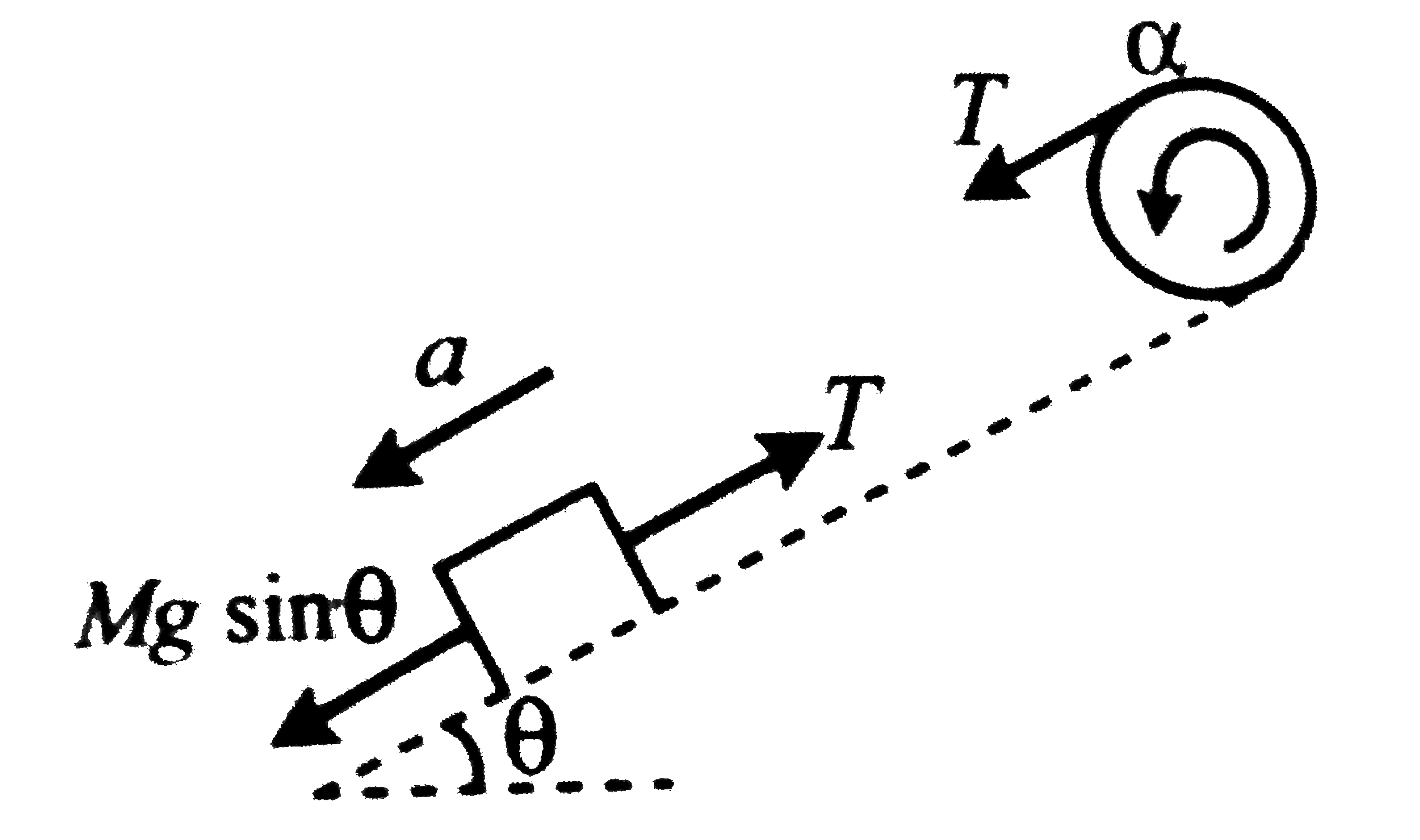
Mgsinθ=T=Ma and Tr=Iα=Iar
Elinating T from these equations
Mgsinθ−Iar2=Ma
⇒a=Mgr2siθ(I+Mr2)
The initial velocity of the block up the incline is v=ωr. Thus the distance moved by the block before stopping is
x=v22a=ω2r2(I+Mr2)2Mgr2siθ−(I+Mr2)ω22Mgsinθ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Subjective
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Single Correct
Explore 97 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.3
Explore 15 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
A wheel of rdius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shownin figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. INitialy, tehwheel is rotating at a speed ω in direction such that the block slides pu the plane. How far wil the block move before stopping?

View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
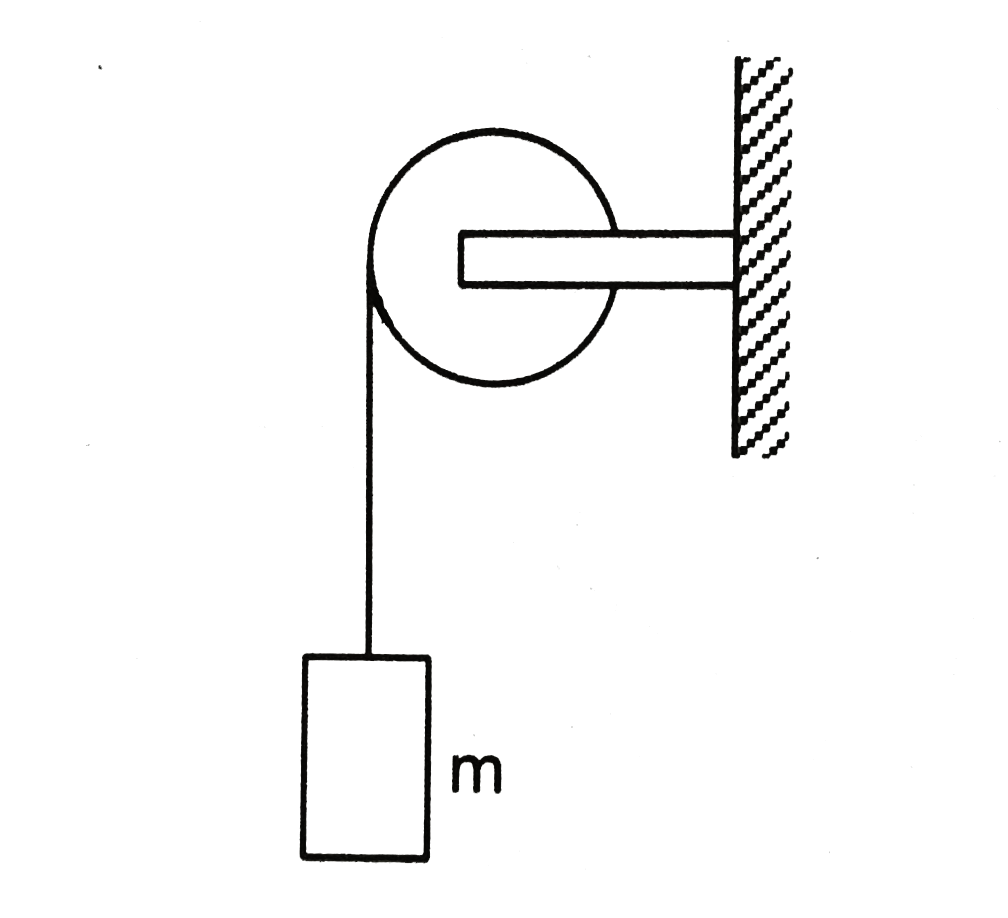
View Solution
Knowledge Check
A block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
AmgBmgcosθCmgsinθDmgtanθA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
 Athe centre of mass of sphere accelerates upwards.Bthe centre of mass of shpere accelerates downwardsCthe lowest point of contact accelerates upwards.Dthe lowest point of contect accelerates downwards.
Athe centre of mass of sphere accelerates upwards.Bthe centre of mass of shpere accelerates downwardsCthe lowest point of contact accelerates upwards.Dthe lowest point of contect accelerates downwards.An cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
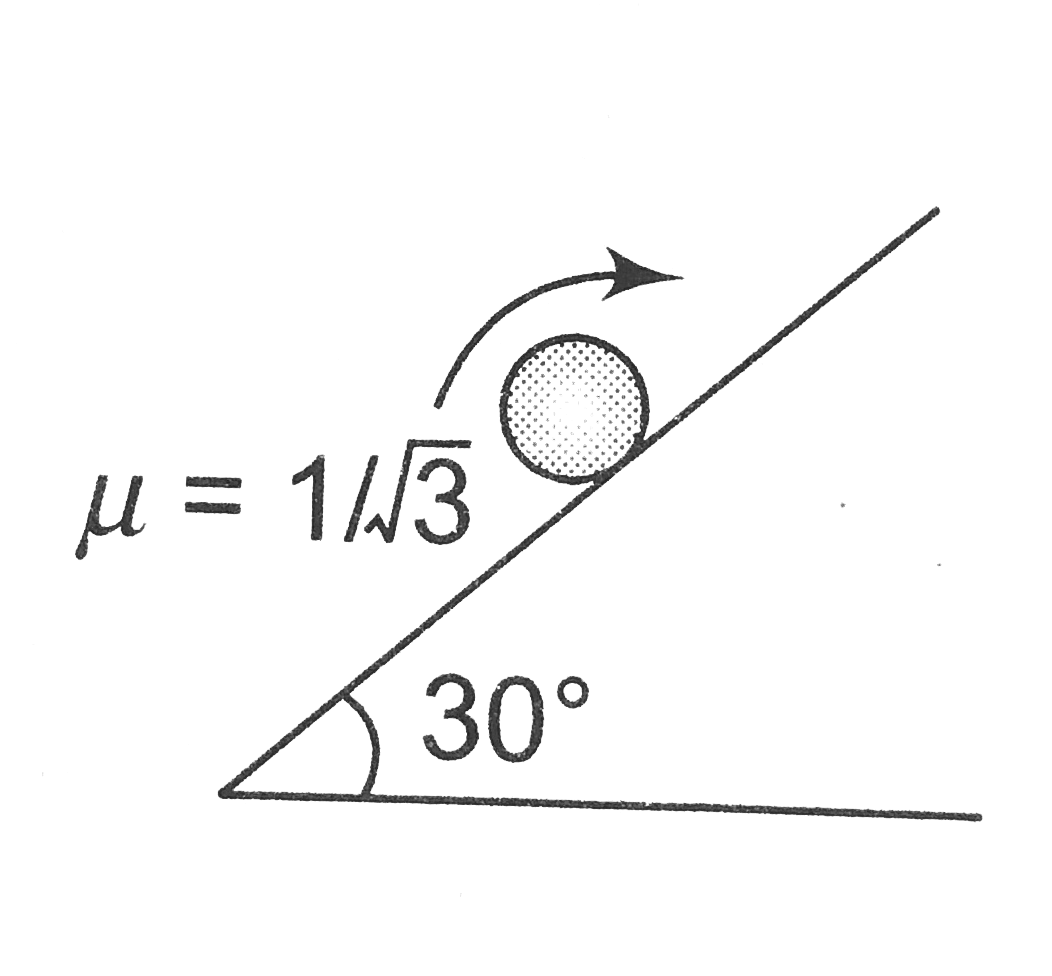 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
A wheel having moment of inertia 2 kig m^2 about its xis, rotates at 50 rpm about this axis. Find the torque that can stop the wheel in one minute.
View SolutionA block is about to slide down an inclined plane when its inclination to the horizontal is θ. If now a 5 kg weight is attached on the block :
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA wheel of mass M and radius a and M.I. IG (about centre of mass) is set rolling with angular velocity ω up a rough inclined plane of inclination theta. The distance traveled by it up the plane is
View SolutionA wheel whose radius is R and moment of inertia about its own axis is I, rotates freely about its own axis. A rope is wrapped on the wheel. A body of mass m is suspended from the free end of the rope. The body is released from rest. The velocity of the body after falling a distance h would be:
View Solution

